Question

A ball is dropped from height $5m$. The time after which ball stops rebounding if coefficient of restitution between ball and ground $e=1/2$ is:
a) $1\sec $
b) $2\sec $
c) $3\sec $
d) $infinite$

Answer 1

Hint: The ball will hit the ground and will bounce back to a smaller height. It will again hit the ground and bounce off to an even smaller height. This process goes on for some time and the ball comes to rest. We will use this concept to find the solution to the problem.

Formula used:
$T={{t}_{1}}+{{t}_{2}}+{{t}_{3}}+......$
${{t}_{1}}=\dfrac{{{v}_{1}}}{g}$
${{v}^{2}}-{{u}^{2}}=2aS$

Complete answer:
The ball will drop on the ground several times before it comes to rest. We will derive a general formula and then put the respective parameters’ value in them at the last to obtain the answer.
Let the ball be initially dropped from a height of ${{h}_{1}}$. Let the ball take time ${{t}_{1}}$ to reach the ground. The ball bounces off the ground and achieves a height of ${{h}_{2}}$. It takes time ${{t}_{2}}$ to reach from that height to ground. And similarly, the process goes on. This can be easily understood using the diagram as:

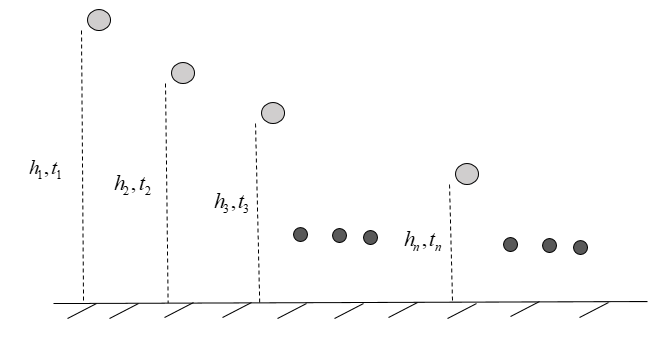
We know that the time taken by the ball to reach the rest position $(T)$ is given by:
$T={{t}_{1}}+{{t}_{2}}+{{t}_{3}}+......$ ------(i)
It forms an infinite series.
Also, we know that the time taken by the ball to reach the ground during first fall is given by:
${{t}_{1}}=\dfrac{{{v}_{1}}}{g}$ -------(ii)
Where, ${{v}_{1}}$ is the velocity of the ball just before collision and $g$ is the acceleration due to gravity.
Here, ${{v}_{1}}$ can be found using the equation:
${{v}^{2}}-{{u}^{2}}=2aS$
Here, the initial velocity is zero. Hence, ${{v}_{1}}$ can be given as:
${{v}_{1}}=\sqrt{2g{{h}_{1}}}$ ------(iii)
We know that further time periods, i.e., ${{t}_{2}},{{t}_{3}},{{t}_{4}},...$, are related to the first time of fall, i.e., ${{t}_{1}}$, through the coefficient of restitution. This relation is given by:
${{t}_{2}}=e{{t}_{1}}$
${{t}_{3}}={{e}^{2}}{{t}_{1}}$
${{t}_{4}}={{e}^{3}}{{t}_{1}}$
.
.
.
We will put these relations in equation (i), we get:
$T={{t}_{1}}+e{{t}_{1}}+{{e}^{2}}{{t}_{1}}+{{e}^{3}}{{t}_{1}}+......$
$\Rightarrow T={{t}_{1}}(1+e+{{e}^{2}}+{{e}^{3}}+......)$
Thus, this forms a G.P. Using the summation formula for G.P., we can write:
$\Rightarrow T={{t}_{1}}\left( \dfrac{1}{1-e} \right)$
Using equation (ii), replacing ${{t}_{1}}$:
$\Rightarrow T=\left( \dfrac{{{v}_{1}}}{g} \right)\left( \dfrac{1}{1-e} \right)$
Using equation (iii), we can replace ${{v}_{1}}$ as:
$\Rightarrow T=\left( \dfrac{\sqrt{2g{{h}_{1}}}}{g} \right)\left( \dfrac{1}{1-e} \right)$
$\Rightarrow T=\left( \sqrt{\dfrac{2{{h}_{1}}}{g}} \right)\left( \dfrac{1}{1-e} \right)$
Now, putting the values of the parameters in the equation, we get:
$\Rightarrow T=\left( \sqrt{\dfrac{2\times 5}{9.8}} \right)\left( \dfrac{1}{1-0.5} \right)$
$\Rightarrow T\simeq 2\sec $
Hence, the answer is $2\sec $ and the correct option is (b).

Note: Here, we need to find the appropriate parameter to form the G.P. In this question, the G.P. formed is in time. Forming a G.P. in other parameters would have taken more time to form as well as to execute. In the questions where there is a series of bounces or a series of any other parameters, it tends to form a geometric progression.