JEE Advanced 2025 Revision Notes for Physics on Modern Physics

Cathode Rays

• The stream of negatively charged particles moving from the cathode to the anode in a discharge tube is known as cathode rays.
  
  

Properties of Cathode Rays

• The following are some of the properties of cathode rays. 

1. Cathode rays follow a straight path.

2. The material on which cathode rays fall heats up.

3. Cathode rays have the ability to cause physical and chemical changes, as well as exert mechanical pressure.

4. Cathode rays have the ability to ionise gases and produce X-rays.

5. Fluorescence can be produced by cathode rays.

6. Cathode rays are capable of penetrating thin metal foils.

7. In an electric and magnetic field, cathode rays are deflected.

8. Negative charge is carried by cathode rays.

Motion of Cathode Rays (Electrons) Parallel in Electric Field

• An electron has mass $(m)$ and charge$(e)$. It moves in an electric field$(E)$. Then,

1. Then, force on electron, $F=eE$

2. An electron's path is a linear line when it is projected in the direction of the electric field or in the opposite direction.

3. Electric field intensity, $E=\dfrac{V}{d}=\dfrac{\text{ potential between plates }}{\text{ distance between plates }}$

4. Acceleration applied to electrons,$a=\dfrac{F}{m}=\dfrac{eE}{m}$
   
   

Motion of Cathode Rays (Electron) Perpendicular to Electric Field

• An electron has mass $(m)$ and charge $(e)$. It enters into the electric field perpendicularly. Then,

1. Then, force on the electron, $F=eE$.

2. After covering the length $(l)$, deviation of electron, $y=\dfrac{1}{2}a{{t}^{2}}=\dfrac{1}{2}\left( \dfrac{eE}{m} \right){{\left( \dfrac{l}{{{v}_{x}}} \right)}^{2}}$then, the electron's path is parabolic.

3. If the vertical component of electron velocity ${{v}_{x}}$, then ${{v}_{x}}=at=\left( \dfrac{eE}{m} \right)t=\left( \dfrac{V}{d} \right)\left( \dfrac{e}{m} \right)\left( \dfrac{l}{{{v}_{x}}} \right)$

4. Resultant velocity, $v=\sqrt{v_{x}^{2}+v_{y}^{2}}$ and $\theta ={{\tan }^{-1}}\left( \dfrac{{{v}_{y}}}{{{v}_{x}}} \right)$

Uses of Cathode Rays

1. In a cathode ray oscilloscope.

2. In production of X-rays.

Positive Rays

• Positive rays move positive ions in the discharge tube filled with gas. 

• These particles have a mass that is nearly equal to that of gas atoms.
  
  

Positive Rays Were Discovered by Goldstein.

Below are some of the properties of positive rays.

1. These are positively charged particles that move quickly.

2. In a magnetic field, these rays are deflected.

3. In an electric field, these rays are deflected.

4. The rays follow a straight path.

5. Positive rays travel at a slower rate than cathode rays.

6. These rays have the potential to damage the photographic plate.

7. These rays pass through the thin aluminium foil without being absorbed.

8. Fluorescence and phosphorescence can be produced by these rays.
   
   

Matter Wave

• Some phenomena, such as diffraction and interference, can be explained in terms of light's wave character. 

• Other phenomena, such as black body radiation and the photoelectric effect, can only be explained in terms of their particle nature.

• Then, light is said to have two personalities. Einstein conducted such studies on light waves in 1905.

• In 1942, Louis-de-Broglie extended the concept of photons to material particles such as electrons, proposing that matter has both a wave and a particle nature.

De-Broglie Relation

A wave, according to de-Broglie, is a moving particle of energy. De-Broglie waves, also known as matter waves, are these waves.

• The energy of a photon, according to quantum theory, $E=h\nu...\text{(i)}$

• If mass of the photon is taken as $m$, then as per Einstein's equation,

• $E=m{{c}^{2}}$……(ii)

• From Eqs. (i) and (ii), we get $hv=m{{c}^{2}}$

• $h\dfrac{c}{\lambda }=m{{c}^{2}}$$[\because \nu=c/\lambda ]$

Here , $\lambda =$ wavelength of photon $\lambda =\dfrac{h}{mc}$

• The above equation, according to de-Broglie, is completely general and applies to photons as well as all other moving particles.

• Then, $\lambda =\dfrac{h}{mv}=\dfrac{h}{\sqrt{2mE}}$

• Here, $m$ is mass of particle and $v$ is its velocity

Properties of Matter Wave

• The following are some of the properties of matter waves. 

1. De-Broglie wavelength, $\lambda \propto \dfrac{1}{v}$. The wavelength will be smaller if the particle moves faster, and vice versa.

2. When the particle is at rest$(v=0)$, then the de-Broglie wavelength is infinite$(\lambda =\infty )$. Such a wave cannot be visualised.

3. Electromagnetic waves are produced by charged particle motion, so De-Broglie waves cannot be electromagnetic.

4. A region of uncertainty is defined by the wavelength of a wave associated with a moving particle, within which the location of the particles is unknown.

Photoelectric Effect

• The photoelectric effect is the phenomenon of electrons being emitted from a metal surface by the action of light rays; the emitted electrons are called photoelectrons, and the current produced by these electrons is called photoelectric current.

• The photoelectric effect is based on the law of energy conservation.

• The photons vanish completely in the photoelectric effect, and all of their energy is transferred to the photoelectrons.

• The absorption of one photon corresponds to the emission of one electron.

• Because photons can be involved in a variety of ways, the ratio of electrons emitted to photons incident is less than unity.

Laws of Photoelectric Effect

• There is no time lag between electron emission and light incidence.

• The intensity of incident light has a direct relationship with the number of emitted electrons.

• The kinetic energy of emitted electrons is independent of incident light intensity.

• The kinetic energy of emitted electrons is proportional to the incident light frequency.

• The number of emitted electrons is independent of incident light frequency.

• If the incident light frequency is less than the threshold frequency, no electron is ejected. 

• Photoelectric emission is a one-time event. The time lag between the incidence of radiation and emission of photoelectrons is very small, or less than even ${{10}^{-9}}$ second.

Threshold Frequency

• The threshold frequency or cut-off frequency $\left( {{\nu}_{0}} \right)$ is the lowest frequency of light required to eject electrons from a metallic surface. 

• Even if the intensity is high, no photoelectric emission is possible at a frequency lower than the cut-off frequency.

Work Function

• The work function of metal is the minimum energy required to eject electrons from metal (W)

• $W=h{{\nu}_{0}}\quad \left[ \begin{array}{*{35}{l}}\text{ where, }h=\text{Planc{k}'sconstant}  \\\text{ and }\quad {{\nu}_{0}}=\text{ threshold frequency }  \\\end{array} \right]$

Einstein's Equation of Photoelectric Effect

• Kinetic energy, ${{E}_{K}}=h\left( \nu-{{\nu}_{0}} \right)$

$\Rightarrow \quad \dfrac{1}{2}m{{v}_{{{\max }^{2}}}}=h\left( \nu-{{\nu}_{0}} \right)$

• Or $\dfrac{1}{2}m{{v_{max}}^{2}} =h\nu-h{{\nu}_{0}}\quad \left[ \because W=h{{\nu}_{0}} \right]$ or $\quad \dfrac{1}{2}m{{v}_{{{\max }^{2}}}}=h\nu-W$

Here, ${{E}_{K}}=$ maximum kinetic energy of photoelectron, $\nu=$ Frequency of incident light, ${{\nu}_{0}}=$ Threshold frequency, $h=$ Planck's constant And $W=$ work function

Relation Between Stopping Potential and Threshold Frequency

• All kinetic energy will be converted to potential energy if an electron is retarded by a potential difference of ${{V}_{0}}$.

$\Rightarrow e{{V}_{0}}={{K}_{\max }}=\dfrac{1}{2}m{{v}_{{{\max }^{2}}}}=h\text{v}-h{{v}_{0}}=h\text{v}-W\quad \left[ \because W=h{{v}_{0}} \right]$ 

Here , ${{V}_{0}}$ is called stopping potential

Photoelectric Cell

• It is a device that converts light energy directly into electric energy using the photoelectric effect. These are of three types

1. Photo emissive cell

2. Photovoltaic cell

3. Photoconductive cell

As we know that Saturation current in the photocell varies with distance as $i\propto \dfrac{1}{{{d}^{2}}}$.

Applications of Photoelectric Cells

• In the cinema, television, and photo telegraphy, sound reproduction.

• When it comes to determining the temperature of celestial bodies.

• To keep the temperature in the furnace and the chemical process under control.

• Automatic doors are used.

• Photoelectric counters are a type of photoelectric counter.

• In automatic street light switches.

• Photoelectric sorters are used for this.

• In space, to obtain electrical energy from sunlight while travelling through space,$v\ge {{v}_{0}}$ or $\lambda \le {{\lambda }_{0}}$.

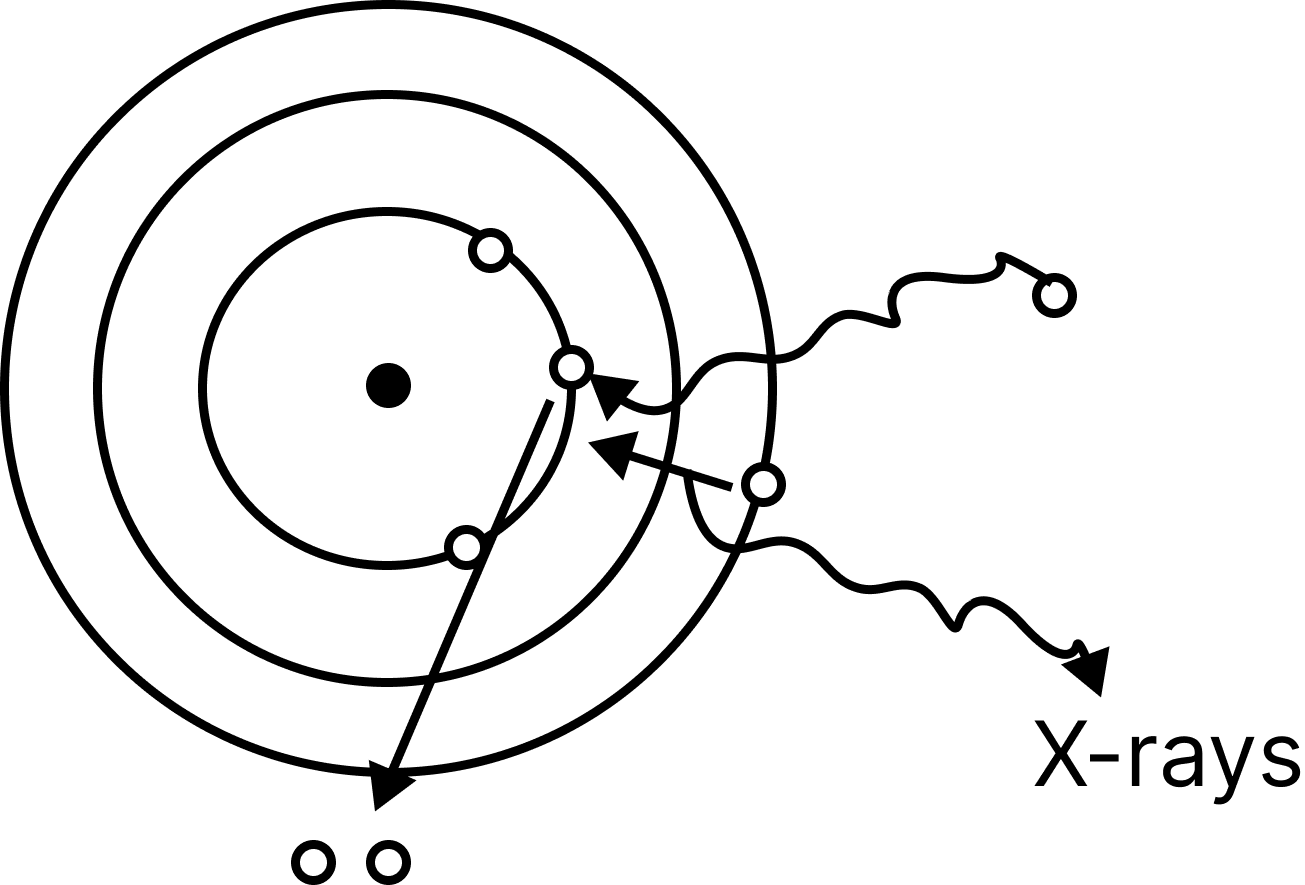
X-rays

• When fast moving cathode rays collide with a metal piece with a high melting point and mass number, invisible rays are produced. X-rays are the name for these rays.
  
  

x-rays

• Roentgen was the first to discover these rays. The nature of these rays is electromagnetic. 

• The Coolidge tube is the device that produces X-rays.

Properties of X-rays

• The following are some of the properties of X-rays. 

1. The nature of these is electromagnetic.

2. X-rays travel at the speed of light in a straight line.

3. Reflection, refraction, interference, diffraction, and polarisation are all shown here. 

4. Wavelength of X-rays is the order of one angstrom.

5. Electric and magnetic fields have no effect on them.

6. When these fall on fluorescent substances, they produce light.

7. X-rays ionise the gas they pass through.

8. X-rays penetrate different substances at different depths.

9. The photoelectric effect can be seen in X-rays.
   
   

Applications of X-rays

• X-rays used in surgery In radiotherapy

• X-rays used in trading - In laboratory

• X-rays used in searching

Moseley's Law

• The frequency of an X-ray spectrum line is proportional to the number of atoms in the element. $v\propto {{(Z-b)}^{2}}$ or $v=a{{(Z-b)}^{2}}$

• Here , $a$ and $b$ are constants and $Z$ is replaced by $(Z-b)$ due to the screening atomic number effect of orbital electrons $a=\dfrac{m{{e}^{4}}}{8\varepsilon _{0}^{2}{{h}^{3}}}\left( \dfrac{1}{n_{1}^{2}}-\dfrac{1}{n_{2}^{2}} \right)$

Bragg's Law

• Bragg's law states that, when the X-ray is incident onto a crystal surface its angle of incidence $\theta $, will reflect back with the same angle of scattering $\theta$. 

• And when the path difference $d$ is equal to a whole number $n$, of wavelength$\lambda $. There will be a positive interference.
  
  

Bragg’s law

• Consider the diagram in which an X-ray beam is diffracted at an angle $\theta $, as shown in figure. Clearly, the path difference between rays 1 and 2 is significant $2d\sin \theta $.

• For maxima of X-rays diffracted from the crystal. $2d\sin \theta =n\lambda $

• Here, $n=1,2,3,\ldots ,d$ is the interatomic gap of the crystal.

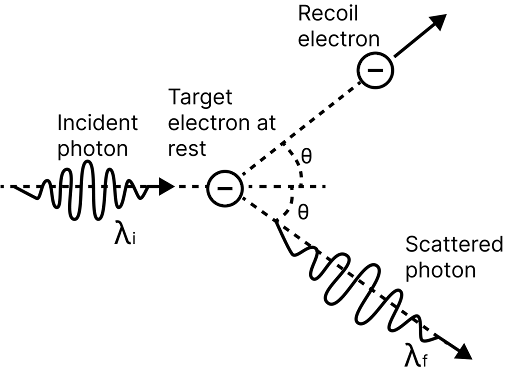
Compton Shift

• Some of the scattered X-rays have a longer wavelength than the incident X-rays when X-rays are scattered by loosely bound electrons in a target. 

• The wavelength shift is referred to as the Compton shift. The Compton Effect is a phenomenon in which the wavelength of incident X-rays increases and, as a result, the energy decreases due to scattering from an atom.

Expressions for Compton Shift

Crompton scattering

1. The wavelength shift caused by Compton is given by $\Delta \lambda =\dfrac{h}{{{m}_{0}}c}(1-\cos \phi )$ Here, $h=$ Planck's constant,${{m}_{0}}=$ Rest mass of electron, $\phi =$ Angle of scattering and $c=$ speed of light

2. Kinetic energy of recoil electron, ${{E}_{K}}=\dfrac{bc}{\lambda }=\dfrac{hc}{{{\lambda }^{\prime }}}$

3. Direction of recoil electron,$\tan \theta =\dfrac{\lambda \sin \phi }{{{\lambda }^{\prime }}-\lambda \cos \phi }$

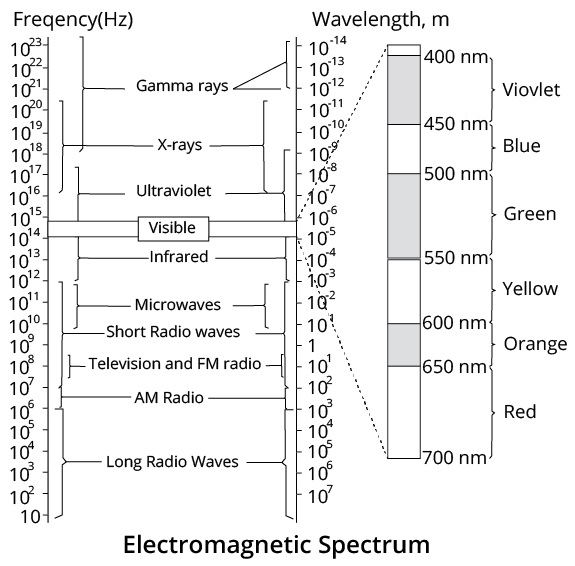
Electromagnetic Spectrum

• The systematic arrangement of electromagnetic waves in increasing or decreasing wavelength $(\lambda )$ or frequency $(v)$ is called the electromagnetic spectrum. 

• The range varies from ${{10}^{-12}}~\text{m}$ to ${{10}^{4}}~\text{m}$, i.e. from $\gamma $-rays to radio waves.
  
  

Electromagnetic Spectrum

Bohr's Model of Hydrogen

• Like Atoms

• Bohr combined classical and early quantum concepts in the form of three postulates, which are listed below.

• The first postulate is that Despite electromagnetic theory's predictions, an electron in an atom could revolve in a stable orbit without emitting radiant energy.

• Second Postulate Only those orbits in which the angular momentum is positive cause the electron to revolve around the nucleus some integral multiple of $h/2\pi $, where $h$ is Planck's constant.

• The angular momentum, $L=\dfrac{n\cdot h}{2\pi }$ , $mvr=\dfrac{nh}{2\pi }\quad (\because L=mvr)$ Here, $n=1,2,3,\ldots $

• Third Postulate An electron may change from one of its specified non-radiating orbits to a lower-energy orbit. When this happens, a photon with the same energy as the energy difference between the initial and final states is emitted. The expression of it is,

$h\text{v}={{E}_{i}}-{{E}_{f}}$

Here, ${{E}_{i}}$ and ${{E}_{f}}$ are the energies of the initial and final states and ${{E}_{i}}>{{E}_{f}}$.

Condition of Circular Orbit

• The central nucleus of the atom contains the entire positive charge and almost all of the atom's mass. 

• The coulomb attraction between the electron and the nucleus provides the necessary centripetal force for circular orbits.

$\dfrac{m{{v}^{2}}}{r}=\dfrac{1}{4\pi {{\varepsilon }_{0}}}\dfrac{Z{{e}^{2}}}{{{r}^{2}}}$ 

• Condition for quantization, $mvr=\dfrac{nh}{2\pi }$. Radius of nth orbit (from above two equations)${{r}_{n}}=\dfrac{{{\varepsilon }_{0}}{{h}^{2}}{{n}^{2}}}{\pi mZ{{e}^{2}}}=0.53\dfrac{{{n}^{2}}}{Z}{A^o}=\dfrac{{{n}^{2}}}{Z}{{r}_{0}}$

• Here, ${{r}_{0}}=0.53\,A^o$ Size of an atom is approx. $1\,A^o$. Speed of electron in $n$th orbit, ${{v}_{n}}=\dfrac{{{e}^{2}}}{2{{\varepsilon }_{0}}h}\dfrac{Z}{n}=\dfrac{c}{137}\dfrac{Z}{n}\quad $ (Here, $c=$ speed of light)

• $\text{KE}$ is ${{E}_{K}}=\dfrac{1}{4\pi {{\varepsilon }_{0}}}\cdot \dfrac{Z{{e}^{2}}}{2r}$

• $\text{PE}$ is $U=-\dfrac{1}{4\pi {{\varepsilon }_{0}}}\cdot \dfrac{Z{{e}^{2}}}{r}$

• Total energy $=-\dfrac{1}{4\pi {{\varepsilon }_{0}}}\cdot \dfrac{Z{{e}^{2}}}{2r}$

• Condition of transition, $b\text{v}={{E}_{1}}-{{E}_{2}}$

• Frequency of emitted radiation is $\text{v}=\dfrac{{{E}_{1}}-{{E}_{2}}}{b}={{Z}^{2}}Rc\left( \dfrac{1}{n_{1}^{2}}-\dfrac{1}{n_{2}^{2}} \right)$

• Wave number,$\bar{v}=\dfrac{1}{\lambda }=R{{Z}^{2}}\left( \dfrac{1}{n_{1}^{2}}-\dfrac{1}{n_{2}^{2}} \right)$
  
  

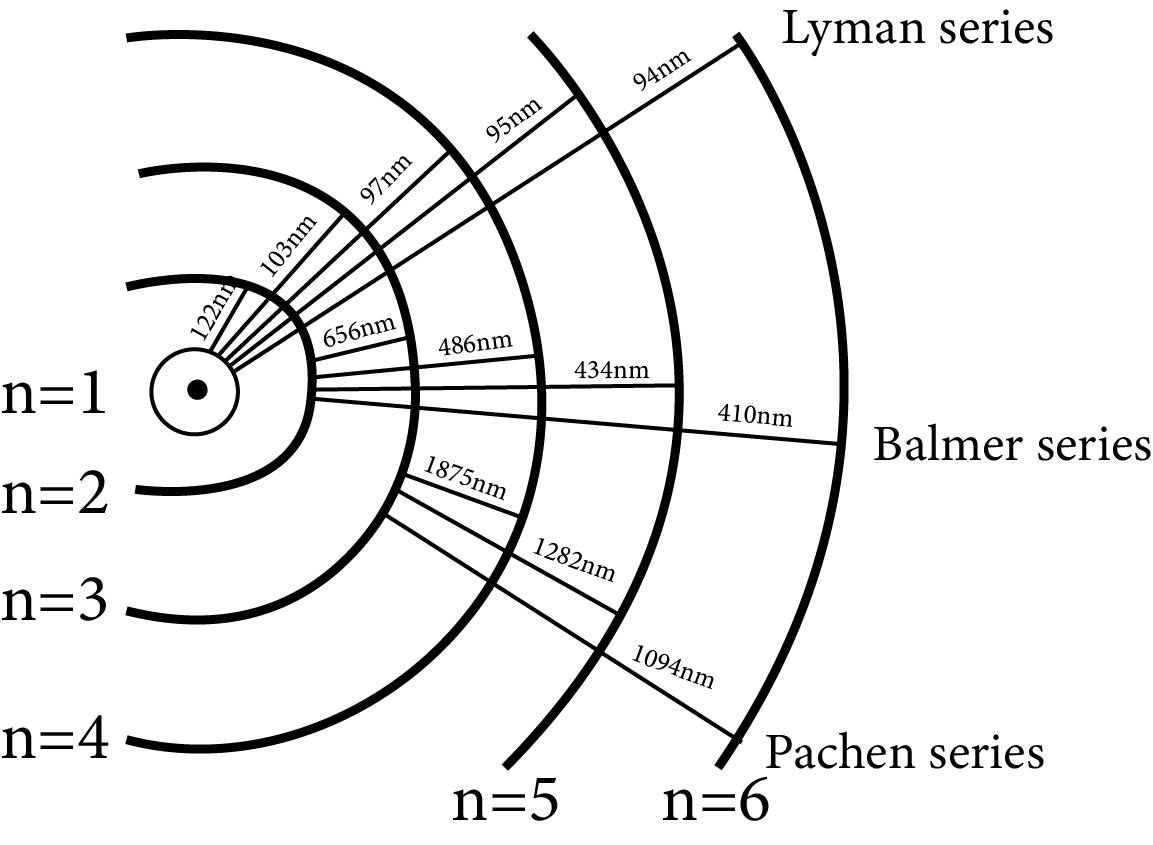
Series

Series

• The atomic hydrogen emits a spectrum that is divided into several series. 

• A difference of two terms can be used to express the frequency of a line in a series

1. Lyman series $\dfrac{1}{\lambda }=R\left( \dfrac{1}{{{1}^{2}}}-\dfrac{1}{{{n}^{2}}} \right)$, where $n=2,3,4,5,\ldots $ (ultraviolet region)

2. Ballmer series $\dfrac{1}{\lambda }=R\left( \dfrac{1}{{{2}^{2}}}-\dfrac{1}{{{n}^{2}}} \right)$, where $n=3,4,5,6,\ldots $  (Visible region)

3. Panchen series $\dfrac{1}{\lambda }=R\left( \dfrac{1}{{{3}^{2}}}-\dfrac{1}{{{n}^{2}}} \right)$, where $n=4,5,6,7,\ldots $

4. Brackett series $\dfrac{1}{\lambda }=R\left( \dfrac{1}{{{4}^{2}}}-\dfrac{1}{{{n}^{2}}} \right)$, where $n=5,6,7,8,\ldots $ ] (infrared region)

5. Pound series $\dfrac{1}{\lambda }=R\left( \dfrac{1}{{{5}^{2}}}-\dfrac{1}{{{n}^{2}}} \right)$, where $n=6,7,8,9,\ldots $ (infrared region)
   

Half-Life $\left(T_{1 / 2}\right)$ :- The period of time during which a radioactive substance's number of atoms is decreased to half its initial value is known as its half-life.

$T_{1 / 2}=0.693 / \lambda$

A radioactive substance's half-life is therefore inversely proportional to its radioactive decay constant.

Average Life $\left(T_{a v}\right)$ : The term "mean life" or "average life" of a radioactive substance refers to the arithmetic mean of all the atoms' lives.

$T_{a v}=$ sum of lives of all atoms / total number of atoms

The reciprocal of a radioactive substance's radioactive decay constant is equal to the substance's average life.

Relation between $T_{1 / 2}$ and $T_{a v}$:

$T_{1 / 2}=0.693 \times T_{\text {av }}$

Half-life $=0.693 \times$ average life

Alpha Decay: 

Alpha decay refers to the nuclear disintegration process that produces alpha particles. Uranium-238 is an example of an alpha decaying nucleus. U-238's alpha decay is

${ }_{92}^{238} \mathrm{U} \rightarrow{ }_{2}^{4} \mathrm{He}+{ }_{90}^{234} \mathrm{Th}$

The uranium atom $\left({ }_{92}^{238} \mathrm{U}\right)$ undergoes this nuclear transformation was transmuted into a thorium atom $\left({ }_{90}^{234} \mathrm{Th}\right)$ and emitted an alpha particle in the process. Examine the symbol for the alpha particle: ${ }_{2}^{4} \mathrm{He}$. Where does this sign come from in an alpha particle? The number of protons is represented by the lowest number in a nuclear symbol. That means the Alpha particles are always made up of two protons and two neutrons.

Beta Decay:

Beta particle emission, often known as beta decay, is another prevalent decay mechanism. A beta particle is just an electron with a high energy that is emitted from the nucleus. You may notice that we are in a logically problematic predicament here. Despite the fact that nuclei do not possess electrons, an electron is emitted from a nucleus during beta decay. A neutron is transforming into a proton as the electron is released from the nucleus. It's easy to imagine a neutron splitting into two parts, each of which contains a proton and an electron.That would be ideal for simplicity, but unfortunately, that is not the case (more on this subject will be explained at the end of this section). To make things easier, we'll think of beta decay as a neutron splitting into a proton and an electron. The proton remains in the nucleus, increasing the atomic number by one. The electron is expelled from the nucleus and becomes a radiation particle known as beta.An electron had to be allocated an atomic number and a mass number in order to be inserted into a nuclear equation and have the numbers add up correctly. The mass number ascribed to an electron is zero (0), which makes sense given that the mass number is the amount of protons plus neutrons, and an electron contains neither protons nor neutrons. An electron's atomic number is negative one (-1), which permits a nuclear equation involving an electron to balance atomic numbers. As a result, the nuclear symbol for an electron (beta particle) is

${ }_{-1}^{0}$ e or ${ }_{-1}^{0} \beta$

Thorium-234 is a nucleus that decays through beta disintegration. The nuclear equation for this beta decay is as follows:

${ }_{90}^{234} \mathrm{Th} \rightarrow{ }_{-1}^{0} \mathrm{e}+{ }_{91}^{234} \mathrm{~Pa}$

Gamma Radiation:

Gamma ray generation is frequently associated with nuclear processes of all types. In addition to the alpha particle, two gamma rays of varying energy are released during the alpha decay of U -238.

${ }_{92}^{238} \mathrm{U} \rightarrow{ }_{2}^{4} \mathrm{He}+{ }_{90}^{234} \mathrm{Th}+2_{0}^{0} \gamma$

Almost all of the nuclear reactions in this chapter release gamma rays, although for clarity, the gamma rays are not illustrated. Nuclear reactions provide far more energy than chemical ones.

Law of Radioactive Disintegration: 

The total amount of radioactive compound nuclei in the sample directly relates to the rate of radioactive decays per unit of time.

When the number of nuclei in a sample is $\mathrm{N}$ and the number of radioactive decays per unit time $\Delta \mathrm{t}$ is $\Delta \mathrm{N}$ then,

$\frac{\Delta N}{\Delta t} \propto N $

$\frac{\Delta N}{\Delta t}=\lambda N$

Here $\lambda$ is the constant of proportionality called the radioactive decay constant or disintegration constant.

Nuclear Fission:

Nuclear fission is the process by which a nucleus splits into two roughly equivalent-sized pieces.

Fission of $\mathrm{U}_{92}{ }^{235}$ by fast moving neutrons is represented as,

$n_{0}^{1}+\mathrm{U}_{92}^{235} \rightarrow \mathrm{Ba}_{56}^{141}+\mathrm{Kr}_{36}^{92}+\mathrm{N}_{0}^{1}+\mathrm{Q}$

Value of Q in this reaction is $200.4443 \mathrm{MeV}$.

Nuclear Reaction:- 

The three neutrons that were released can be slowed down in order to control the fission reaction of $\mathrm{U}_{92}{ }^{235}$. By putting them through moderators, this is accomplished. As moderators, carbon rods and heavy water can be used. A nuclear reaction is a structure in which fission occurs under regulated conditions.

Nuclear Fusion:

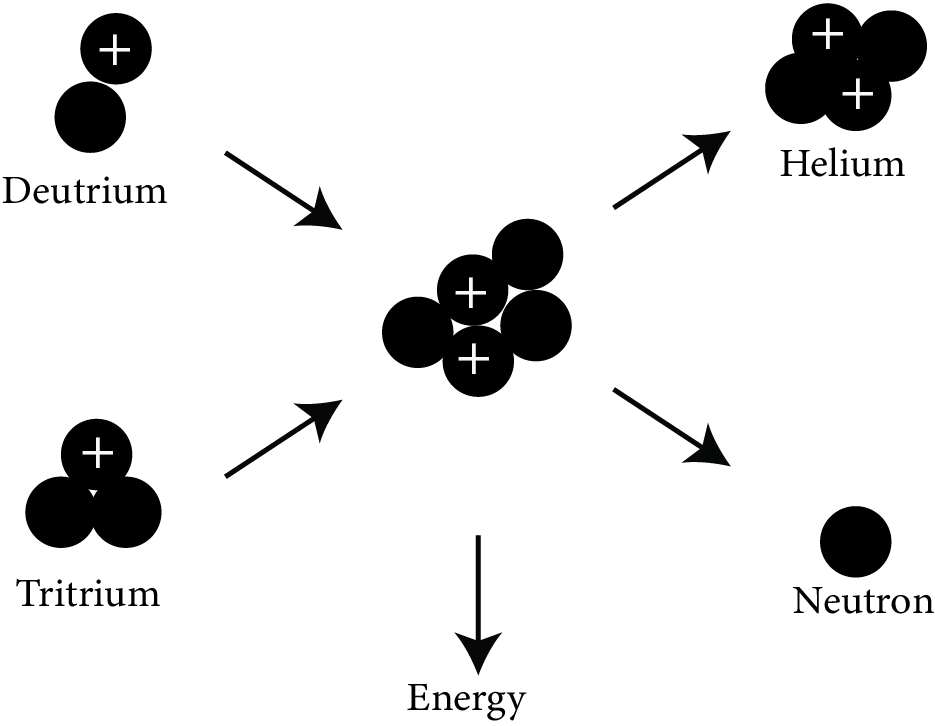
Nuclear fusion

When two lighter nuclei combine to generate a heavier nucleus, this is referred to as a fusion reaction. It is a very exothermic reaction that generates energy on a far larger scale than fission.

Fusion of four protons to produce $\mathrm{He}_{2}^{4}$ is the fusion reaction which is responsible for production of energy in the sun.

$\mathrm{H}_{1}^{1}+\mathrm{H}_{1}^{1}+\mathrm{H}_{1}^{1}+\mathrm{H}_{1}^{1} \rightarrow \mathrm{He}_{2}^{4}+2 e_{1}^{0}+\mathrm{Q}$

Formula Chart:

Example 1:  A moving proton and electron have the same de-Broglie wavelength. If $K$ and $P$ denote the $K . E$. and momentum respectively. Then choose the correct option :

(A) $K_{p}<K_{e}$ and $P_{p}=P_{e}$

(B) $\mathrm{K}_{\mathrm{p}}=\mathrm{K}_{\mathrm{e}}$ and $\mathrm{P}_{\mathrm{p}}=\mathrm{P}_{\mathrm{e}}$

(c) $K_{p}<K_{e}$ an $\mathrm{P}_{p}<P_{e}$

(D) $\mathrm{K}_{\mathrm{p}}>\mathrm{K}_{\mathrm{e}}$ and $\mathrm{P}_{\mathrm{p}}=\mathrm{P}_{\mathrm{e}}$

Answer: A

Explanation:  $\lambda_{p}=\dfrac{h}{P_{p}}$

$\lambda_{e}=\dfrac{h}{P_{e}}$

$\because \lambda_{p}=\lambda_{e}$

$\Rightarrow P_{p}=P_{e}$

$(K)_{p}=\dfrac{P_{p}^{2}}{2 m_{p}}$

$(K)_{e}=\dfrac{P_{e}^{2}}{2 m_{e}}$

$\mathrm{~K}_{\mathrm{p}}<\mathrm{K}_{\mathrm{e}} \text { as } \mathrm{m}_{\mathrm{p}}>\mathrm{m}_{\mathrm{e}}$Option (a)

Note : A particle or photon's de-Broglie wavelength is given by $\[\mathbf{\lambda }\text{ }=\text{ }\mathbf{h}/\mathbf{p}\]$, where h is Planck's constant and p represents momentum. Because the electron and photon have the same wavelength, their momentum will be the same. When a proton and an electron have the same de Broglie wavelength, their momentum is identical.

Example 2: A radioactive material decays by simultaneous emissions of two particles with half lives of 1400 years and 700 years respectively. What will be the time after which one third of the material remains ? (Take $\ln 3=1.1)$

(A) 740 years

(B) 1110 years

(C) 700 years

(D) 340 years

Answer: A

Explanation: 

Here, radioactive material $X$ is decayed into two particles $Y$ and $Z$ with their respective decay constant, $\lambda_{\mathrm{a}}$ and $\lambda_{\mathrm{b}}$. It means that

$\because \lambda=\frac{\ln 2}{t_{1 / 2}}$

where, $t_{1 / 2}(a)=700 \mathrm{yr}$

and $t_{1 / 2}(b)=1400 \mathrm{yr}$

$\lambda_{a}=\frac{\ln 2}{700} y r^{-1} \text { and } \lambda_{b}=\frac{\ln 2}{1400} y r^{-1}$

$\because \lambda_{\text {total }}=\lambda_{a}+\lambda_{b}$

$=\left(\frac{\ln 2}{700}+\frac{\ln 2}{1400}\right) y r^{-1}=\ln 2\left(\frac{1}{700}+\frac{1}{1400}\right) y r^{-1}$

$=\left(\frac{3 \ln 2}{1400}\right) y r^{-1}$

Suppose the initial number of radioactive nuclei was $\mathrm{N}_{0}$.

$\therefore N=N_{0} e^{-\lambda t}$

where, $\mathrm{N}=$ number of nuclei present at time $=\mathrm{t}$ and $\mathrm{N}_{0}=$ number of nuclei present at time $=0$

$\Rightarrow \frac{N_{0}}{3}=N_{0} e^{-\lambda t} \text { or } \frac{N_{0}}{3}=N_{0} N_{0} e^{-\lambda_{\text {total }} t} \Rightarrow \frac{1}{3}=e^{-\lambda_{\text {total }} t}$

Taking log on both the sides of above equation, we get

$\ln \left(\frac{1}{3}\right)=\ln \left(e^{-\lambda_{\text {total }} t}\right)$

$\Rightarrow \ln \left(\frac{1}{3}\right)=-\lambda_{\text {total }} t$

$\Rightarrow 1.1=\frac{3 \times 0.693}{1400} \times t$

$\Rightarrow \mathrm{t} \approx 740 \mathrm{yr}$

Common Errors or Mistakes That Should be Avoided By the Students Keeping the Exam Point of View:

• Students Forget to write the working formula.

• Students also write improper units without checking their compatibility.

• Calculation errors when doing problems

• Students forget to put in the correct data they used in the working formula, which is used by teachers to check how effective the students' learning is.

• A  law stated by someone cannot be restructured, it should be reiterated like how it was stated.

• While drawing a graph, students forget to state the variables of the graph and just plot the graph.

• For questions which require the reason for a certain condition, firstly students are required to state the cause of the condition and then the consequence of the condition.

Importance of Physics Chapter Modern Physics

As mentioned earlier, Modern Physics deals with scientific principles, theories, hypotheses, concepts, and doctrines developed by contemporary scientists and physicists. These scientific principles date back from the 20th Century to the modern era. This chapter explains how far we have come in this subject by defining the level of thought we have achieved.

The Weightage of Modern Physics in JEE Advanced exam is quite significant for the aspirants. Fundamental questions from this chapter constitute the JEE Advanced exam paper. Students will have to study this chapter to complete their IIT JEE exam preparation.

This chapter is important as it opens a dimension where students will learn the latest inventions and discoveries of modern physics. They will also get a new dimension to scout and find out more about these domains of modern physics and choose their career paths.

Topics like quantum theory, photoelectric effect, photon theory, atomic model, etc. will make the students think about what they have studied and correlate. This chapter is indeed a unique addition to the JEE Advanced syllabus that makes students question what they have studied in the previous years.

Benefits of Vedantu’s Modern Physics IIT JEE Notes

• These notes have been designed to focus on the modern physics topics mentioned above. There are so many new things this chapter will introduce to the students. They will find out how the scientists and physicists have theorised these concepts and established them with facts.

• This intriguing chapter will surely make students think and question their knowledge of Physics. The notes will help them to realise the fact that so many things are yet to be proved or discovered.

• These notes will enable students to understand all the concepts faster and better. They will learn how to study this chapter elaborately and use these notes to revise it. The concise format of this chapter will help students to remember every concept they have studied and frame the right answers in no time.

• Use the sample questions to test your preparation level for this chapter. Gain confidence by using these revision notes and learn how to answer questions from the solutions given.

Download Modern Physics Notes for IIT JEE PDF

Get the free version of these revision notes and prepare this chapter easily. Learn how the experts have simplified the concepts to make your study sessions more productive. Get the best outcomes from your revision sessions by using these notes and score well in the competitive exams.

Important Related Links for JEE Main and JEE Advanced