Question

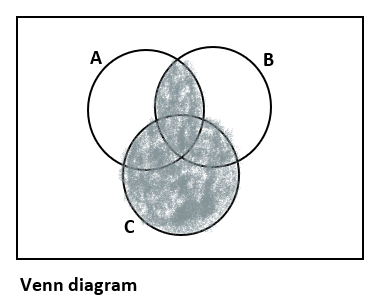
What does the shaded region in the Venn diagram given below represents?


A. \[C\cap ({{A}^{'}}\cap {{B}^{'}})\]
B. \[C\cup ({{C}^{'}}\cap A\cap B)\]
C. \[C\cup (C\cap A)\cup (C\cap B)\]
D. \[C\cup (A/B)\]

Answer 1

Hint: In this question, we are to find the representation of the shaded region in the given Venn diagram. Here we can choose the options by drawing their Venn diagram. This is because a Venn diagram expresses set operations more efficiently. So, we get the required region’s representation by drawing Venn diagrams for each of the given set operations.

Formula Used: Set: A collection of objects in which it is possible to decide whether a given object belongs to the collection or not is said to be a set. Those objects are nothing but the elements in the set.
Sets are represented in two ways: The roaster method and the set builder form
Roaster method:
The set of vowels – \[\left\{ a,\text{ }e,\text{ }i,\text{ }o,\text{ }u \right\}\]
The set of natural numbers – \[\left\{ 1,\text{ }2,\text{ }3,\text{ }\ldots. \right\}\]
Set builder form:
The set of vowels – \[\left\{ x:x\text{ }is\text{ }a\text{ }vowel\text{ }in\text{ }English\text{ }alphabet \right\}\]
The set of natural numbers – \[\left\{ x:x\text{ }is\text{ }a\text{ }natural\text{ }number \right\}\]
Some of the important mathematical sets:
$N$ - the natural number’s set - $N=\{1,2,3...\}$
$Z$- the set of integers - $Z=\{0,\pm 1,\pm 2,\pm 3,...\}$
If two sets $A,B$ where the set $A$ is said to be the subset of $B$ i.e., $A\subseteq B$ then every element of $A$ is in the set $B$ and the set $A$ is said to be the proper subset of $B$ i.e., \[A\subset B\] then $A\subseteq B$ and $A\ne B$.

Complete step by step solution: Given Venn diagram is

 
From the diagram, we can write
\[C\cup (A\cap C)\cup (B\cap C)\cup (A\cap B)\text{ }...(1)\]
Since we know that \[C\cup (A\cap C)=C\cup (B\cap C)=C;\],
then (1) becomes
\[C\cup (A\cap C)\cup (B\cap C)\cup (A\cap B)=C\cup (A\cap B)\]
Where $A\cap B=(A\cap B)-(A\cap B\cap C)$
So,
\[\begin{align}
  & C\cup (A\cap B)=C\cup \left( (A\cap B)-(A\cap B\cap C) \right) \\
 & \text{ }=C\cup \left( A\cap B\cap {{C}^{'}} \right) \\
 & \text{ }=C\cup \left( {{C}^{'}}\cap B\cap A \right) \\
\end{align}\]
Thus, the shaded region in the above Venn diagram represents \[C\cup ({{C}^{'}}\cap A\cap B)\].
Checking for the other options:
We have the first option as \[C\cap ({{A}^{'}}\cap {{B}^{'}})\]
We can write it as \[C\cap ({{A}^{'}}\cap {{B}^{'}})=C\cap {{(A\cup B)}^{c}}\]
Then, its Venn diagram is

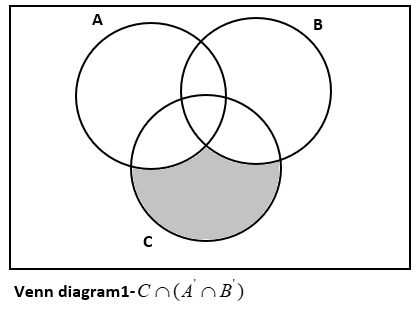
Thus, \[C\cap ({{A}^{'}}\cap {{B}^{'}})\] doesn’t represent the given shaded region.
Similarly, third option we have \[C\cup (C\cap A)\cup (C\cap B)\]
We can write it as
\[\begin{align}
  & C\cup (C\cap A)\cup (C\cap B)=\left( C\cup (C\cap A) \right)\cup (C\cap B) \\
 & \because C\cup (C\cap A)=C \\
 & C\cup (C\cap A)\cup (C\cap B)=C\cup (C\cap B) \\
 & \because C\cup (C\cap B)=C \\
 & C\cup (C\cap A)\cup (C\cap B)=C \\
\end{align}\]
Its Venn diagram is

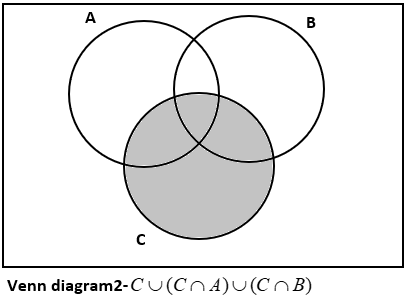
Thus, \[C\cup (C\cap A)\cup (C\cap B)\] doesn’t represent the given shaded region.
And \[C\cup (A/B)\] is not possible.
Thus, the second option is the required representation for the given shaded region.

Option ‘B’ is correct

Note: By drawing Venn diagrams for each option given here is an easy method to extract the required set operation for the given shaded region.