JEE Advanced 2024 Solid State Notes

In crystalline solid, atoms, ions or molecules are arranged orderly in a three-dimensional manner due to strong binding force.

Due to this arrangement, crystalline solids acquire rigidity and definite geometric shape or crystalline structures.

Characteristics Properties of the Solids

• They have definite mass, volume and shape.

• Intermolecular distance is short.

• Intermolecular forces are strong.

• Their constituent particles (atom, molecules or ions) have fixed positions and can only oscillate about their mean position.

• Their existence of a substance in more than one solid modification is called Polymorphism.

Anisotropy: Crystalline solids are anisotropic in nature, that is, some of their physical properties like electrical resistance or refractive index show different values when measured along with different directions in the same crystals. This arises from the different arrangements of particles in different directions.

Isotropy: Amorphous solids on the other hand are isotropic in nature, it is because there is no long-range order in them and arrangement is irregular along with all the directions. Therefore, the value of any physical property would be the same in any direction.

Annealing: An amorphous substance, on heating at a certain temperature, may attain crystalline nature while on cooling regains its amorphous nature, this phenomenon is called annealing.

Difference Between Crystalline and Amorphous Solids: 

Property	Crystalline solids	Amorphous solids
Shape	Definite characteristics, geometrical shape.	Irregular shape.
Melting point	Melt at a sharp and characteristic temperature.	Gradually soften over a range of temperature.
Cleavage property	When cut with a sharp-edged tool, they split into two pieces that are plain and smooth.	When cut with a Sharpe-edged tool, they cut into two pieces with an irregular surface.
Heat of fusion	They have definite and characteristics value.	They do not have definite value.
Anisotropy	Anisotropic in nature except, for cubic crystals.	Isotropic in nature.
Nature	True solids	Pseudo solids or super cooled liquids
Order in arrangement of constituent particles	Long range order	Only short-range order
Law of crystallography	Follows	Does not follow
X-ray diffraction bands	Forms	Does not form
Cooling Curve	Cooling curve is not smooth	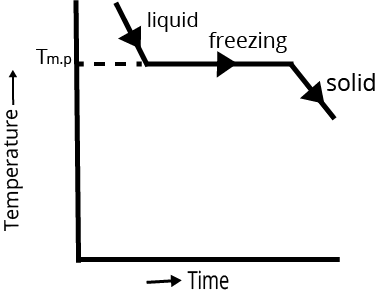Cooling curve is smooth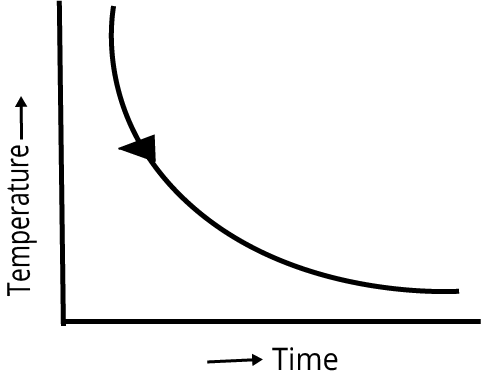
Example	NaCl, Diamond, MgO	Glass, Rubber, Plastic, Quartz glass

Classification of Crystalline Solids:

A crystal is classified as ionic, covalent, metallic and molecular according to the nature of the building units, chemical bonding and the intermolecular forces in the crystal.

Different Types of Solids:

Law of Crystallography:

The study of structure, geometry, and properties of crystals is called Crystallography.

Different Law of Crystallography is

1. Law of Constancy of Interfacial Angle:  measured at the same temperature, a similar angle on crystals of the same substance remains constant regardless of the size and shape of the crystal.

2. Law of Constancy of Symmetry:  The symmetry in all crystals of a particular species is constant though, i.e., the crystals of the same substance possess the same symmetry of element.

The Symmetry of Elements is:

• Plane of symmetry

• Axis of symmetry 

• Centre of symmetry

3. Law of Rational Indices: The law of rational indices states that the intercept of any face of crystal along the crystallographic axes is either equal to the unit intercept or some simple whole number multiples of them.

Unit Cell

The smallest portion of the crystal lattice which can be used as a repetitive unit in a three-dimension manner to get the entire crystal lattice is called a unit cell.

They are broadly divided into two categories, primitive and centred unit cells.

a. Primitive Unit Cell: when constituent particles are present only in the corner position of a unit cell, it is called a primitive unit cell

Primitive Unit Cell

b. Centred Unit Cell: When a unit cell contains one or more constituent particles present at a position other than corners in addition to those at corners, it is called a centred unit cell.

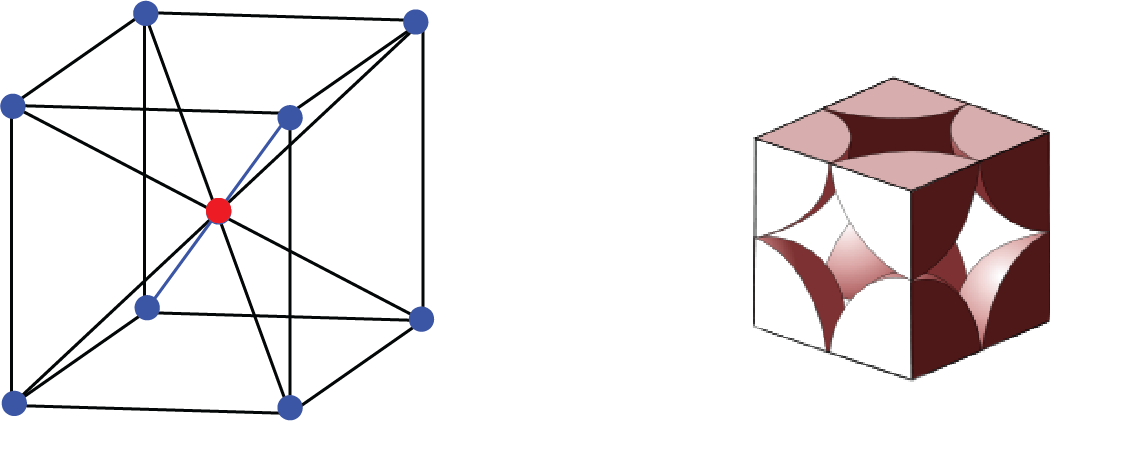
Centred Unit Cell

There are 3 Types:

• Simple cubic cell

• Body-centred unit cell
  
  

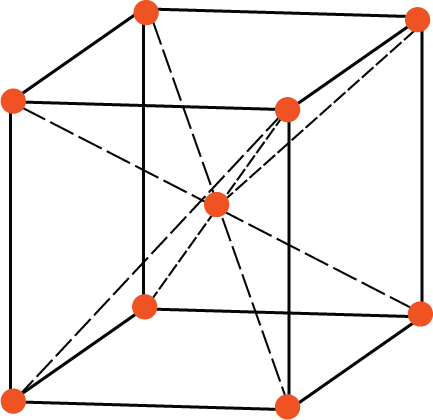
Body-Centred Unit Cell

• Face-centred cell
  
  

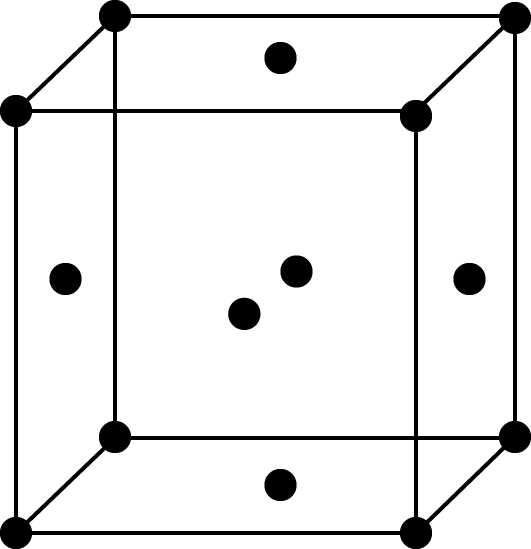
Face-Centred Cell

Bravais Lattices: 

• Bravais Lattices showed there are 14 different possible kinds of three-dimensional lattices.

• These 14 Bravais lattices are grouped into seven crystal systems based on unit cell symmetry.

These Seven Crystal Systems are: 

Seven Crystal Systems:

Seven Crystal System

• The two tetragonal: one side different length to the other, two angles between face all 90°

• The four orthorhombic lattices: unequal sides, angles between faces all 90°

• The two monoclinic lattices: unequal sides, two faces have angle different to 90°

Coordination Number for Elemental Crystallization:

The coordination number is the number of nearest such lattice point surrounding a lattice point in a crystalline.

Simple Cubic Cell: In a lattice of this type, each corner atom is shared by eight-unit cells, four in one layer and four in the layer above it.

Thus, the contribution of each atom placed at the corner of the single cubic unit cell is $\dfrac{1}{8} \times 8 = 1$. Thus, the rank of a primitive unit cell is 1.

BCC Unit Cell: In a BCC lattice, each corner atom is shared by 8-unit cells while the body-centred atom is not shared by any other unit cell. So, the number of effective atoms associated with a BCC unit cell is  $\left[ {\dfrac{1}{8} \times 8} \right] + 1 = 2$. Thus, the rank of the BCC unit cell is 2.

FCC Unit Cell: In an FCC unit cell, each corner atom is shared by 8-unit cells and each face centred atom is shared by 2-unit cells, so the number of effective atoms in an FCC unit cell would be $\left[ {\dfrac{1}{8} \times 8} \right] + \left[ {\dfrac{1}{2} \times 6} \right] = 4$, thus the rank of FCC unit cell is 4.

HCP Unit Cell: Each corner atom would be common to 6 other unit cells, therefore their contribution to one unit cell would be $\dfrac{1}{6}$, Total number of atom in 1 hcp cell $ = \dfrac{{12}}{6}$(from 12 corners)+$\dfrac{2}{2}$(from 2 face centred)+$\dfrac{3}{1}$(from body centre)=6.

Coordination Number and Radius Ratio

Coordination number and radius ratio are important concepts in solid-state chemistry, particularly in the study of crystal structures and bonding. Here's some content explaining these concepts:

Coordination Number:

The coordination number of an atom in a crystal structure refers to the number of nearest neighbour atoms that are directly bonded to it. It indicates how many atoms are in direct contact with a central atom.

• In simple terms, the coordination number is like the number of close friends surrounding a person in a crowd. The more friends surrounding them, the higher the coordination number.

• For example, in a cubic crystal lattice like NaCl (sodium chloride), each sodium ion is surrounded by 6 chloride ions, giving it a coordination number of 6. Similarly, each chloride ion is surrounded by 6 sodium ions.

• Coordination numbers can vary depending on the crystal structure and the type of bonding present. Common coordination numbers include 4, 6, 8, and 12.

Radius Ratio:

The radius ratio is a ratio used to describe the relative sizes of ions or atoms in a crystal structure. It helps predict the coordination number of an ion in a crystal lattice.

• The radius ratio is calculated by dividing the radius of the cation by the radius of the anion (or vice versa), where the cation is the positively charged ion and the anion is the negatively charged ion.

• A radius ratio less than 0.155 generally predicts a coordination number of 2.

• A radius ratio between 0.155 and 0.225 generally predicts a coordination number of 4.

• A radius ratio between 0.225 and 0.414 generally predicts a coordination number of 6.

• A radius ratio between 0.414 and 0.732 generally predicts a coordination number of 8.

• A radius ratio greater than 0.732 generally predicts a coordination number of 12.

Importance of Coordination Number and Radius Ratio:

• These concepts help in understanding and predicting the crystal structures of various compounds.

• By knowing the coordination number and radius ratio, we can predict the geometry of crystal lattices and understand the arrangement of atoms or ions in solids.

• They are crucial for understanding properties like mechanical strength, electrical conductivity, and optical behaviour of materials.

Example:

Consider the crystal structure of cesium chloride (CsCl). Cesium has a coordination number of 8, and chloride has a coordination number of 8 as well. The radius ratio of CsCl is 0.414, which corresponds to a coordination number of 8 according to the radius ratio rule.

Hexagonal Closest Packing of Spheres:

• Normal 

• Diagrammatic view

Interstitial Voids: The empty spaces between the three-dimensional layers are known as holes or voids. The holes are also referred to as interstices. There are three types of holes possible.

Tetrahedral Holes:  A hole formed by three spheres in contact with each other of a layer. The holes are also referred to as interstices.

Radius ratio of the tetrahedral void,$\dfrac{{{r_{void}}}}{{{r_{sphere}}}} = 0.225$

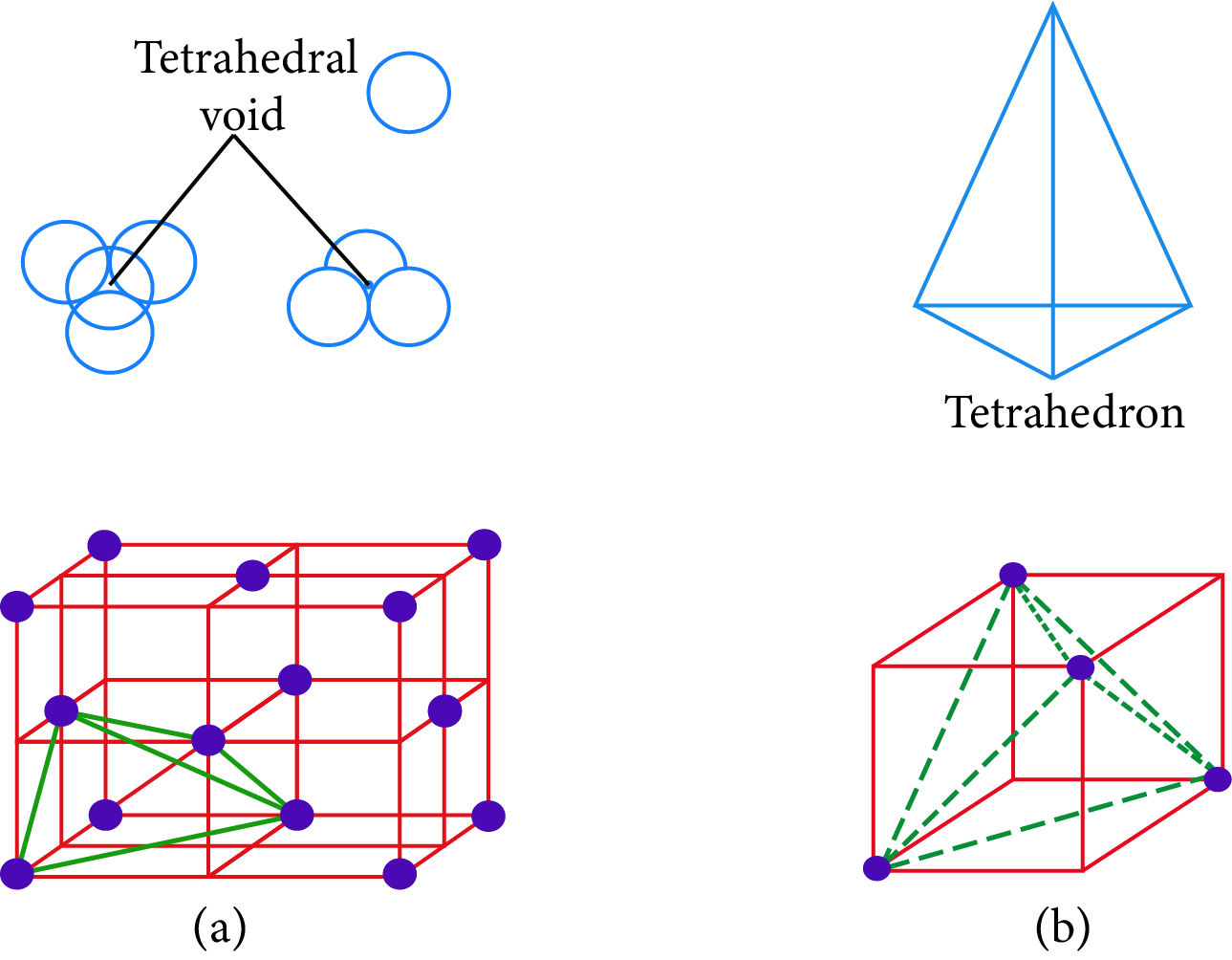
Tetrahedral Hole 

Octahedral Hole: It is the vacant space between a group of three-sphere in a layer and another set of three-sphere in the next layer, these six spheres surrounding the hole, lie at the vertices of a regular octahedral.

The total number of octahedral voids $= 1 + 12 \times \dfrac{1}{4} = 1 + 3 = 4$

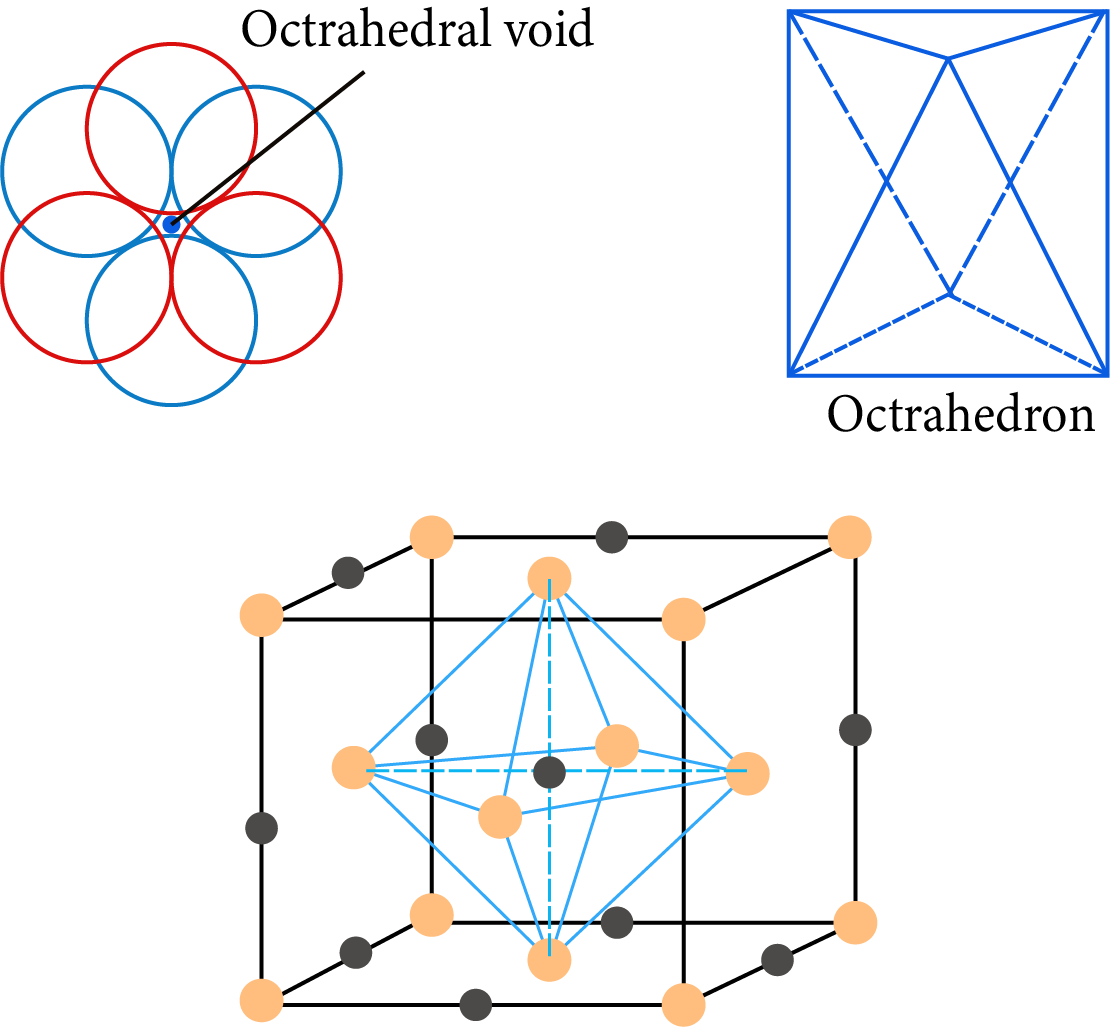
Octahedral Hole

Types of Ionic Structures

The term "ionic structure" refers to the arrangement of positively (Cations) and negatively (Anions) charged ions in a compound. Ionic compounds are formed when atoms of different elements transfer electrons to each other, resulting in the formation of ions. These ions are held together by strong electrostatic forces, forming a three-dimensional lattice structure.

1. Rock Salt Structure (NaCl):

• In the rock salt structure, chloride ions (Cl⁻) occupy both the corners and the face centres of a face-centered cubic (FCC) lattice, while sodium ions (Na⁺) occupy the octahedral voids within the lattice.

• Both sodium and chloride ions have a coordination number of 6.

2. Zinc Blende (Sphalerite) Structure (ZnS):

• In the zinc blende structure, sulfide ions (S²⁻) occupy the main lattice sites, while zinc ions (Zn²⁺) are located in the alternate tetrahedral voids of the FCC crystal lattice.

• The coordination number of sulfide and zinc ions is 4.

3. Fluorite Structure (CaF₂):

• In the fluorite structure, calcium ions (Ca²⁺) occupy the main lattice positions, and fluoride ions (F⁻) occupy the tetrahedral voids within the FCC crystal structure.

• The coordination number of calcium ions is 8, while that of fluoride ions is 4.

4. Anti-Fluorite Structure:

• Commonly found in alkali oxides like Na₂O and Li₂O, the anti-fluorite structure consists of oxide ions (O²⁻) occupying the FCC lattice positions, while lithium ions (Li⁺) are located in the tetrahedral voids.

• The coordination number of lithium ions is 4, and that of oxide ions is 8.

5. Cesium Halide Structure (CsCl):

• In the cesium halide structure, chloride ions (Cl⁻) are positioned at the corners of the unit cell, while cesium ions (Cs⁺) are located at the center of the cell.

• Both chloride and cesium ions have a coordination number of 8.

6. Corundum Structure (Al₂O₃):

• In the corundum structure, oxygen ions (O²⁻) form a hexagonal close-packed (hcp) lattice, while aluminum ions (Al³⁺) occupy 2/3 of the octahedral voids within the lattice.

7. Rutile Structure (TiO₂):

• In the rutile structure, oxygen ions (O²⁻) form a hcp lattice, and titanium ions (Ti⁴⁺) occupy half of the octahedral voids within the lattice.

8. Perovskite Structure (CaTiO₃):

• In the perovskite structure, calcium ions (Ca²⁺) are located at the corners of the unit cell, oxygen ions (O²⁻) are positioned at the face centers, and titanium ions (Ti⁴⁺) are situated at the centre of the unit cell.

Packing Fraction in Element Crystallization:

• Percentage efficient of simple cubic unit cell =$\dfrac{{{\text{volume of one sphere}}}}{{{\text{volume of unit cell}}}}{\text{ }\times 100}$

${a^3}$= volume of the unit cell 

$a = 2{r_s}$ where ${r_s}$ is the radius of the sphere.

$\dfrac{{\dfrac{4}{3}\pi  \times {{({r_s})}^3}}}{{{a^3}}} \times 100 = \dfrac{{\dfrac{4}{3}\pi  \times {{({r_s})}^3}}}{{{{\left( {2 \times {r_3}} \right)}^3}}} \times 100$

$= \dfrac{{\dfrac{4}{3}\pi }}{8} \times 100 = 52.3$ 

• Percentage efficiency of body-centred unit cell =$\dfrac{{{\text{volume of the two sphere}}}}{{{\text{Volume of cube}}}}{\text{ }\times 100}$

${a^3}$= volume of the unit cell by taking edge length ‘a’

$a = 2{r_s}$where ${r_s}$ is the radius of the sphere.

\[\dfrac{{2 \times \dfrac{4}{3}\pi {{({r_s})}^3}}}{{{a^3}}} \times 100 = \dfrac{{2 \times \dfrac{4}{3}\pi {{({r_s})}^3}}}{{{{\left( {\dfrac{4}{{\sqrt 3 }}{r_s}} \right)}^3}}} \times 100 = 68.05\]

The volume occupied by spheres in a body-centred unit cell is 68.05% and void volume is 31.95%

Length of facial diagonal -$\sqrt{2a}$

Length of body diagonal -$\sqrt{3}a$

• Efficiency of packing in face-centred unit cell = $\dfrac{{{\text{volume of the four sphere}}}}{{{\text{Volume of cube}}}}{\text{ }\times 100}$

${a^3}$= volume of the unit cell by taking edge length ‘a’

$a = 2{r_s}$where ${r_s}$ is the radius of the sphere.

\[\dfrac{{4 \times \dfrac{4}{3}\pi {{({r_s})}^3}}}{{{a^3}}} \times 100 = \dfrac{{4 \times \dfrac{4}{3}\pi {{({r_s})}^3}}}{{{{\left( {2\sqrt 2 {r_s}} \right)}^3}}} \times 100 = 74.06\]

Thus, the volume occupied by a sphere in face-centred unit cell (cpp arrangement) is 74.06% and the void volume is 25.94%

• Volume Fraction in HCP: 

$V.F = \dfrac{{6 \times \dfrac{4}{3}\pi {R^3}}}{{{V_{HCP}}}}$

${{\text{V}}_{{\text{HCP}}}}{\text{ = Area of base  }\times  Height}$

${\text{ = 3}}\sqrt {2{a^3}}  = 24\sqrt 2 {R^3}$ 

Volume fraction of HCP=$4\sqrt {\dfrac{2}{3}} R$

Note: Distance between A and B layer in CCP or HCP=$2\sqrt {\dfrac{2}{3}} R$

Bragg’s Equation: $n\lambda  = 2d\sin \theta $

n= order of reflection

$\lambda$=wave length of incident x-ray

d= interplanar distance

$\theta$=angle of reflection

Types of Crystal Defects:

• Intrinsic Defect: These are seen in pure crystal.

• Extrinsic Defects: These are due to the impurities in the solids.

• Point Defect: These Occur at the lattice points or sites in the crystals.

• Extended Crystal: These are present in one or more dimensions.

Stoichiometric Defects:

Ionic Solids Show Two Types of Defects 

1. Schottky Defect

• This defect arises due to vacancy at cation sites and equal number of vacancies at anion sites

• Condition for the defect:

High co-ordination numbers and where the positive and negative ions are of similar size, i.e., $\dfrac{{{r^ + }}}{{{r^ - }}} \cong 1$

• Number of Schottky defect

• $n = N{e^{ - E/2kt}}$

• $n = {\left( {N{N_i}} \right)^{1/2}}{e^{ - E/2kt}}$

K = Boltzmann’s constant

T= Kelvin temperature

E= energy required to create defect 

N= number of ions present 

Ni= number of interstitial spaces

2. Frenkel Defect

• This type of defect arises due to a vacancy at a cation site.

• Conditions that favour the defect:

Large difference in size between cation and anion and Compounds having ions of different size i.e., $\dfrac{{{r^ + }}}{{{r^ - }}}$ is low since positive ions are smaller than negative ions.

Doping: 

• Addition of B(IIIA Group) or P or As (VA Group) element to alter the conductivity of Ge(or) Si is called Doping.

• Pure Si (or) Ge are an intrinsic semiconductor. 

• In doping, group IIIA(13 group element) elements behave as electrons acceptor and group VA(15 group elements) elements behave as donor.

Importance of Physical Chemistry Solid State

Here you will learn the different aspects of the Solid State at an advanced level. This chapter will explain how the molecules form solid and what their characteristics are.

Go through these notes to quickly revise the physical properties of a solid and realize how this state of matter is defined. With the knowledge of the physical properties of different solids, differentiate, distinguish, and identify different materials. This chapter will also describe the classification of solids following the various features.

The importance of this chapter is that it explains the different physical properties of all classes of solids with examples. All these classifications are done based on particular parameters such as crystal structure and chemical bonding. It will also explain how lattices are formed and what kinds of lattices exist with pictorial illustrations. Get Solid State for JEE Advanced key concepts from the chapter and refer to these notes for a quick revision.

Benefits of Vedantu’s Solid State JEE Notes PDF

• The revision notes offer a simpler explanation of all the advanced concepts of this chapter in an easy-to-understand language. You will find it easier to learn different types of solids, types of crystalline structures, their examples, and all other topics included in this chapter.

• The simpler version of this chapter in the Solid State JEE notes PDF will help you complete preparing this chapter in no time. You will find learning the fundamental principles much easier. In fact, you can also resolve doubts on your own and proceed to solve exercise questions without any difficulty.

• These revision notes are the easiest way to revise the chapter before the exam date. These notes also come with Solid State JEE Advanced questions and answers prepared by the experts. Students can try to solve the questions on their own and check their preparation level.

• Students can easily recall all the concepts, definitions, derivations, formulas, etc of this chapter by using these notes to score well in the competitive exam.

Download Solid State JEE Revision Notes PDF

Students can add the free PDF version of these revision notes and questions to their JEE Advanced preparation material for this chapter. Many students prefer to use these notes to make their study sessions more productive. The simpler format of these notes will help them to recall the definitions, explanations, formulas, and derivations of this chapter without any difficulty.

Important Related Links for JEE Main and JEE Advanced