JEE Advanced 2023 Revision Notes for Chemistry Energetics

Chemical Thermodynamics deals with the quantitative relation between heat energy and other forms of energy in physicochemical processes.

Chemical Thermodynamics

• Chemical thermodynamics is said to be the branch of thermodynamics that deals with the study of the process in which chemical energy is involved. 

• Thermodynamics predicts the energy metamorphoses and feasibility of a process.

Phase: It is a homogeneous portion which has identical physical and chemical properties throughout it and is physically distinct and mechanical separable from another portion.

In a solid mixture, the number of individual solids is equal to the number of phases.

Ex: ${{\text{C}}_{{\text{(graphite)}}}} \rightleftharpoons {{\text{C}}_{{\text{(diamond)}}}}$, number of phases is equal to two.

Terms Used in Thermodynamics:

If any part of the system that's under thermodynamic study. The remaining part of the system is called girding or surrounding.

Universe = System + Surrounding

• Boundary is any real (or) imaginary, rigid (or) non-rigid surface that separates systems and surroundings.

• Diathermic wall which allows heat exchange between system and surroundings.

• Adiabatic wall which does not allow heat exchange between system and surroundings.
  
  

Types of the System: 

1. Open System: The system where matter and energy are exchanged between the system and surroundings.

2. Closed System: The system where only the energy but not the matter is exchanged with the surroundings.

3. Isolated System: Neither matter nor energy is exchanged between the system and surroundings, the boundary is sealed and the insulated.

Universe is treated as an isolated system.

• Homogeneous System is a system conforming to two or further phases.

E.g.: Pure solid, a liquid or a mixture of gases.

• Heterogeneous System: A system conforming to two or further phases 

Ex: water at a triple point consists of three phases.

Thermodynamic Process:

The operation which brings about the change in the state of the system is termed the thermodynamic process.

Isothermal Process: 

Throughout studies, the temperature does not change in a process.

Adiabatic Process: 

An operation in which the commutation of heat between system and surroundings doesn't take place.

For an adiabatic process Q=0

Isobaric Process:

A process in which stress of the system remains changeless throughout the studies ($\Delta P = 0$)

Isochoric Process:

A process in which stress of the complex remains changeless throughout the studies ($\Delta V = 0$)

Cyclic Process:

A process in which the original state of the system is recaptured after a series of operation.

$\Delta $(state function)=0, $\Delta $(path function)≠0

Thermodynamic Equilibrium:

When a system exits simultaneously in a thermal equilibrium, mechanical equilibrium and chemical equilibrium is said to be in thermodynamic equilibrium.

Reversible Process:

A reversible process (or quasistatic process) is one in which all changes occurring at any part of the process are exactly reversed when change is carried out in the opposite direction. It gives rise to maximum work in the expansion.

Gas in cylinder system displaying the reversible expansion ${P_{gas}} = {P_{external}} + dp$

In reversible compression of gas in cylinder system, ${P_{gas}} = {P_{external}} - dp$, dp= infinitesimal change pressure. 

Irreversible Process:

An irreversible process is one in which the direction of the change cannot be reversed by small change in variable, it is real one and all process which naturally occur are irreversible.

• A fast change during investigation.

• Driving force is much advanced than opposing force

$|{W_{rev}}| > |{W_{irrev}}|$, Expansion

$|{W_{rev}}| > |{W_{irrev}}|$, Compression

${W_{isobaric}} > {W_{isothermal}} > {W_{Adiabatic}} > {W_{iIsochoric}}$

• Extensive Property: It depends on the quantity or size of matter present in the system, it is additive property.

• Intensive Property: It does not depend on the quantity or size of matter present in the system, it is non-additive property.

Laws of Thermodynamics:

1. Zeroth law of Thermodynamics:

When two systems is in thermal equilibrium with another system simultaneously then those two systems are also existing in thermal equilibrium.

2. First Law of Thermodynamics:

• It is also known as law of conservation of energy.

• The net energy change in closed system is equal to heat absorbed plus the work done on the system (or) by the system.

      $\Delta $U=Q + W

Enthalpy (H):

The total heat content of a system at constant pressure and temperature is called enthalpy, H=E + PV.

$\Delta $H of gas in cylinder system can be calculated as:

$\Delta H \ne \Delta U + \Delta (PV)$

$\Delta H = \Delta E + nR\Delta T$

$\Delta H = \Delta E + {P_2}{V_2} - {P_1}{V_1}$ 

In exothermic reaction: $\Delta $H = HP – HR = -ve

In endothermic reaction: $\Delta $H = HP – HR = +v

Relation between $\Delta $H  and $\Delta $U

For any chemical change reaction, at any constant temperature, 

$\Delta$r H = $\Delta $r U+$\Delta $ngRT

$\Delta {n_g} = {n_2} - {n_1} = \sum {{{({n_g})}_{products}} - \sum {{{({n_g})}_{reac\tan ts}}} }$

Heat Capacity and Specific Heat:

• Heat capacity (C) of a substance is the amount of heat required to raise its temperature by one degree.

• Heat capacity is the ratio of heat absorbed by a system to the resulting increase in temperature $C=\dfrac{Q}{T}$.

• Heat capacity at constant volume $\left(C_{v}\right)$ gives the measures of the change of internal energy (U) of a system with temperature.

${C_v} = {\left[ {\dfrac{{\partial U}}{{\partial T}}} \right]_v} = \dfrac{{{Q_v}}}{{\Delta T}};\Delta U = n{C_v}\Delta T$

• Heat capacity at constant pressure

• ${C_p} = \dfrac{{\partial H}}{{\partial T}} = \dfrac{{{Q_P}}}{{\Delta T}};\Delta H = n{C_p}\Delta T$

Specific Heat Capacity (Cs or S):

• The amount of heat required to raise the temperature of 1 gram of substance through 1k (or 10C)

• Specific heat capacity (Cs) = $\dfrac{Q}{m}$

${C_s} = \dfrac{Q}{{m\Delta t}}(or)Q = {C_s} \times m \times \Delta T$

Values for ${C_p},{C_v},\gamma $

Free Expansion:

Expansion of gas in vacuum during free expansion of an ideal gas whether the process is reversible (or) irreversible no work is done.

Calculation for Isothermal Process:

$\Delta T = 0,PV = nRT = {P_1}{V_1} = {P_2}{V_2},\Delta E = 0$

Isothermal Process in Finite Number of Steps:

Joule-Thomson Effect:

It is the phenomenon of observation of cooling effect when gas is adiabatically expanded from higher to lower pressure region through pours plug.

Conditions:

$\Delta$ H=0

Q=0

Joule-Thomson coefficient ${\mu _{JT}} = \dfrac{{dT}}{{dP}}$

• Exothermic Reaction: During a chemical reaction if evolution of heat occurs then this is known as exothermic reaction.

• Endothermic Reaction: A chemical reaction, which occurs with the absorption of heat from the surrounding.

Heat reaction: It is amount of heat absorbed or evolved when the reactants are converted into products according to stoic metric equation at constant temperature.

Two types of heat reaction:

Q = QP = $\Delta $H = $\Delta $rH (at constant pressure, temperature)

Q = Qv = $\Delta $E$\Delta $rE (at constant volume, temperature)

Thermochemical Equation:

The chemical equation in which heat change accompanying a reaction is also numerically specified with proper sign $\Delta $H

By the side of the equation is known as thermochemical equation.

Hess’s Law:

The heat energy released or absorbed in a process is same whether the process occurs in one step per several steps.

According to Hess law: ${\Delta _r} = {\Delta _r}{H_1} + {\Delta _r}{H_2} + {\Delta _r}{H_3}$

Heat Engine: It is a device which performs work done by the absorption of heat.

Efficiency of heat engine:

It is a fraction of absorbed heat which converted into work done

$\eta=\dfrac{\text { work done }}{\text { absorbed heat }}=\dfrac{w}{+Q_{2}}=\dfrac{Q_{2}-Q_{1}}{+Q_{2}}$

Carnot’s Heat Engine 

It is operating in reversible cyclic manner and produces maximum work done, hence max efficiency.

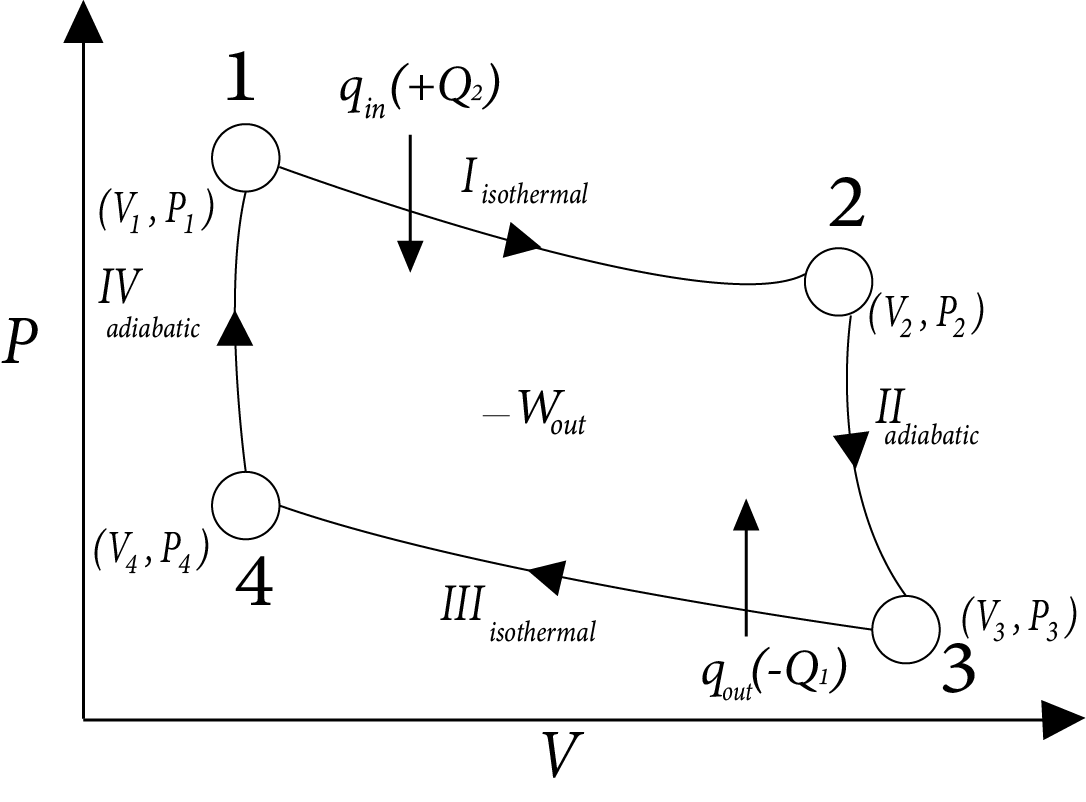
Image: Carnot’s Heat Engine 

$\eta  = \dfrac{{|{W_{net}}|}}{{ + {Q_2}}} = \dfrac{{2.303nR({T_2} - {T_1})\log \left( {\dfrac{{{V_2}}}{{{V_1}}}} \right)}}{{2.303nR{T_2}\log \left[ {\dfrac{{{V_2}}}{{{V_1}}}} \right]}}$

$= \dfrac{{{T_2} - {T_1}}}{{{T_2}}} = 1 - \dfrac{{{T_1}}}{{{T_2}}}$

$\therefore \eta  < 100\%$ 

Entropy

• Measure of randomness or disorder Ness of the molecule of the system.

• Its is state function and extensive property.

$\Delta S = \Delta {S_{final}} - \Delta {S_{inital}}$

${\Delta _r}S = \Delta {S_{products}} - \Delta {S_{reac\tan ts}}$

$\Delta {S_{Total}} = \Delta {S_{system}} + \Delta {S_{surrounding}}$

Entropy Factor:

1. At a given temperature ${S_{gas}} > {S_{liquid}} > {S_{soild}}$

2. $\Delta S\alpha \Delta V$

3. $\Delta S\alpha \Delta {n_g}$

4. $\Delta S\alpha \Delta T$

5. $\Delta S\alpha \dfrac{1}{{\Delta P}}$, at given temperature.

6. $\Delta S\alpha \Delta P$at constant volume.

Spontaneous Process:

It is the process which takes places on its accord (or) after proper imitation under the given set of condition.

Non- Spontaneous Process:

It is the process which doesn’t take place on its own accord (or) after proper imitation.

Effect of temperature on spontaneity of Reaction

Third Law of Thermodynamics:

The entropy of pure and perfectly crystalline substance is zero at the absolute zero temperature (-273℃).

Absolute entropy of a substance at a temperature T, ${S_r} = \int\limits_0^T {\dfrac{{{C_p}}}{T}dT} $

Standard molar entropy: It is entropy of one mole of the substance at 25°C 1atm pressure.

Calculating of Entropy:

1. $\Delta S = \dfrac{{{Q_{rev}}}}{T}$

2. $\Delta {S_{sys}} = 2.303n{C_v}\log \left( {\dfrac{{{T_2}}}{{{T_1}}}} \right) + 2.303nR\log \left( {\dfrac{{{V_2}}}{{{V_1}}}} \right)$

3. $\Delta {S_{sys}} = 2.303n{C_v}\log \left( {\dfrac{{{T_2}}}{{{T_1}}}} \right) + 2.303nR\log \left( {\dfrac{{{p_2}}}{{{p_1}}}} \right)$

Trouton’s law: The molar entropy of vaporization of most of liquids which doesn’t involve hydrogen bonding and also don’t possess boiling less than 150K is about 10.5R

$\Delta {S_{vap}} = \dfrac{{\Delta {H_{vap}}}}{{{T_{b.p}}}}$

Gibb;s-HelemHoltz Equation:

1. \[G = \Delta H - T\Delta S\]

2. $G = \Delta H - T\Delta S$ were, 

$- \Delta S = {\left( {\dfrac{{\partial (\Delta G)}}{{\partial T}}} \right)_P}$

$\Delta G = \Delta H + T\left( {\dfrac{{\partial (\Delta G)}}{{\partial T}}} \right)$

3. $- \dfrac{{\Delta H}}{{{T^2}}} = {\left( {\dfrac{{\partial \left( {\dfrac{{\Delta G}}{T}} \right)}}{{\partial T}}} \right)_p}$

Gibb’s Energy Graphs:

Case (I): If

$\Delta G^\circ  = 0 \Rightarrow {K_{eq}} = 1$

$\Delta G^\circ  = 0 \Rightarrow \Delta G_r^\circ  = \Delta G_p^\circ $

i.e ${\left[ {prod} \right]_{eq}} = {\left[ {react} \right]_{eq}}$

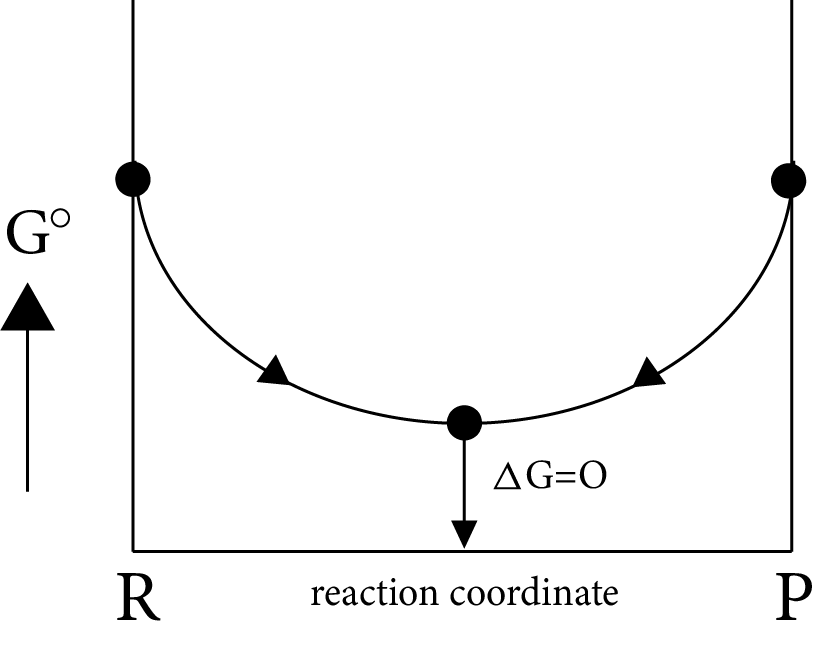
Image: Gibb’s Energy

Minimum energy position in the graph represent equilibrium position delt G=0 i.e., equilibrium position is exactly between reactant and products, i.e., both forward and backward reaction takes same in the same extent.

Case (II): If

$\Delta G^\circ  = more + ve \Rightarrow \Delta G_p^\circ  - \Delta G_R^\circ  =  + ve$

$\Delta G^\circ  = more + ve \Rightarrow \Delta G_p^\circ  >  > \Delta G_R^\circ i.e,{K_{eq}} <  < 1$

i.e ${\left[ {prod} \right]_{eq}} < {\left[ {react} \right]_{eq}}$

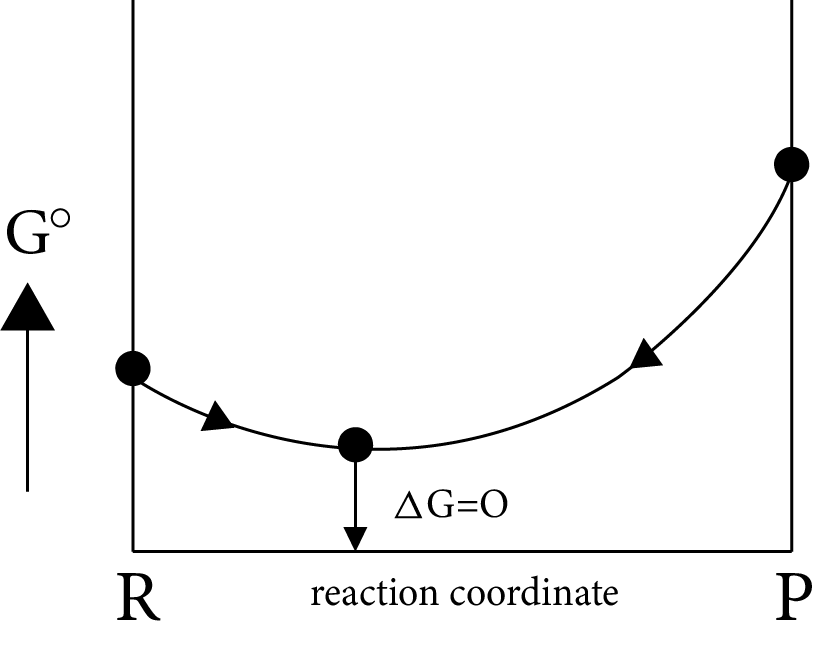
Image: Equilibrium Position

Equilibrium position is nearer to the reactants side, which represents the completion of almost backward reaction.

Case (III)

If

$\Delta G^\circ  = more + ve \Rightarrow \Delta G_p^\circ  - \Delta G_R^\circ  =  - ve$

$\Delta G_p^\circ  <  < \Delta G_R^\circ i.e,{K_{eq}} = {K_p} >  > 1$

i.e ${\left[ {prod} \right]_{eq}} > {\left[ {react} \right]_{eq}}$

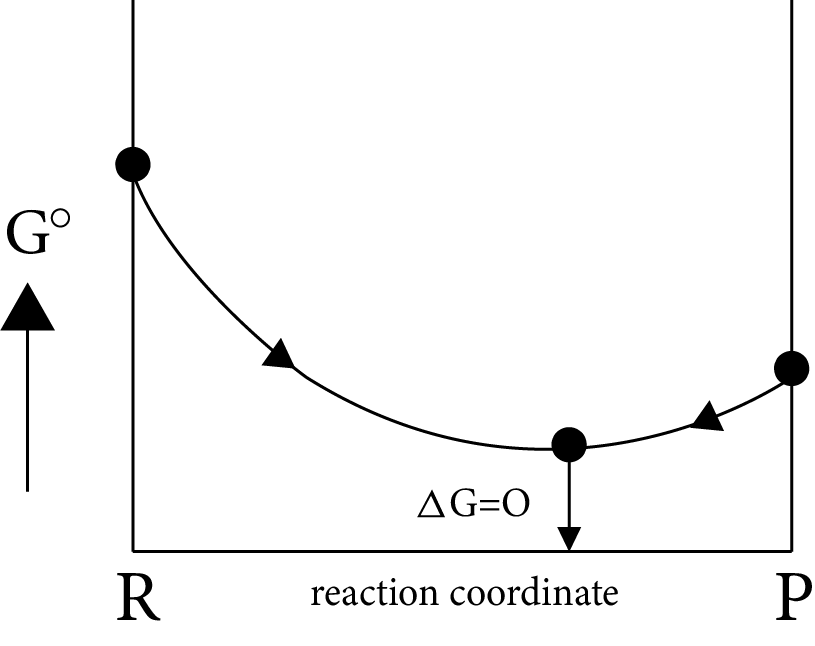
Image:  Equilibrium Position (ii)

(OR)

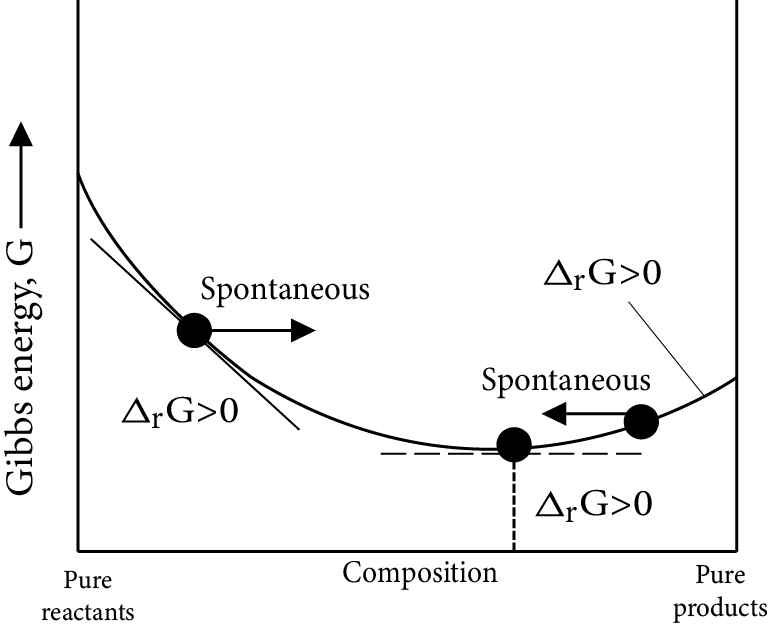
Image: Equilibrium Position (iii)

Equilibrium position is nearer to the product side, which represents the completion of almost forward reaction

Van’t Hoff isochore Equation

Gibb’s Helm-Holtz Equation: $\dfrac{{ - \Delta H^\circ }}{{{T^2}}} = {\left( {\dfrac{{\partial \left( {\dfrac{{\Delta G^\circ }}{T}} \right)}}{{\partial T}}} \right)_P}$

Were, $\Delta G^\circ  =  - RT\log {K_{eq}}$

$\dfrac{{\Delta H^\circ }}{{R{T^2}}} = {\left( {\dfrac{{\partial \ln {K_{eq}}}}{{\partial T}}} \right)_P}$

Where, $\Delta H^\circ $ is standard enthalpy change

i.e., $\dfrac{{\partial \ln {K_p}}}{{\partial T}} = \dfrac{{{\Delta _r}H^\circ }}{{R{T^2}}}$

which shows variation of Keq with temperature.

Nernst’s Equation for Galvanic Cell

Galvanic cell it is the device which converts chemical energy into electric energy by a spontaneous redox chemical reaction.

$\Delta G = \Delta G^\circ  + 2.303RT\log Q$

${E_{cell}} = E_{cell}^\circ  + \dfrac{{2.303RT}}{{nF}}\log Q$

Importance of Physical Chemistry Energetics

Energetics is a significant part of JEE syllabus that teaches students how energy is transformed into different forms. It also teaches how energy flows at all levels or scales. This chapter creates an excellent foundation of knowledge where students can realize how energy flows in the biosphere, in various forms.

This chapter explains the various forms of energies flowing in different systems. It shows how to determine and measure the change in energy flow and its storage under various circumstances.

JEE Advanced Physical Chemistry Energetics covers the advanced concepts and scientific principles related to internal energy, enthalpy, laws of thermodynamics, the heat of reaction, the heat of fusion, vaporization, Hess’s law, and criteria for spontaneity, free energy, and some other concepts. It will also explain the basic concepts of thermo-chemistry.

Throughout the entire syllabus of physical chemistry and in most chemical reactions, you will find relevance and reference to the concepts covered in this chapter. Hence, this chapter is very important to understand the energy movement and transformation at different levels of chemical reactions. The JEE Advanced Physical Chemistry Energetics revision notes available on Vedantu cover all the topics and sub-topics making it easier for students to revise the chapter quickly before the exam.

Benefits of Vedantu’s Energetics JEE Advanced Notes PDF

• These revision notes have been compiled by the subject matter experts. These notes will be ideal for your exam preparation and revision as all the laws, expressions, explanations of concepts, etc., have been simplified for a better understanding. It will help you prepare this chapter fast.

• Referring to the Energetics notes for IIT JEE will help you to resolve your doubts from this chapter on your own. Thermodynamics is a fundamental concept that will be useful for studying advanced concepts of Chemistry. You can expect quite a few questions from this chapter in the JEE Advanced exam. Hence, developing a strong conceptual foundation for the concepts covered in this chapter is required.

• The revision notes can be downloaded for free anytime and anywhere at your convenience. Prepare the concepts of enthalpies, lattice energy, laws, heat engine efficiency, etc., effectively from these revision notes.
  
  

Download Energetics JEE Advanced Revision Notes PDF

Get the free PDF version of Energetics revision notes for JEE Advanced today to prepare for JEE Advanced. Make your study sessions more productive by using these notes. You can revise and practice all the topics covered in this chapter without any difficulty. So download and refer to the Energetics JEE Advanced notes PDF and practice the worksheets to enhance your JEE Advanced preparation.

Important Related Links for JEE Main and JEE Advanced