JEE Chapter - Vectors

A vector is a two-dimensional element containing magnitude and direction both. A vector can be visualized geometrically as a directed line segment with an arrow indicating the vector's direction and a length equal to the vector's magnitude, from the tail to the head of the vector indicating the direction.

In the chapter Vector, we will learn about the basics of the vector-like types, definition, And solved examples along with some previous year's questions for better understanding.

Important Topics of Vectors 

• Addition of Vectors

• Multiplication of Vector with Scalar

• Types of Vector

• Scalar Triple Product

Important Concepts of Vectors

What is a vector?

Vectors are geometric representations of magnitude and direction, generally depicted as straight lines that start at one point on a coordinate axis and finish at another. Every vector has a length, known as the magnitude, that indicates some quality of interest so that it can be compared to another vector. Because vectors are arrows, they have a direction. This distinguishes them from scalars, which are just numbers with no meaning.

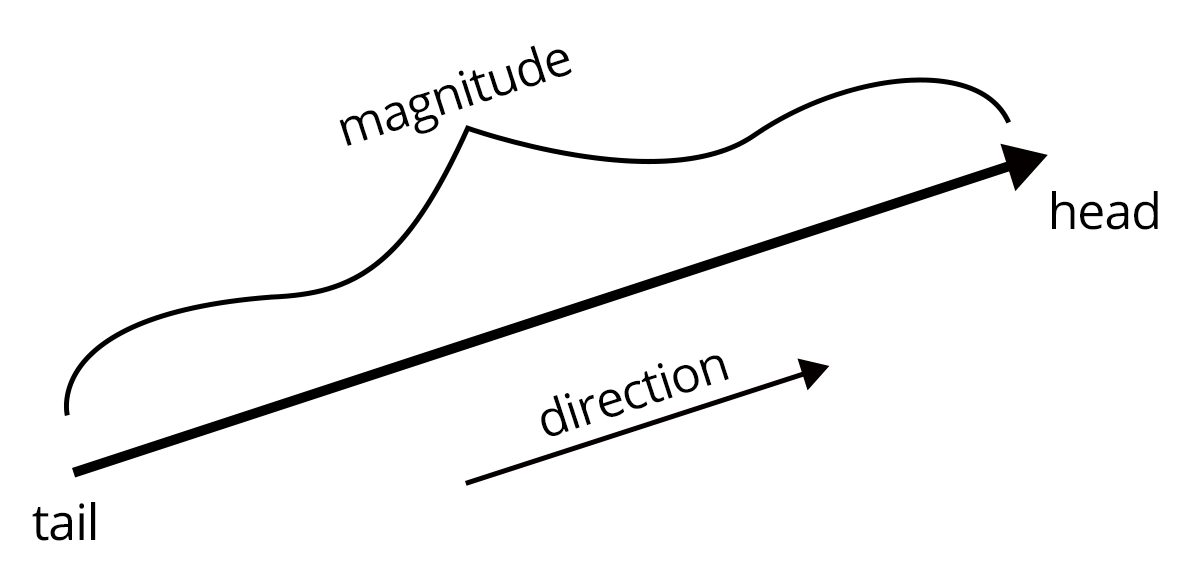
The magnitude and orientation of a vector with respect to a set of coordinates define it. Breaking down vectors into their component pieces is frequently beneficial when examining vectors. These components are horizontal and vertical for two-dimensional vectors. For three dimensional vectors, the magnitude component is the same, but the direction component is expressed in terms of $\text{x}$, $\text{y}$ and $\text{z}$.

Vectors in Euclidean Geometry- Definition

In mathematics, a vector is a geometric entity with both magnitude and direction. Vectors have a starting point at which they begin and a terminal point that indicates the point's final position. Addition, subtraction, and multiplication are some of the operations that can be performed on vectors. 

Vectors - Examples

In physics, vectors are extremely significant. Velocity, displacement, acceleration, and force, for example, are all vector quantities with both a magnitude and a direction.

The Magnitude of Vectors

The square root of the sum of the squares of a vector's components can be used to calculate its magnitude. If $\left ( x,y,z \right )$ are the components of a vector $\text{A}$, then the magnitude formula of A is given by, $\left | A \right |=\sqrt{x^2+y^2+z^2}$

A vector's magnitude is a scalar value.

Angle Between Two Vectors

The dot product formula can be used to calculate the angle between two vectors. Let us consider two vectors a and b and the angle between them to be $\theta$. Then, the dot product of two vectors can be given by a·b = |a||b| cosθ, we need to determine the value of the angle $\theta$. The direction of the two vectors is also shown by the angle between the two vectors. $\theta$ can be evaluated using the following formula:

θ = cos-1[(a·b)/|a||b|]

Scalar Multiplication of Vectors

A scalar is a non-directional real number. When a scalar is multiplied by a vector, each component of the vector is multiplied by the scalar. Scalar multiplication is the process of multiplying a vector by a scalar. When a vector a = ($a_1, a_2, a_3$) = $a_1  \hat i$ + $a_2  \hat j$ + $a_3 \hat k$ is multiplied by a scalar r, the resultant vector is:

ra = ($ra_1, ra_2, ra_3$) = ($ra_1$)e1 + ($ra_2$)e2 + ($ra_3$)e3

If r is negative, the resultant vector's direction changes by 180 degrees.

Scalar multiplication is distributive over vector addition, that is, r(a+b) = ra + rb

Scaling is defined as the multiplication of vectors by any scalar quantity. In vectors, scaling only affects the magnitude and not the direction. Some properties of scalar multiplication in vectors are given below:

k(a + b) = ka + kb

(k + l)a = ka + la

a·1 = a

a·0 = 0

a·(-1) = -a

Scalar Triple Product of Vectors

It's one vector's dot multiplied by the cross product of the other two vectors. In a scalar triple product, if any two vectors are equal, the scalar triple product is zero. The three vectors a, b, and c are said to be coplanar if the scalar triple product is equal to zero. Also, a·(b × c) = b·(c × a) = c·(a × b)

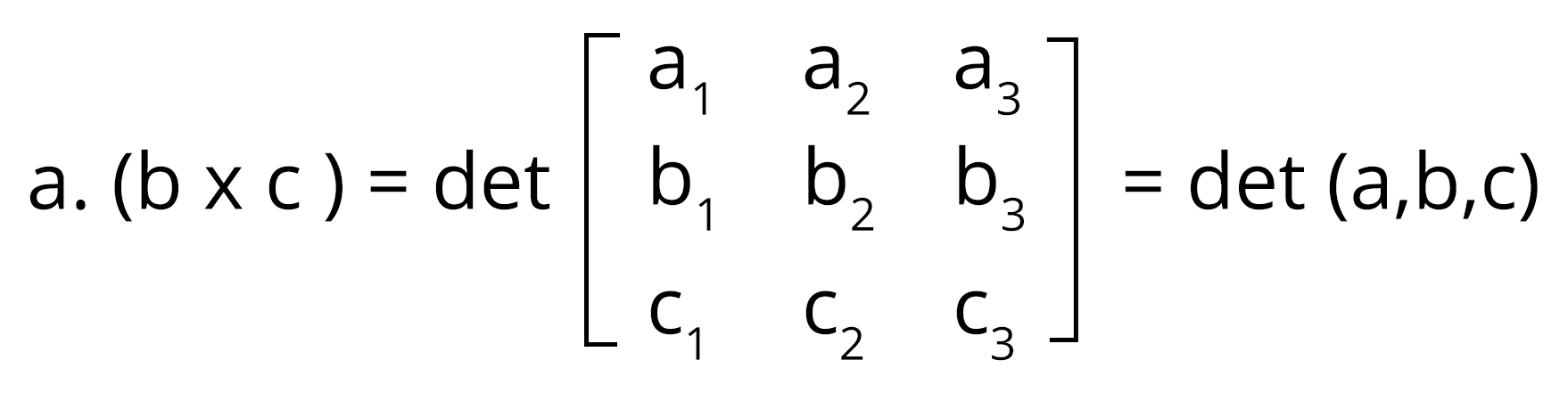
Dot Product of Vectors

To get the dot product of two vectors, multiply the individual components of the two vectors to be multiplied and add the result.

a·b = ($a_1  \hat i$ + $b_1  \hat j$ + $c_1  \hat k$) ·($a_2  \hat i$ + $b_2  \hat j$ + $c_2  \hat k$) = ($a_1, b_1, c_1$)·($a_2, b_2, c_2$) = ($a_1·a_2$) + ($b_1·b_2$) + ($c_1·c_2$)

The product of the magnitudes of the two vectors and the cosine of the angle between them is another technique to find the dot product of two vectors A and B.

$\vec{A} ·\vec{B}$ = |A||B| cosθ

The resultant of a dot product of two vectors is a scalar value, that is, it has no direction.

Cross Product of Vectors:

The vector components are represented by a matrix, and the result of the cross product of the vectors is represented by a determinant of the matrix.

$\vec{A} \times \vec{B}$ = ($b_1c_2 - c_1b_2, a_1c_2 - c_1a_2, a_1b_2 - b_1a_2$)

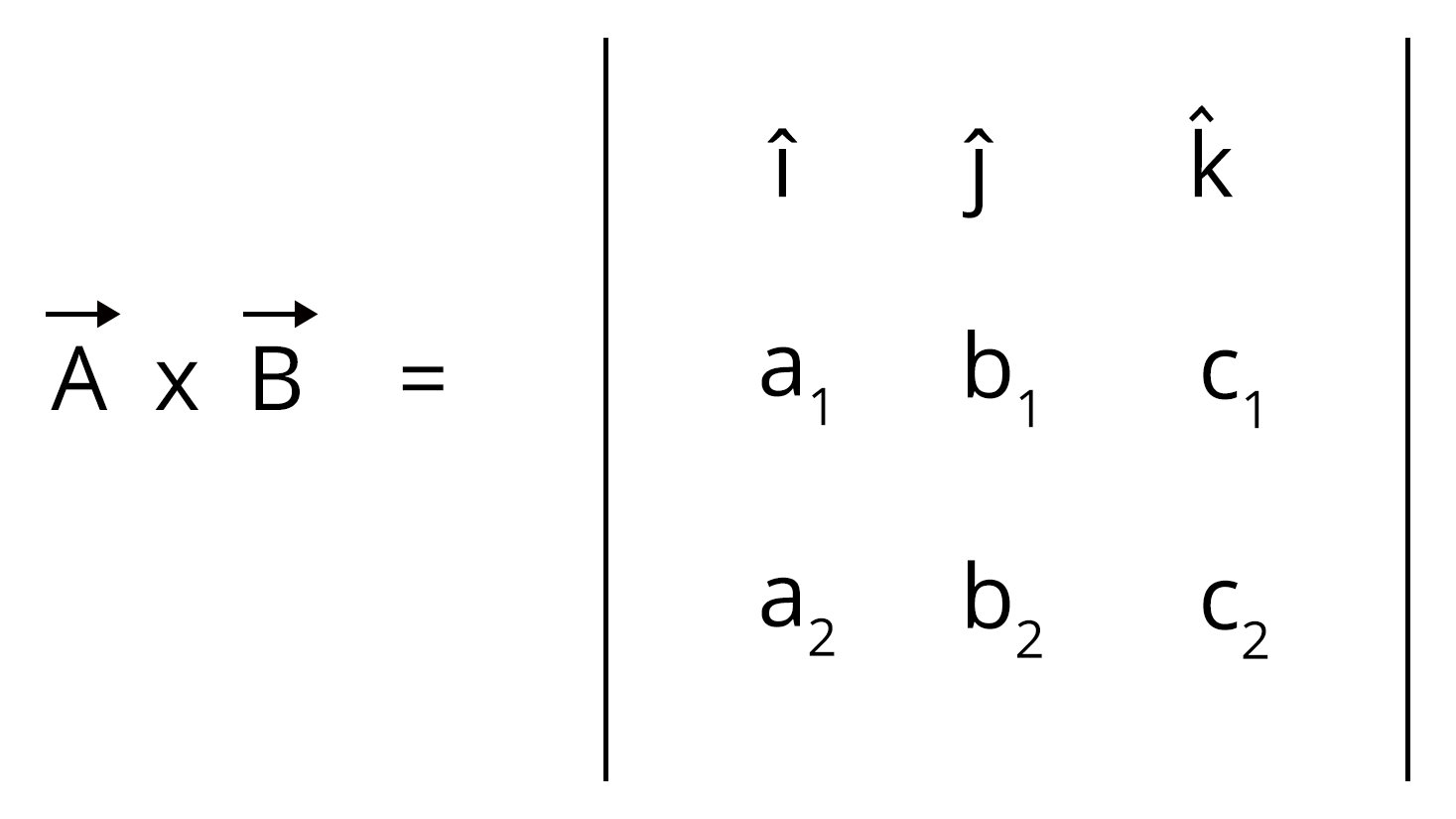
The product of the magnitudes of the two vectors and the sine of the angle between them is another technique to find the cross product of two vectors A and B.

$\vec{A} \times \vec{B}$ = |A||B| sinθ $\hat{n}$

Properties of vector 

The properties of vectors listed below helps in understanding vectors and are useful in conducting a variety of mathematical operations using vectors.

The addition of vectors is commutative and associative.

• $\vec A . \vec B = \vec B. \vec A$

• $\vec A \times \vec B\neq \vec B \times \vec A$

• $\hat i .\hat i =\hat j.\hat j = \hat k.\hat k = 1$

• $\hat i .\hat j =\hat j.\hat k = \hat k.\hat i = 0$

• $\hat i \times \hat i =\hat j\times \hat j = \hat k\times \hat k = 0$

• $\hat i \times \hat j = \hat k~;~ \hat j\times \hat k = \hat i~;~ \hat k\times \hat i = \hat j$

• $\hat j \times \hat i = -\hat k~;~ \hat k \times \hat j = -\hat i~;~ \hat i \times \hat k = -\hat j$

• The scalar dot product of two vectors lies in the plane of the two vectors and is a scalar.

• A vector that is perpendicular to the plane containing two vectors is the cross product of two vectors.

Use of Vectors

Vectors can be used to represent physical quantities. In physics, vectors are commonly employed to express displacement, velocity, and acceleration. Vectors are arrows that represent a magnitude and direction combination. The length represents the magnitude, while the vector's pointing direction represents the direction of that quantity. Because vectors are formed in this way, physical quantities (with both size and direction) can be analysed as vectors.

Applications of Vectors 

Vectors are useful in physics because they can represent location, displacement, velocity, and acceleration visually. Because you often don't have enough room to draw vectors to the scale they represent when drawing them, it's critical to know what scale you're working with. For example, consider when drawing a vector that represents a magnitude of 100, one may draw a line that is 5 units long at a scale of $\displaystyle \frac{1}{20}$. When the drawn magnitude is multiplied by the inverse of the scale, the result should equal the real magnitude.

List of Formulae

Solved Examples

Example 1: Find the sum of two vectors a = 4 $\hat i$ + 2 $\hat j$ – 5 $\hat k$ and b = 3 $\hat i$ – 2$\hat j$ + $\hat k$ ?

Solution:

Given two vectors a = 4 $\hat i$ + 2 $\hat j$ – 5$\hat k$ and b = 3$\hat i$ – 2$\hat j$ + $\hat k$

a + b = (4$\hat i$ + 2$\hat j$ – 5$\hat k$) + (3$\hat i$ – 2$\hat j$ + $\hat k$)

= (4 + 3)$\hat i$ + (2 - 2)$\hat j$ + (-5 + 1)$\hat k$

= 7$\hat i$ + 0 $\hat j$ - 4$\hat k$

= 7$\hat i$ - 4 $\hat k$

Therefore, the sum of two vectors is 7 $\hat i$ - 4 $\hat k$

Answer: 7 $\hat i$ - 4 $\hat k$

Example 2: Find the cross product of two vectors a = 4 $\hat i$ + 2$\hat j$ -5$\hat k$ and b = 3 $\hat i$ -2$\hat j$ + $\hat k$ and verify it using cross product calculator?

Solution:

Given two vectors a = 4 $\hat i$ + 2$\hat j$ – 5$\hat k$ and b = 3 $\hat i$ – 2$\hat j$ + $\hat k$

Comparing these to the vector notations we have.

a = $a_1 \hat i + a_2 \hat j + a_3 \hat k$ and b = $b_1 \hat i + b_2 \hat j + b_3\hat k$

Applying cross product formula,

a × b = $\hat i$(a2b3 − a3b2) − $\hat j$(a1b3 − a3b1) + $\hat k$(a1b2 − a2b1)

= $\hat i$((2 × 1) - (-5) × (-2)) - $\hat j$((4 × 1 - (-5) × (3)) + $\hat k$((4) × (-2) - (2 × 3))

= $\hat i$(2 - 10) - $\hat j$(4 + 15) + $\hat k$(-8 - 6)

= -8$\hat i$ - 19$\hat j$ - 14$\hat k$

Therefore, the cross product of two vectors is -8$\hat i$ - 19$\hat j$ - 14$\hat k$

Answer: -8$\hat i$ - 19$\hat j$ - 14$\hat k$

Solved problems of the Previous Year's Question Paper

Question 1: Let O be the origin and OX, OY, OZ be three unit vectors in the direction of the sides QR, RP, PQ respectively of a triangle PQR. If the triangle PQR varies, then the minimum value of cos (P+Q) + cos(Q+R) + cos (R+P) is

(a) 3/2

(b) -3/2

(c) 5/3

(d) -5/3

Solution:

In triangle PQR, P+Q+R = π

P+Q = π-R

Q+R = π-P

P+R = π-Q

cos (π-R)+ cos (π-P)+ cos (π-Q) = -cos R – cos P – cos Q

To minimize the given expression, we should maximize cos P+cos Q+cos R.

cos P+cos Q+cos R will be maximum when cos P = cos Q = cos R

=>P = Q = R = π/3

=> PQR is equilateral triangle.

So minimum value = -3 cos π/3

= -3/2

Hence option b is the answer.

Question 2: Let O be the origin and OX, OY, OZ be three unit vectors in the direction of the sides QR, RP, PQ respectively of a triangle PQR.

$\begin{array}{l}\left | \overrightarrow{OX}\times \overrightarrow{OY} \right |\end{array}$

equals

(a) sin (Q+R)

(b) sin (P+R)

(c) sin 2R

(d) sin (P+Q)

Solution:

$\begin{array}{l}\left | \overrightarrow{OX}\times \overrightarrow{OY} \right |=\left |\overrightarrow{OX} \right |\left |\overrightarrow{OY} \right |\sin \theta\end{array}$

= 1×1×sin θ

= sin (180-R)

= sin (P+Q)

Hence option d is the answer.

Question 3: Let $\begin{array}{l}\vec{a}=2\hat{i}+\lambda _{1}\hat{j}+3\hat{k}\end{array}$, $\begin{array}{l}\vec{b}=4\hat{i}+(3-\lambda _{2})\hat{j}+6\hat{k}\end{array}$ and $\begin{array}{l}\vec{c}=3\hat{i}+6\hat{j}+(\lambda _{3}-1)\hat{k}\end{array}$

be three vectors such that $\begin{array}{l}\vec{b}=2\vec{a}\end{array}$

and vector a is perpendicular to vector c. then a possible value of λ1, λ2, λ3 is

(a) (1, 3, 1)

(b) (-½, 4, 0)

(c) (½, 4, -2)

(d) (1, 5, 1)

Solution:

Given that

$\begin{array}{l}\vec{b}=2\vec{a}\end{array}$

So 4i+(3-λ2)j + 6k = 4i + 2λ1j + 6k (i, j, k are the unit vectors)

So (3-λ2) = 2λ1 ..(i)

Vector a is perpendicular to vector c.

So

$\begin{array}{l}\vec{a}.\vec{c}=0\end{array}$

6+6λ1+3(λ3-1) = 0

=> 2 + 2λ1 + λ3-1 = 0

=> λ3 = -2λ1 – 1 ..(ii)

Check the options.

(-½, 4, 0) satisfies (i) and (ii).

So possible value of λ1, λ2, λ3 are (-½, 4, 0).

Hence option b is the answer.

Practise Problems

Q1. Let $\overrightarrow{\mathrm{x}}, \overrightarrow{\mathrm{y}}$ and $\overrightarrow{\mathrm{z}}$ be three vectors each of magnitude $\sqrt{2}$ and the angle between each pair of them is $\frac{\pi}{3} .$ If $\overrightarrow{\mathrm{a}}$ is a nonzero vector perpendicular to $\overrightarrow{\mathrm{x}}$ and $\overrightarrow{\mathrm{y}} \times \overrightarrow{\mathrm{z}}$ and $\overrightarrow{\mathrm{b}}$ is nonzero vector perpendicular to $\overrightarrow{\mathrm{y}}$ and $\overrightarrow{\mathrm{z}} \times \overrightarrow{\mathrm{x}},$ then

(A) $\overrightarrow{\mathrm{b}}=(\overrightarrow{\mathrm{b}} \cdot \overrightarrow{\mathrm{z}})(\overrightarrow{\mathrm{z}}-\overrightarrow{\mathrm{x}})$

(B) $\overrightarrow{\mathrm{a}}=(\overrightarrow{\mathrm{a}} \cdot \overrightarrow{\mathrm{y}})(\overrightarrow{\mathrm{y}}-\overrightarrow{\mathrm{z}})$

(C) $\overrightarrow{\mathrm{a}} \cdot \overrightarrow{\mathrm{b}}=-(\overrightarrow{\mathrm{a}} \cdot \overrightarrow{\mathrm{y}})(\overrightarrow{\mathrm{b}} \cdot \overrightarrow{\mathrm{z}})$

(D) $\quad \vec{a}=(\vec{a} \cdot \vec{y})(\vec{z}-\vec{y})$

Answer: C

Q. Let $\Delta \mathrm{PQR}$ be a triangle. Let $\overrightarrow{\mathrm{a}}=\overrightarrow{\mathrm{QR}}, \overrightarrow{\mathrm{b}}=\overrightarrow{\mathrm{RP}}$ and $\overrightarrow{\mathrm{c}}=\overrightarrow{\mathrm{PQ}} .$ If $|\overrightarrow{\mathrm{a}}|=4 \sqrt{3}$ and $\overrightarrow{\mathrm{b} . \overrightarrow{\mathrm{c}}}=24$ then which of the following is (are) true?

(A) $\frac{|\overrightarrow{\mathrm{c}}|^{2}}{2}-|\overrightarrow{\mathrm{a}}|=12$

(B) $\frac{|\overrightarrow{\mathrm{c}}|^{2}}{2}+|\overrightarrow{\mathrm{a}}|=30$

(C) $|\overrightarrow{\mathrm{a}} \times \overrightarrow{\mathrm{b}}+\overrightarrow{\mathrm{c}} \times \overrightarrow{\mathrm{a}}|=48 \sqrt{3}$

(D) $\overrightarrow{\mathrm{a}} \cdot \overrightarrow{\mathrm{b}}=-72$

Answer: B

Conclusion

A vector is defined as an object that has both directions and magnitude in general. In this post, we'll look at several types of vectors, as well as vector operations and applications. Also, for a better grasp of the subject, we went through some of the solved examples and previous year's problems.