




How to Calculate Moment of Inertia: Formula and Step-by-Step Guide
The moment of inertia is a fundamental property in rotational mechanics, describing the resistance of an object to angular acceleration about a specified axis. It plays a crucial role in analyzing rotational motion and is central to solving problems in physics, especially in examinations like JEE Main.
Concept and Definition of Moment of Inertia
Moment of inertia, also known as rotational inertia or angular mass, quantifies the opposition of a body to changes in its rotational motion around a given axis. It depends on the mass distribution relative to the axis of rotation. When the axis or mass distribution changes, the moment of inertia also changes accordingly.
For a system consisting of discrete point masses, the moment of inertia is calculated as the sum of the products of each mass and the square of its perpendicular distance from the axis:
$I = \sum_{i} m_{i} r_{i}^{2}$
For rigid bodies with continuous mass distribution, the moment of inertia is given by the integral form:
$I = \int r^{2} \, \mathrm{d}m$
Here, $m_{i}$ represents the mass of the $i$th particle, and $r_{i}$ denotes its distance from the rotation axis. The SI unit of moment of inertia is $\mathrm{kg\,m^2}$, and its dimensional formula is $[\mathrm{M^1L^2T^0}]$.
Dependence on Axis and Mass Distribution
The value of the moment of inertia varies with the geometry of the object, the distribution of mass, and the chosen rotational axis. For objects with symmetric shapes, standard results exist for common axes, which are essential in computations and problem solving.
For additional details on related shapes, refer to Moment Of Inertia Of A Circle.
Moment of Inertia of a Hollow Sphere
Consider a thin, hollow sphere with mass $M$ and radius $R$, where mass is distributed uniformly on the surface. The moment of inertia about a diameter is derived by integrating the contributions from thin surface rings parallel to the axis.
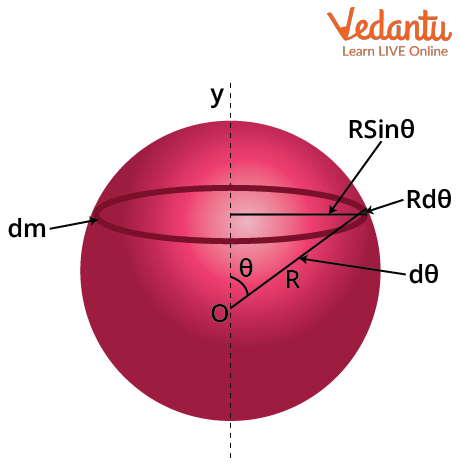
By considering the surface mass density and integrating over the angle $\theta$ from $0$ to $\pi$, the final expression for the moment of inertia is:
$I = \dfrac{2}{3}MR^{2}$
This formula shows that all mass elements reside at an equal distance from the center, contributing maximally to the moment of inertia about the diameter.
Moment of Inertia of a Solid Sphere
For a solid sphere of mass $M$ and radius $R$, the mass is distributed throughout the volume. The sphere can be considered as the combination of an infinite number of concentric hollow spheres of radii from zero to $R$.
By integrating the moment of inertia contributions of these shells, the formula obtained for the moment of inertia about the diameter is:
$I = \dfrac{2}{5}MR^{2}$
The solid sphere has a lower moment of inertia than a hollow sphere of the same mass and radius, as some mass elements are closer to the rotational axis and contribute less to the moment of inertia.
Standard Moments of Inertia for Common Shapes
Many physical systems involve simple geometric shapes. Standard moment of inertia formulas for these shapes are frequently used in calculations for various axes.
| Shape and Configuration | Moment of Inertia ($I$) |
|---|---|
| Thin Rod (axis through center, perpendicular) | $\dfrac{1}{12}ML^{2}$ |
| Thin Rod (axis through end, perpendicular) | $\dfrac{1}{3}ML^{2}$ |
| Rectangular Plate (axis through center) | $\dfrac{1}{12}M(a^{2}+b^{2})$ |
| Solid Cylinder (axis of symmetry) | $\dfrac{1}{2}MR^{2}$ |
| Solid Sphere (diameter) | $\dfrac{2}{5}MR^{2}$ |
| Hollow Sphere (diameter) | $\dfrac{2}{3}MR^{2}$ |
For more information on the derivations and properties of these shapes, visit Moment Of Inertia Of A Cube.
Integral and Parallel Axis Theorem
When the axis of rotation does not pass through the center of mass, the parallel axis theorem is applied. It states that:
$I = I_{\mathrm{cm}} + Md^{2}$
Here, $I_{\mathrm{cm}}$ is the moment of inertia about the center of mass axis, $M$ is the mass of the body, and $d$ is the perpendicular distance between the center of mass and the new axis.
Further insights on this theorem can be accessed in Understanding Moment Of Inertia.
Solved Examples on Moment of Inertia
Applying the concepts to practical examples enhances understanding and problem-solving skills for competitive exams like JEE Main. Key examples frequently involve composite objects and application of the parallel axis theorem.
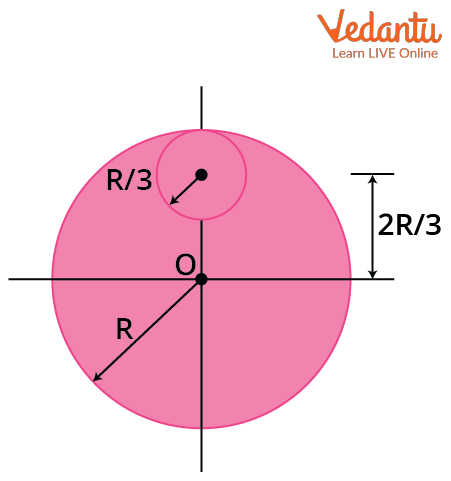
Example 1: A circular disc of radius $R$ and mass $9M$ has a small disc of radius $R/3$ removed from it. The mass of the removed disc $m$ can be found using mass density, resulting in $m = M$. The parallel axis theorem is then used to find the moment of inertia of the resulting structure about the center.
Example 2: A uniform thin wire is bent into a circle of length $L$ and mass density $\rho$. The moment of inertia of the loop about its tangent is calculated using $I = \dfrac{3}{8\pi^{2}}\rho L^{3}$, where the radius of the circle is $R = \dfrac{L}{2\pi}$.
For moment of inertia formulas for circular objects, see Moment Of Inertia Of A Disc.
Key Points on Moment of Inertia
- Moment of inertia depends on mass and its distribution
- It varies with axis orientation and geometry
- SI unit is $\mathrm{kg\,m^2}$, dimensions $[\mathrm{M^1L^2T^0}]$
- Used to calculate required torque for angular acceleration
- Integral form is essential for continuous bodies
- Parallel axis theorem is vital for non-central axes
For details on ellipses and hollow cones, refer to Moment Of Inertia Of An Ellipse and Moment Of Inertia Of Hollow Cone.
Frequently Asked Questions on Moment of Inertia
The moment of inertia is a crucial aspect of rotational dynamics in the JEE Main syllabus. It is tested directly and through related applications such as the parallel and perpendicular axis theorems. A solid sphere has a lower moment of inertia than a hollow sphere of equal mass and radius, as the solid sphere’s mass is distributed throughout its volume, resulting in lower average $r^2$ values.
FAQs on Understanding Moment of Inertia in Physics
1. What is moment of inertia?
Moment of inertia is a physical quantity that measures an object's resistance to angular acceleration around an axis.
The key points about moment of inertia are:
- It depends on the mass distribution of the object relative to the axis of rotation.
- Represented by 'I' and measured in kg·m2.
- Plays a similar role in rotational motion as mass does in linear motion.
2. What are the factors affecting moment of inertia?
The moment of inertia depends mainly on two factors:
- Mass of the body (more mass increases moment of inertia)
- Distribution of mass (farther mass is from axis, larger the moment of inertia)
3. What is the difference between mass and moment of inertia?
While both mass and moment of inertia are measures of resistance, they apply to different types of motion:
- Mass: Measures resistance to linear (straight line) acceleration.
- Moment of inertia: Measures resistance to rotational (angular) acceleration about an axis.
- Mass is scalar; moment of inertia depends on shape and axis (tensor/scalar).
4. What is the SI unit of moment of inertia?
The SI unit of moment of inertia is kilogram metre squared (kg·m2).
- This unit represents mass times the square of distance, reflecting both the mass and its distribution.
- kg·m2 is used in all standardized science exams and textbooks.
5. How is the moment of inertia calculated for different objects?
The moment of inertia for common shapes is calculated using standard formulas:
- Solid sphere: (2/5)MR2
- Thin rod (about center): (1/12)ML2
- Ring (about center): MR2
- Solid cylinder: (1/2)MR2
6. What is the physical significance of moment of inertia?
The moment of inertia determines how hard it is to start or stop an object's rotation about an axis.
- Objects with higher moment of inertia are harder to spin or stop rotating.
- It’s essential for understanding rotational motion and angular momentum.
- This concept is tested frequently in CBSE and competitive exams.
7. What is the parallel axis theorem?
The parallel axis theorem helps calculate the moment of inertia about any axis parallel to an axis through the center of mass.
- According to the theorem: I = ICM + Md2
- Here, ICM is the moment of inertia through the center of mass, M is mass, d is distance between axes.
- Used for shifting axis in CBSE rotational motion problems.
8. What is the perpendicular axis theorem?
The perpendicular axis theorem applies to flat (planar) objects and states:
The moment of inertia about an axis perpendicular to the plane is the sum of the moments of inertia about two perpendicular axes in the plane.
- Iz = Ix + Iy
- Useful for discs, plates, and CBSE exam hot topics.
9. Why does a flywheel have a large moment of inertia?
A flywheel is designed with a large moment of inertia to resist changes in rotational speed.
- Most mass is concentrated at the rim, far from the center, maximizing I = MR2.
- This helps in maintaining uniform rotation and storing energy.
10. Does moment of inertia depend on the axis of rotation?
Yes, the moment of inertia depends on the position and orientation of the axis of rotation.
- Changing the axis changes the distance of mass elements from the axis, affecting I.
- Always specify the reference axis for moment of inertia values in CBSE questions.
11. How does moment of inertia relate to angular momentum?
Angular momentum (L) is directly proportional to the moment of inertia.
- L = Iω, where ω is angular velocity.
- Higher moment of inertia leads to greater angular momentum at the same ω.
- This relationship is central in rotational dynamics and conservation laws.
12. Which has more moment of inertia: a ring or a disc (same mass and radius)?
A ring has a greater moment of inertia than a disc with the same mass and radius.
- For a ring: I = MR2
- For a disc: I = (1/2)MR2
- This is because all mass of the ring is farther from the axis.
























