




How to Add Two Simple Harmonic Motions: Method and Practice
The superposition of SHM, or superposition of simple harmonic motions, is a foundational topic in JEE Physics, explaining how multiple oscillations combine. When two or more SHMs act simultaneously, their displacements add to give a new resultant motion, impacting wave interference and sound phenomena.
Definition and Overview of Superposition Of SHM
Superposition of SHM occurs when two or more simple harmonic motions combine to result in a single motion. This is central in analyzing beats, Lissajous figures, and interference patterns in physics problems.
For example, if two tuning forks of slightly different frequencies vibrate together, the resulting motion showcases the principle of superposition. A common misconception is that amplitudes can always be added directly, but phase difference must be considered.
General Formula for Superposition Of SHM
The general equation for superposition of two SHMs along the same line and frequency is:
| Motion Equation | Meaning |
|---|---|
| y = A₁sin(ωt + φ₁) + A₂sin(ωt + φ₂) | Sum of two SHMs (same direction) |
| y = R sin(ωt + θ) | Resultant SHM form |
Resultant amplitude is given by A = √[A₁² + A₂² + 2A₁A₂cos(Δφ)]. Resultant phase is found using tanθ = (A₁sinφ₁ + A₂sinφ₂)/(A₁cosφ₁ + A₂cosφ₂). Here, Δφ = φ₂ − φ₁.
If the phase difference is zero, amplitudes add up to the maximum, but if 180°, they may cancel. In JEE, students often forget to apply the vector form, not the direct sum, for amplitude.
Superposition Of SHM: Same Line vs Perpendicular Directions
When SHMs of the same frequency act along the same line, the result is again a SHM with modified amplitude and phase. This helps explain effects seen on oscilloscopes or in sound experiments.
Superposition of SHM in perpendicular directions often generates Lissajous figures like ellipses and circles, shaped by amplitude ratios and phase difference. For example, equal amplitude and a 90° phase difference result in a circular path.
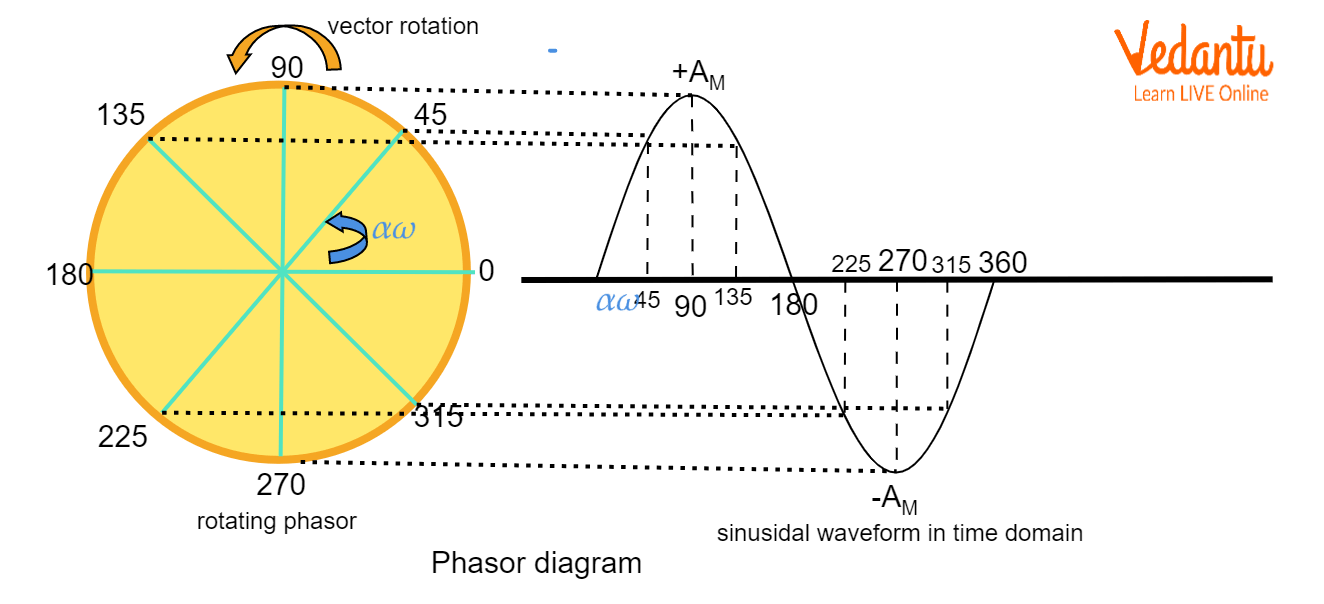
A misconception is assuming perpendicular SHMs always form circles—actual patterns depend on both frequency and phase. Visualization tools like superposition of SHM animation help build intuition.
Beats and Superposition Of SHM
When two SHMs of slightly different frequencies are superposed, the resulting motion forms beats, where amplitude varies periodically. This is key in musical tuning and analyzing sound waves.
Mathematically, if y₁ = A sin(ω₁t) and y₂ = A sin(ω₂t), the resultant is y = 2A cos[(Δω/2)t] sin[(ω_{avg})t]. The frequency of beats is |f₁ − f₂|. An example includes hearing beats when two piano notes differ slightly in frequency.
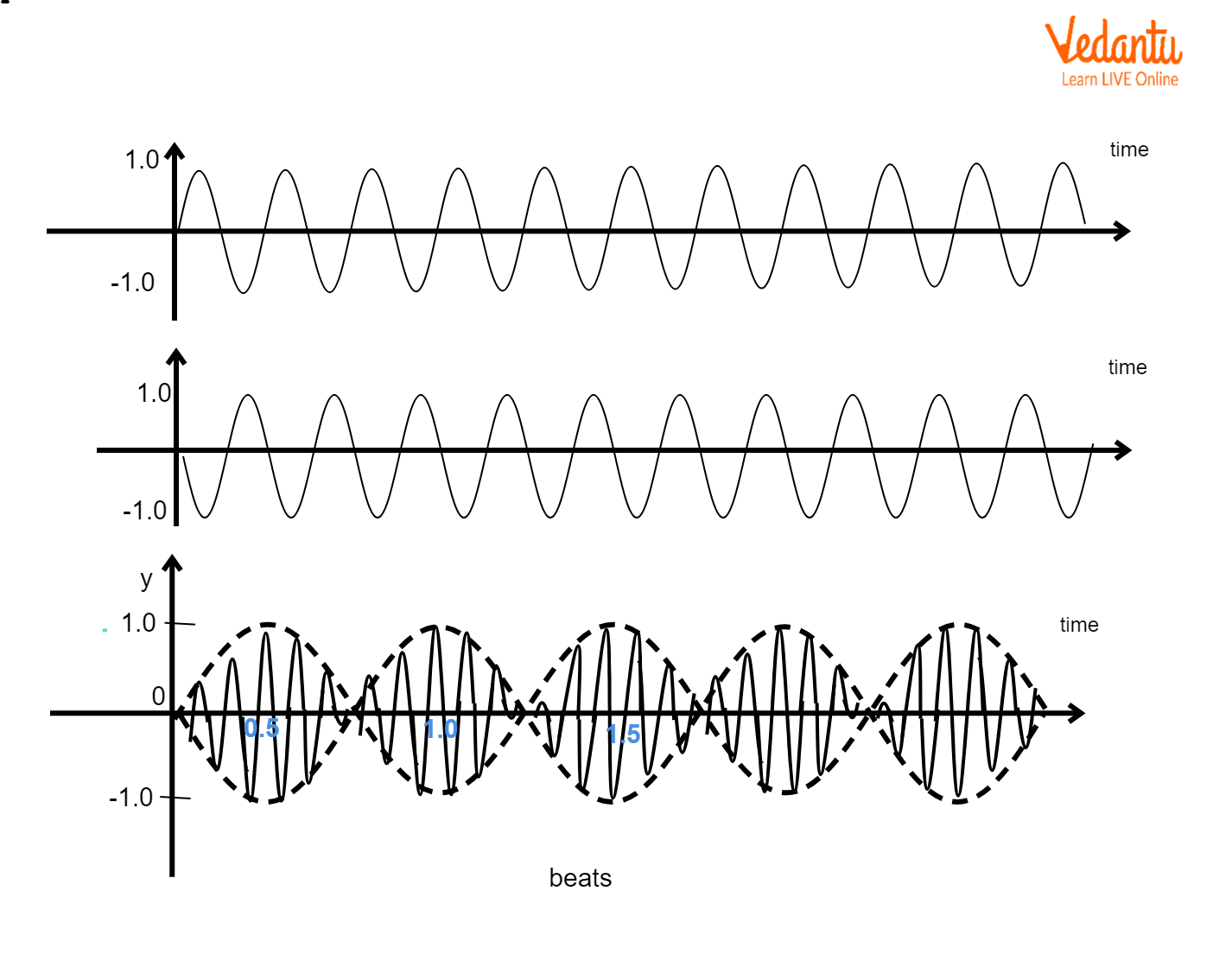
It’s a common error to confuse amplitude variation (beats) with frequency change; in reality, frequency remains the average, but amplitude oscillates.
Numerical Example: Superposition Of SHM in JEE
Consider SHMs: y₁ = 3sin(ωt) cm and y₂ = 4sin(ωt + π/2) cm. Here, the resultant amplitude is R = 5 cm, and phase = 53.13°. Resultant: y = 5sin(ωt + 53.13°) cm. Such applications are frequent in Simple Harmonic Motion based JEE questions.
If phase angles are mistakenly not converted to radians, the resultant computation will be incorrect. Always be careful with units in exam problems.
Key Takeaways: Superposition Of SHM for JEE Main
- Superposition applies only in linear systems
- Resultant amplitude depends on phase difference
- Beats form from frequency differences
- Perpendicular SHMs create Lissajous figures
- Maximum amplitude when in phase
- Zero amplitude for 180° phase difference
- Master amplitude and phase formulas for JEE
| Case | Resultant |
|---|---|
| Same frequency, same direction | SHM with new amplitude, phase |
| Slight frequency difference | Beats (Amplitude varies periodically) |
| Perpendicular directions | Lissajous figures (shapes based on phase, frequency) |
Mastering superposition of SHM simulation and equations boosts exam performance, as JEE often asks about resultant amplitudes, phases, and graphical interpretations like Lissajous figures.
FAQs on Superposition of Simple Harmonic Motions: Complete Guide
Q1. What is the superposition of SHM?
A1. It’s the process of adding two or more SHMs to generate a new collective motion, crucial for understanding beats and interference in physics.
Q2. What is the formula for the superposition of two simple harmonic motions?
A2. For two SHMs in the same direction: y = A₁sin(ωt + φ₁) + A₂sin(ωt + φ₂). Use resultant amplitude and phase formulas for solving.
Q3. When do beats form during the superposition of SHMs?
A3. Beats appear when the two SHMs have similar but not identical frequencies, causing audible oscillations in amplitude.
Q4. How does superposition of SHM work in perpendicular directions?
A4. Perpendicular SHMs generate Lissajous figures; the pattern depends on the phase difference and frequency ratio.
For more challenging practice, attempt the Oscillations And Waves Mock Test.
Q5. What is the condition for two SHMs to produce stationary waves?
A5. The two must have equal amplitude, frequency, and opposite directions, creating nodes and antinodes by constructive/destructive interference.
Q6. Can you give examples of superposition of SHMs in real life?
A6. Examples include sound interference, musical beats, and vibration patterns in structures like bridges or electronics displays.
Q7. What happens when two SHMs of equal frequency but opposite phases superimpose?
A7. When their phase difference is 180°, the result is complete destructive interference—resultant amplitude is zero.
For further reading, check out Oscillations And Waves and related topics at Vedantu.
Q8. What are common mistakes when combining SHMs with a phase difference?
A8. Failing to use correct vector addition and neglecting phase unit conversion are frequent errors; always check formulas and phase units.
Q9. How do you calculate the resultant amplitude and phase when two SHMs combine?
A9. Use: A = √[A₁² + A₂² + 2A₁A₂cos(Δφ)]; tanφ = (A₁sinφ₁ + A₂sinφ₂)/(A₁cosφ₁ + A₂cosφ₂).
Q10. Why can't superposition occur in nonlinear systems?
A10. Superposition only works in linear systems, as output directly relates to input; true for SHM but not for nonlinear responses.
Q11. Do frequencies have to be exactly the same for superposition to occur?
A11. No, but calculations are simplest when frequencies are equal or close; complex patterns appear for larger differences.
Superposition of SHM is key for analyzing wave combinations, interference, and sound phenomena like beats. Explore more about Transverse And Longitudinal Waves for complete understanding.
FAQs on Understanding Superposition of Simple Harmonic Motion
1. What is superposition of simple harmonic motions (SHM)?
The superposition of simple harmonic motions (SHM) is the combination of two or more SHMs acting simultaneously on the same particle.
Key points regarding superposition of SHM:
- It is based on the principle of superposition, allowing the resultant motion to be determined by adding individual displacements.
- The resultant motion can be another SHM or a more complex periodic motion depending on frequency, amplitude, and phase difference.
- This concept is extensively used in analysing wave interference, resonance, and beats in physics and CBSE exams.
2. What happens when two SHMs of the same frequency are superimposed?
When two SHMs of the same frequency are superimposed, their resultant motion is also a simple harmonic motion with modified amplitude and phase.
Main outcomes:
- The amplitude of the resultant SHM depends on the individual amplitudes and the phase difference between them.
- The general equation for the resultant is y = y_1 + y_2.
- If phase difference is 0 or multiples of 2π, amplitude is maximum. If it is π or an odd multiple, amplitude is minimum (possibly zero).
3. What are the conditions for constructive and destructive interference in superposition of SHM?
Constructive and destructive interference in superposition of SHM occur due to the phase difference between the motions.
Conditions:
- Constructive Interference: Occurs when the phase difference (Δϕ) is 0, 2π, 4π, etc. → Maximum amplitude.
- Destructive Interference: Occurs when phase difference (Δϕ) is π, 3π, 5π, etc. → Minimum or zero amplitude.
4. How do you find the resultant displacement when two SHMs act along the same line?
The resultant displacement is found by vector addition of the individual displacements of each SHM.
Step-by-step:
- Write equations: y_1 = A_1 sin(ωt + ϕ_1), y_2 = A_2 sin(ωt + ϕ_2)
- Add algebraically: y = y_1 + y_2
- Resultant is also of the form: y = A sin(ωt + ϕ), where A and ϕ can be determined using trigonometric identities.
5. What is the principle of superposition?
The principle of superposition states that when two or more waves overlap, the resultant displacement at any point is equal to the vector sum of the displacements due to each individual wave.
Main features:
- Applies to linear systems, including SHM and waves
- Foundation for interference, beats, and resonance
- Relevant for both physics theory and MCQ-based exams
6. Give an example where superposition of SHM occurs.
Superposition of SHM occurs in many real-life and experimental situations.
Common examples:
- Beats: When two tuning forks of slightly different frequencies are sounded together
- Standing waves: Formed on a stretched string due to superposition of two opposite SHMs
- Vibrations of air columns in organ pipes
7. What are beats and how are they related to superposition of SHM?
Beats are periodic variations in loudness caused by the superposition of two SHMs of slightly different frequencies.
Important points:
- Beat frequency = Difference between the two frequencies (f_beat = |f_1 - f_2|)
- Heard when tuning musical instruments
- Direct example of the superposition principle in sound waves
8. What results when two perpendicular SHMs are superimposed?
When two perpendicular SHMs are superimposed, the resultant motion forms a Lissajous figure.
Main details:
- Shape depends on frequency ratio and phase difference.
- If the SHMs have same frequency and zero phase difference, result is a straight line or ellipse.
- Used in analyzing waveforms on an oscilloscope.
9. How do you mathematically represent the superposition of two SHMs in the same direction?
The mathematical representation of two SHMs in the same direction is given by first writing their equations and then combining them.
Procedure:
- Write: y_1 = A_1 sin(ωt + ϕ_1), y_2 = A_2 sin(ωt + ϕ_2)
- Add: y = y_1 + y_2 = A sin(ωt + ϕ), where resultant amplitude A and phase ϕ are found using:
A = √(A_1^2 + A_2^2 + 2A_1A_2 cos(ϕ_2-ϕ_1))
10. Can superposition of SHM result in non-periodic motion?
Superposition of SHMs generally results in periodic motion, especially if the component frequencies are either same or commensurable.
Facts to note:
- If frequencies are commensurable (ratio is a rational number), the result is still periodic.
- If frequencies are incommensurable (irrational ratio), the resultant motion is not strictly periodic but is still deterministic.
























