




How Does Malus Law Describe Light Intensity Through Polarizers?
Malus Law is a fundamental concept in the study of the polarization of light, describing how the intensity of plane-polarized light changes when it passes through a polarizing filter at an angle. This law establishes the quantitative relationship between the transmitted light intensity and the angle between the polarization direction of the incident beam and the axis of the analyzer. It is essential in wave optics and finds usage in optical devices, experiments, and various competitive examinations.
Concept of Polarization and Malus Law
Polarization refers to the orientation of the oscillations of the electric field vector in an electromagnetic wave relative to its direction of propagation. When unpolarized light passes through a polarizer, only the component of the electric field aligned with the transmission axis is allowed to pass, resulting in plane-polarized light. Malus Law mathematically describes the effect of a secondary polarizer, called an analyzer, aligned at an angle with respect to the initial polarization direction.
The understanding of Malus Law is essential to explain phenomena related to the transmission and attenuation of polarized light in media and devices. Students can deepen their grasp of the topic by first reviewing the principles of Polarisation Of Light.
Mathematical Statement and Formula
Malus Law states that the intensity of polarized light transmitted through an analyzer depends on the square of the cosine of the angle between the incident light’s polarization direction and the analyzer's axis. The formula for Malus Law is expressed as:
$I = I_0 \cos^2 \theta$
Here, $I_0$ is the initial intensity of light before the analyzer, $\theta$ is the angle between the polarization direction of the incident light and the axis of the analyzer, and $I$ is the final intensity after passing through the analyzer.
Derivation of Malus Law
Consider a plane-polarized light beam incident on an analyzer at an angle $\theta$ relative to its polarization direction. The electric field vector $E_0$ of the incident light makes an angle $\theta$ with the transmission axis of the analyzer. Its component along the analyzer axis is $E_0 \cos \theta$.
The intensity of light is proportional to the square of the electric field amplitude. Thus, the transmitted intensity is:
$I \propto (E_0 \cos \theta)^2$
$I = I_0 \cos^2 \theta$
This equation confirms the mathematical relationship stated in Malus Law.
Intensity Variation: Special Cases
When the analyzer is parallel to the polarization direction ($\theta = 0^\circ$ or $180^\circ$), $\cos^2 \theta = 1$. Therefore, $I = I_0$, and all intensity is transmitted. When the analyzer is perpendicular ($\theta = 90^\circ$), $\cos^2 90^\circ = 0$, so $I = 0$, meaning no light passes through.
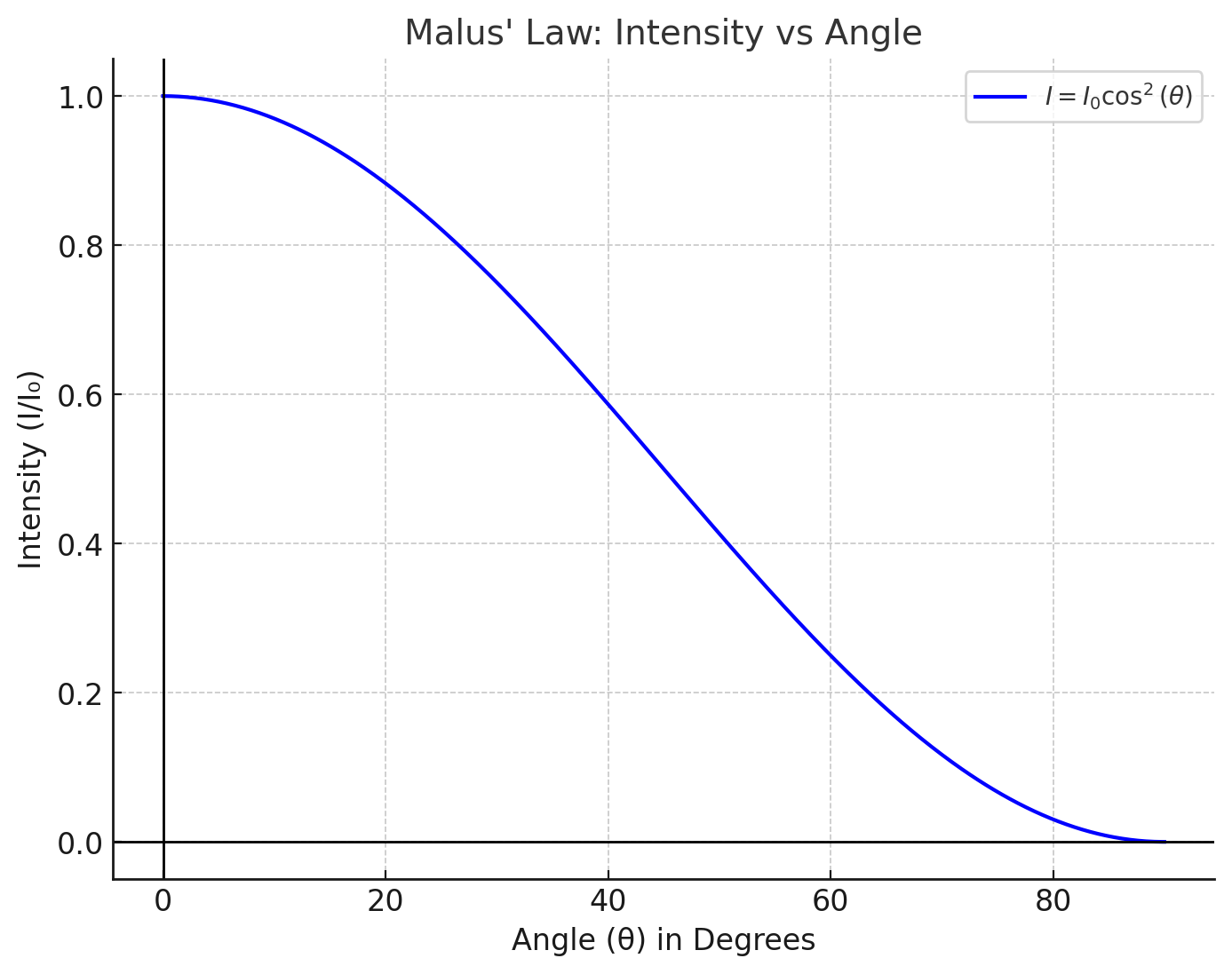
Malus Law Graph: Intensity Versus Angle
The variation of transmitted intensity with the angle $\theta$ is represented graphically as a cosine squared curve. The maximum intensity occurs at $0^\circ$ and $180^\circ$, while zero occurs at $90^\circ$ and $270^\circ$.
Application of Malus Law
Malus Law is widely applied in analyzing the behavior of polarized light in various devices and experimental setups. Its importance extends to technological and scientific fields involving optical filters.
- Verification of polarization in optical experiments
- Design of anti-glare sunglasses and filters
- Measurement of polarization states in laboratories
- Control of light intensity in photographic instruments
- Analysis of stress patterns in transparent materials
To further relate this concept to wave phenomena, refer to the explanations on the Wave-Particle Duality page.
Comparison: Malus Law and Brewster Law
| Malus Law | Brewster Law |
|---|---|
| Governs intensity transmission through a polarizer | Determines angle for maximum polarization by reflection |
| $I = I_0 \cos^2 \theta$ | $n = \tan \theta_B$ |
| Applies to polarized light and polarizer arrangements | Applies to light reflection at an interface |
Malus Law for Unpolarized Light
When unpolarized light passes through a polarizer, only the component aligned with the transmission axis is transmitted. The average value of $\cos^2 \theta$ over all possible angles is $\dfrac{1}{2}$, so the transmitted intensity becomes $I = \dfrac{I_0}{2}$ after the first polarizer. Malus Law is then applied to further polarizers for the remaining beam.
Malus Law for Multiple Polarizers
For light passing through more than two polarizers, the intensity after each analyzer is obtained by successive application of Malus Law. For example, with three polarizers, the transmitted intensity is given by $I = \dfrac{I_0}{2} \cos^2\theta_1 \cos^2\theta_2$, where $\theta_1$ and $\theta_2$ are the angles between the transmission axes of consecutive polarizers.
Solved Example: Using Malus Law
A beam of plane-polarized light of intensity $8\,\mathrm{W/m^2}$ is incident on a polarizer oriented at $60^\circ$ to the beam's polarization direction. Calculate the intensity after the polarizer.
Given $I_0 = 8\,\mathrm{W/m^2}$, $\theta = 60^\circ$; using $I = I_0 \cos^2 \theta$:
$\cos 60^\circ = 0.5 \implies \cos^2 60^\circ = 0.25$
$I = 8 \times 0.25 = 2\,\mathrm{W/m^2}$
Critical Points and Common Mistakes
- The angle $\theta$ is always between polarization direction and analyzer axis
- Malus Law does not apply directly to unpolarized light; halve intensity first
- Always use $\cos^2 \theta$ in calculations
- No light is transmitted if polarizer and analyzer are perpendicular
Reviewing the concept of the Huygens Principle can reinforce foundational knowledge in wave optics, supporting the understanding of polarization and related laws.
FAQs on Understanding Malus Law in Physics
1. What is Malus Law?
Malus Law states how the intensity of polarized light changes when it passes through a polarizer at an angle to its plane of polarization.
- Intensity (I) = I0 cos²θ, where I0 is initial intensity and θ is the angle between the light’s polarization direction and polarizer axis.
- Explains the relationship between light intensity and angle of analyzer.
- Frequently asked in CBSE Physics exams (Class 12, Chapter: Wave Optics).
2. State Malus Law in physics.
Malus Law states that the intensity of plane polarized light after passing through an analyzer is directly proportional to the square of the cosine of the angle between the transmission axis of the analyzer and the initial polarization direction.
- Mathematically: I = I0 cos²θ.
- Shows how the intensity varies with rotating the analyzer.
3. What is the formula of Malus Law?
The formula for Malus Law is I = I0 cos²θ.
- I = transmitted intensity
- I0 = initial intensity of polarized light
- θ = angle between incident light polarization and analyzer axis
4. What are the applications of Malus Law?
Malus Law has various applications in optics and physics experiments:
- Design of polaroid sunglasses to reduce glare
- Optical instruments like polarimeters
- Photography for controlling light intensity
- LCD technology
- Measuring degree of polarization
5. Explain the importance of Malus Law in wave optics.
Malus Law is crucial in wave optics as it quantitatively describes light polarization phenomena.
- Predicts intensity changes when light passes through polarizers.
- Validates the nature of transverse waves.
- Helps students solve numerical and conceptual problems involving polarized light.
6. What happens when θ = 90° according to Malus Law?
When θ = 90°, cos²(90°) = 0, so the transmitted intensity I becomes zero.
- No light passes through the analyzer when its axis is perpendicular to the light’s initial polarization direction.
7. Why is Malus Law not applicable to unpolarized light?
Malus Law specifically applies to plane polarized light, not unpolarized light.
- Unpolarized light has vibrations in all directions perpendicular to the direction of propagation.
- When unpolarized light passes through a single polarizer, it becomes polarized and loses half its intensity (I = I0/2), not following the cos²θ law right away.
8. Who discovered Malus Law and in which year?
Malus Law was discovered by Etienne-Louis Malus, a French physicist, in 1809.
- His work established the mathematical relationship between light intensity and the polarization angle.
9. Derive the Malus Law for intensity of polarized light.
To derive Malus Law:
- Consider plane polarized light incident on a polarizer (analyzer) at angle θ to the polarization direction.
- The electric field component along analyzer's axis: E = E0 cosθ.
- Intensity is proportional to square of electric field amplitude, so I ∝ (E0 cosθ)² = E0² cos²θ.
- Thus, I = I0 cos²θ.
10. What is the significance of angle θ in Malus Law?
The angle θ in Malus Law determines how much polarized light intensity passes through the analyzer.
- At θ = 0°, I = I0, maximum intensity.
- At θ = 90°, I = 0, complete extinction.
- At θ = 45°, I = I0/2.
11. State and prove Malus Law. (CBSE/NCERT FAQ, Class 12)
Statement: Malus Law states that when plane polarised light is incident on an analyser, the transmitted intensity varies as the square of the cosine of the angle between the transmission axis of the analyzer and the plane of polarization.
Proof:
- Let initial intensity be I0.
- Let θ be the angle between transmission axis and plane of polarization.
- Component of electric field along axis: E = E0 cosθ.
- Intensity ∝ (Electric field)2, so I = I0 cos²θ.

















