



Mastering JEE Main Concepts of Limits, Continuity and Differentiability
When we talk about calculus, we frequently notice that limits and continuity have a distinct and essential position due to their extremely different and important notions. The term limit, on the one hand, refers to the number that a function approaches, whereas the term function can be continuous or discontinuous. Positive discontinuity, Jump discontinuity, and Infinite discontinuity are the three types of discontinuity that fit into this category. We'll go through this topic in-depth with the help of solved examples in this part.
JEE Main Maths Chapters 2024
Important Topics of Maths Limit, Continuity and Differentiability Chapter
Limits and Derivatives
Evaluating Limit
Algebra of limits
L’Hospital Rule
Function
Continuity and Differentiability
Continuity and Differentiability Properties and Formula
Limits Properties and Formula
Intermediate Value Theorem
Application of Derivatives
Maxima and Minima
Rolle’s Theorem and Lagrange’s Mean Value Theorem
Maths Limit, Continuity and Differentiability Important Concepts For JEE Main
What are Limits?
The value obtained by a function f(x) at a point x=a is the value obtained by the function at a point very close to x=a.
Consider the limit of a real-valued function ‘f’ and a real number ‘a’, which is generally say that, \[\underset{x \to a}{\lim} f(x) = L\] if there is a number $\delta$ for every number $\epsilon$ such that $|f(x)-L| < \epsilon$ whenever $0 < |x-a| < \delta$
Existence of Limit, Left Hand Limit and Right Hand Limit - Types of Limits
Left Hand Limit - When a limit is described in terms of a number smaller than a, it is referred to as a left hand limit. It's written as $x \to a^{-}$, which is the same as $x=a-h$ with $h > 0$ and $h \to 0$.
Right Hand Limit - When a limit is described in terms of a number greater than a, it is referred to as a right hand limit. It is written as $x \to a^{+}$, which is the same as $x=a+h$ with $h > 0$ and $h \to 0$.
Existence of Limit - A function's limit at $x = a$ exists only if both its left and right hand limits exist, are equal, and have a finite value, i.e., $\underset{x \to a^{-}}{\lim} f(x) = \underset{x \to a^{+}}{\lim} f(x)$
Limits and Functions
A function may reach one of two limits. One in which the variable approaches its limit by taking values that are greater than the limit, and the other in which the variable approaches its limit by taking values that are smaller. The limit is not stated in this situation, although the right and left-hand limitations do exist.
When the $\underset{x \to a}{\lim} f(x) = A^{+}$ is used, the values of f near x to the right of ‘a’ are used. The right hand limit of f(x) at ‘a’ is stated to be this value.
When the $\underset{x \to a}{\lim} f(x) = A^{-}$ is used, the values of f near x to the left of ‘a’ are used. The left hand limit of f(x) at ‘a’ is referred to as this value.
The function’s limit exists if and only if the left-hand limit is equal to the right-hand limit.
List of Important Formulas For Maths Limits Chapter
$\underset{x \to 0}{\lim} \dfrac{\sin x}{x}=1$
$\underset{x \to 0}{\lim} \cos x=1$
$\underset{x \to 0}{\lim} \dfrac{\tan x}{x}=1$
$\underset{x \to 0}{\lim} \dfrac{1-\cos x}{x}=0$
$\underset{x \to 0}{\lim} \dfrac{\sin x^{\circ}}{x}=\dfrac{\pi}{180}$
$\underset{x \to a}{\lim} \dfrac{x^{n}-a^{n}}{x-a}=n a^{n-1}$
$\underset{x \to \infty}{\lim}\left(1+\dfrac{k}{x}\right)^{m x}=e^{m k}$
$\underset{x \to 0}{\lim}(1+x)^{\dfrac{1}{x}}=e$
$\underset{x \to 0}{\lim} \dfrac{\left(a^{x}-1\right)}{x}=\ln a$
$\underset{x \to 0}{\lim} \dfrac{e^{x}-1}{x}=1$
$\underset{x \to 0}{\lim} \dfrac{\ln (1+x)}{x}=1$
$\underset{x \to \infty}{\lim} x^{\dfrac{1}{x}}=1$
Maths Limits Points to Remember
If \[\lim_{x\rightarrow k^{-}} f(x)\] is the expected value of f at x = k stated the values of ‘f’close by x to the left side of k. This value is determined as the left-hand limit of ‘f’ at k.
If \[\lim_{x\rightarrow k^{+}} f(x)\] is the average value of f at x = k stated the values of ‘f’ close by x to the right side of k This value is determined as the right-hand limit of f(x) at k.
If the right-hand and left-hand limits meet each other, we state the common value as the limit of f(x) at x = k and represent it by \[\lim_{x\rightarrow k} f(x)\].
One-Sided Limit
The limit that relies completely on the values of a function considered at x -value that is moderately greater or less than a particular value. A two-sided limit \[\lim_{x\rightarrow k} f(x)\] considers the values of x into account that are both larger than and smaller than k. A one-sided limit from the left side \[\lim_{x\rightarrow k^{-}} f(x)\] or from the right side \[\lim_{x\rightarrow k^{+}} f(x)\] considers only values of x that are smaller or greater than k respectively.
Properties of Limit
The limit of a function is defined as f(x) as approaches K as x inclines to limit y, such that; \[\lim_{x\rightarrow y} f(x) = k\].
The limit of the addition of two functions is equivalent to the addition of their limits, such that \[\lim_{x\rightarrow y}[f(x) + g(x)] = \lim_{x\rightarrow y}f(x) + \lim_{x\rightarrow y} g(x)]\]
The limit of any constant function will be the constant term, such that, \[\lim_{x\rightarrow y} C = C\].
The limit of multiplication of the constant and function is equivalent to the multiplacation of constant and the limit of the function, such that: \[\lim_{x\rightarrow y}m f(x) = m \lim_{x\rightarrow y}f(x)\].
Quotient Rule of the limit of a function: \[\lim_{x\rightarrow y}[\dfrac{f(x)}{g(x)}] = \dfrac{\lim_{x\rightarrow y}f(x)}{\lim_{x\rightarrow y}g(x)}\], if \[\lim_{x\rightarrow y}g(x) = 0\].
Evaluation of Algebraic Limits
Sometimes, when we look at a mathematical function, it can seem like it's heading towards infinity or a really big number as we get closer to a certain point. For example, if we're looking at the function 1 divided by the absolute value of x, as x gets closer and closer to 0, the result gets bigger and bigger, almost like it's going to infinity.
Some of the methods of evaluating limits include:
Direct Substitution Method:
If we want to know the limit of a function as it approaches a certain point 'a,' we can simply plug in 'a' and see what value we get. If the function and some related expressions are all fixed at 'a,' then the limit is just the value we get by plugging in 'a.'
Consider the following limits (i) limx→a f(x) and (ii) limx→a φ(x)/Ψ(x).
If f(a) and φ(a)/Ψ(a) exist and are fixed real numbers and Ψ(a) ≠ 0, then we say that limx→a f(x) = f(a) and limx→a φ(x)/Ψ(x) = φ(a)/Ψ(a).
Factorization Method:
When we try the direct substitution method, we end up with a tricky situation where we get 0 divided by 0. In such cases, we can use factorization. We break down the function into smaller pieces and see if there's something common in both the numerator and denominator that we can cancel out.
Consider limx→a f(x)/g(x). If by substituting x = a, f(x)/g(x) reduces to the form 0/0, then (x-a) is a factor of both f(x) and g(x). So, we first factorize f(x) and g(x) and then cancel out the common factor to evaluate the limit.
Rationalization Method:
This method is generally used in cases where either the numerator or the denominator or both involve expression consists of square roots and on substituting the value of x, the rational expression takes the form 0/0, ∞/∞.
Evaluation of Algebraic limits at infinity:
When we're dealing with really large numbers, like when 'x' goes to infinity, we can use some known limits, like the limit of $\dfrac{1}{x}$ or $\dfrac{1}{x^2}$, to figure out what's happening. For example,
We know that $\lim_{x\to \infty} \dfrac{1}{x}=0$ and $\lim_{x\to \infty} \dfrac{1}{x^2}=0$.
Then $\lim_{x\to \infty} f(x) = \lim_{y\to 0} f\left(\dfrac{1}{y}\right)$.
Limits using Sandwich Theorem:
Sometimes, it's hard to directly figure out the limit. In such cases, we can use a handy theorem called the Sandwich Theorem. It tells us that if we have three functions, and we know that one is always smaller than another and they all approach the same limit, then the middle one approaches that same limit too.
Let f(x), g(x) and h(x) be three real numbers having a common domain D such that h(x) ≤ f(x) ≤ g(x) ∀ x ∈ D. If limx→a h(x) = limx→a g(x) = l, then limx→a f(x) = l. This is known as Sandwich Theorem.
L’Hospital Rule
If the supplied limit $\underset{x \to a}{\lim} \dfrac{f(x)}{g(x)}$ is of the form $\dfrac{0}{0}$ or $\dfrac{\infty}{\infty}$, that is, both f(x) and g(x) are 0 or both f(x) and g(x) are infinity, then the limit can be solved using the L'Hospital Rule that is,
$\underset{x \to a}{\lim} \dfrac{f(x)}{g(x)} = \underset{x \to a}{\lim} \dfrac{f^\prime(x)}{g^\prime(x)}$, where $f^\prime(x)$ and $g^\prime(x)$ is obtained by differentiating f(x) and g(x).
What is Continuity and Differentiability?
The continuity of a function and the differentiability of a function are mutually exclusive. Before it can be shown for its differentiability at x = a, the function y = f(x) must first be proved for its continuity at x = a. Both continuity and differentiability can be demonstrated geometrically and algebraically.
Continuity of a Function
The graph y = f(x) of a function is said to be continuous over a range if it is a single unbroken curve (the graph can be drawn easily without lifting the pencil at a point).
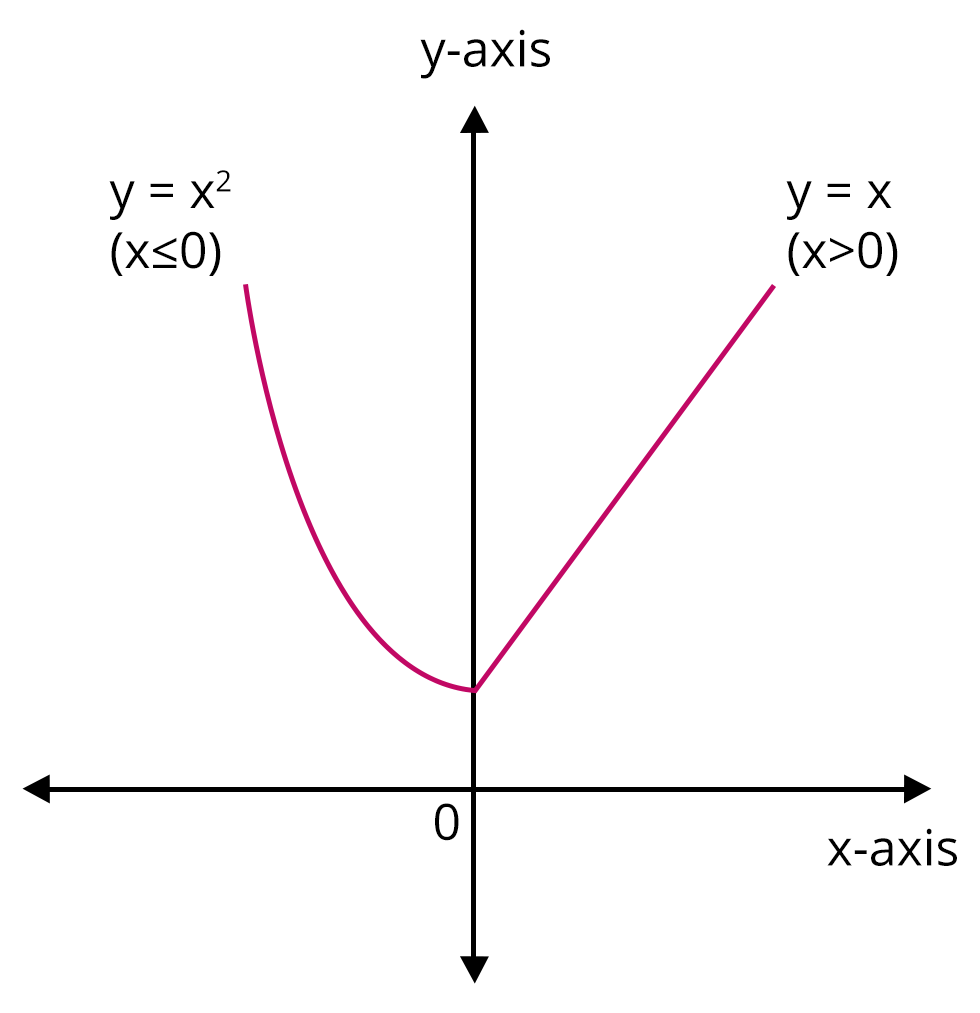
Graph of function y = f(x)
Technically we can say that, a continuous real valued function f(x) exists and is equal to $f(x_0)$ at a point $x=x_0$ in the domain if $\underset{x \to x_0}{\lim} f(x)$ exists and is equal to $f(x_0)$.
If a function f(x) is continuous at $x=x_0$, then $\underset{x \to x_0^{+}}{\lim} f(x) = \underset{x \to x_0^{-}}{\lim} f(x) = \underset{x \to x_0}{\lim} f(x)$
Discontinuous functions are those that are not continuous.
Types of Discontinuity
Infinite Discontinuity:
A division of discontinuity in which a vertical asymptote exists at x = a and f(k) is not defined. This is also known as asymptotic discontinuities. If a function possesses values on both sides of an asymptote, then it cannot be interlinked, so it is discontinuous at the asymptote.
Jump Discontinuity:
A division of discontinuity in which \[\lim_{x\rightarrow k^{+}} f(x) = \lim_{x\rightarrow k^{-}} f(x)\] but the limit present on both sides are finite.This is also known as simple discontinuity or continuities of the first kind.
Positive Discontinuity:
A division of discontinuity in which function has a predetermined two-sided limit at x = k but either f(x) is not defined at ‘k’ or its value is not equivalent to the limit at k.
Properties of Continuous Functions:
Existence of Limit: A function f(x) is continuous at a point a if and only if the limit of f(x) as x approaches a exists, and the limit is equal to f(a).
Algebraic Operations: Continuous functions satisfy algebraic operations. That is, if f(x) and g(x) are continuous functions at a point a, then their sum, difference, product, and quotient (as long as the denominator is not zero) are also continuous at a.
Compositions of Continuous Functions: If f(x) is continuous at a, and g(x) is continuous at f(a), then the composition g(f(x)) is continuous at a.
Continuity Over an Interval: A function f(x) is continuous on a closed interval [a,b] if it is continuous at every point within the interval (a,b), and it is continuous from the right at a and from the left at b.
Intermediate Value Theorem (IVT): If f(x) is a continuous function on a closed interval [a,b], and y is any number between f(a) and f(b), then there exists at least one c in the interval [a,b] such that f(c)=y. In other words, the function takes on all values between f(a) and f(b) on the interval.
Extreme Value Theorem (EVT): If f(x) is a continuous function on a closed interval [a,b], then it has both a maximum and a minimum value on that interval. In other words, there exist c and d in [a,b] such that f(c) is the maximum value, and f(d) is the minimum value.
Bolzano-Weierstrass Theorem: If a sequence of real numbers is bounded and monotonically increasing or decreasing, then it has a limit, and that limit is a real number. This property is often used to prove the existence of limits for continuous functions.
Uniform Continuity: A function f(x) is uniformly continuous on an interval [a,b] if, for any given ϵ > 0, there exists a δ>0 such that for all x and y in the interval [a,b] with ∣x−y∣<δ, it follows that ∣f(x)−f(y)∣<ϵ. This is a stronger form of continuity compared to the usual definition of continuity.
Common Functions and their Continuous Intervals:
Functions that are commonly used, along with the specific ranges or intervals where they stay smooth and uninterrupted.
Differentiability of A Function
The derivative of a real valued function f(x) with respect to x if the derivative $f^\prime(a)$ exists at every point in its domain, which is defined as
$\underset{h\to 0}{\lim} \dfrac{f(x+h)-f(x)}{h}$
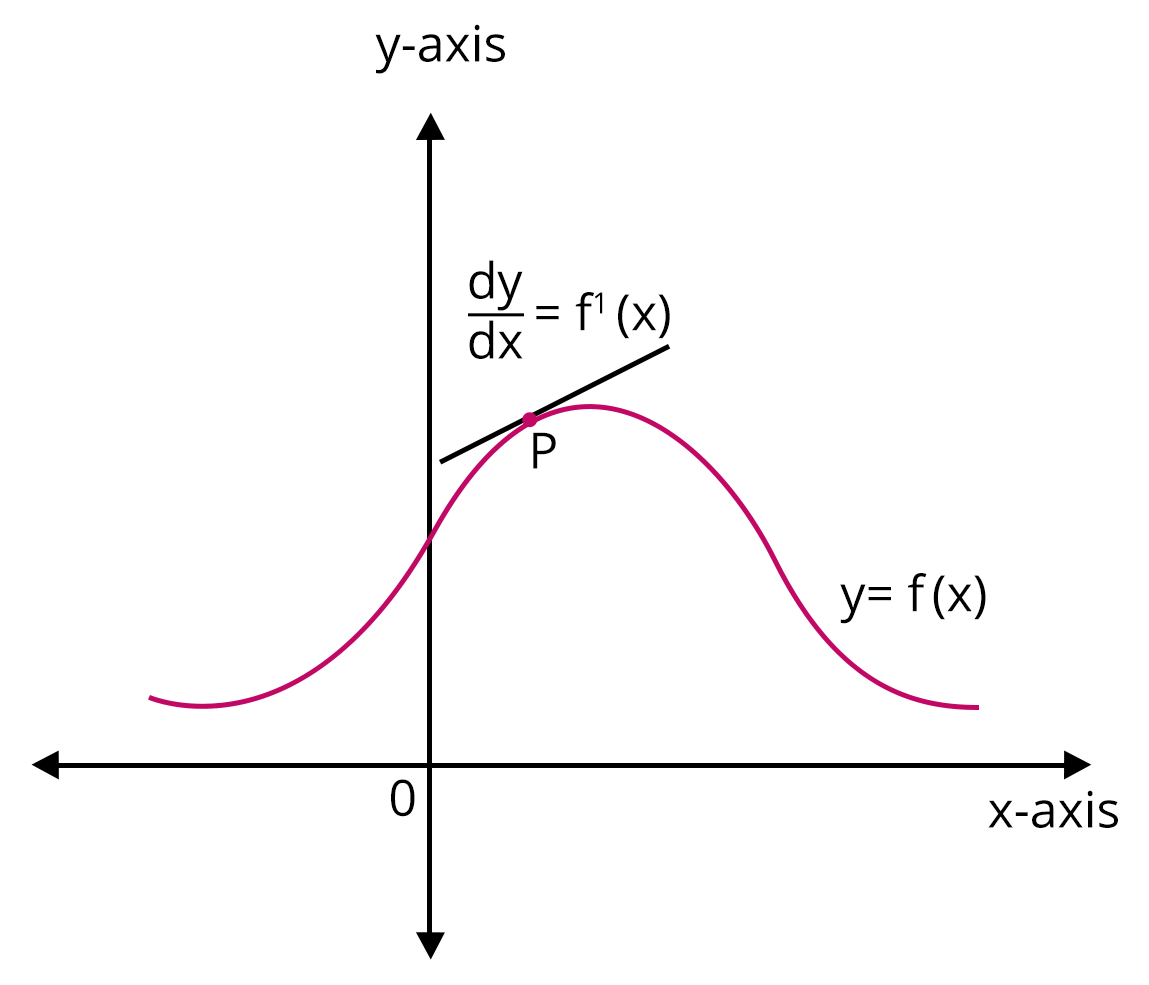
Derivative of a function f(x)
If the derivative of a function exists at all points in its domain, the function is said to be differentiable. To test the differentiability of a function at x=c, $\underset{h\to 0}{\lim} \dfrac{f(c+h)-f(c)}{h}$ must exist.
Thus we can say that every differentiable function is continuous
Note: If a function is differentiable at a given point, it is also continuous at that same point. But just because a function is continuous at a point doesn't mean it's also differentiable at that point.
Important Differentiation of the Functions
Derivative of Composite Function
In Layman’s terms, to differentiate a composite function at any point in its domain, first differentiate the outer part (i.e., the function enclosing some other function) and then multiply it with the inner function’s derivative function. This will provide us with the desired differentiation.
Derivatives of Implicit Functions
When the dependent variable in a function is not explicitly isolated on either side of the equation, the function is referred to as an implicit function.
Derivatives of Inverse Trigonometric Functions
The derivatives of inverse trigonometric functions are known as inverse trigonometric derivatives. The inverses of the six basic trigonometric functions are called inverse trigonometric functions. Inverse trigonometric derivatives are defined only in the domain of inverse trigonometric functions, as follows:
Inverse Trigonometric Function | Domain |
arcsin x | $\left[-1, 1\right]$ |
arccos x | $\left[-1, 1\right]$ |
arctan x | R |
arccosec x | $(-\infty, -1] \cup [1, \infty)$ |
arcsec x | $(-\infty, -1] \cup [1, \infty)$ |
arccot x | R |
Derivatives of Exponential Functions
The product of the exponential function ax and the natural log of a, $f^\prime(x) = ax~ln ~a$, is the derivative of the exponential function $f(x) = ax$, $a > 0$. The exponential function's derivative is written as $\dfrac{d(ax)}{dx} = (ax)^\prime = ax~ln~a$. The first principle of differentiation and the formulas of limits can be used to calculate the derivative of an exponential function. When $a > 1$ and when $a < 1$, the graph of the exponential function's derivative changes direction.
Formula for derivative of exponential function is given as,
$f(x) = ax, f^\prime(x) = ax~ln~a$ or $\dfrac{d(ax)}{dx} = ax~ln~a$
$f(x) = ex, f^\prime(x) = ex$ or $\dfrac{d(ex)}{dx} = ex$
Derivatives of Logarithmic Functions
The slope of the tangent to the curve representing the logarithmic function is determined by the logarithmic function's derivation. The following is the formula for the derivative of the common and natural logarithmic functions.
$\dfrac{1}{x}$ is the derivative of $ln x$. For example, $\dfrac{d}{dx} \dfrac{1}{x} = ln x$
$\dfrac{1}{x(x ~log~ a)}$ is the derivative of $log_a x$
Derivatives of Functions in Parametric Forms
There are times when we define a function using the third variable rather than explicitly or implicitly defining it. This is a parametric form, which is when a function y(x) is represented by a third variable called the parameter.
$\dfrac{d^2y}{dx^2} = \dfrac{d}{dx}\left(\dfrac{dy}{dx}\right) = \dfrac{\dfrac{d}{dt} \left(\dfrac{dy}{dx}\right)} {\dfrac{dx}{dt}}$
List of Important Formulae of Maths Continuity and Differentiability Chapter
1. $f(x)$ is continuous at $x=a$ if $\lim _{x \rightarrow a-} f(x)=\lim _{x \rightarrow a+} f(x)=f(a)$
2. $\dfrac{d}{d x}\left(x^{n}\right)=n x^{n-1}$ i.e $\dfrac{d}{d x}(\mathrm{x})=1$.
3. $\dfrac{d}{d x}(\sin x)=\cos x$.
4. $\dfrac{d}{d x}(\cos x)=-\sin x$.
5. $\cdot \dfrac{d}{d x}(\tan x)=\sec ^{2} x .$
6. $\dfrac{d}{d x}(\cot x)=-\operatorname{cosec}^{2} x$.
7. $\dfrac{d}{d x}(\sec x)=\sec x \tan x$.
8. $\dfrac{d}{d x}(\operatorname{cosec} x)=-\operatorname{cosec} x \cot x$.
9. $\dfrac{d}{d x}\left(\sin ^{-1} x\right)=\dfrac{1}{\sqrt{1-x^{2}}}$
10. $\dfrac{d}{d x}\left(\cos ^{-1} x\right)=-\dfrac{1}{\sqrt{1-x^{2}}}$
11. $\dfrac{d}{d x}\left(\tan ^{-1} x\right)=\dfrac{1}{1+x^{2}}$
12. $\dfrac{d}{d x}\left(\cot ^{-1} x\right)=-\dfrac{1}{1+x^{2}}$.
13. $\dfrac{d}{d x}\left(\sec ^{-1} x\right)=\dfrac{1}{x \sqrt{x^{2}-1}}$
14. $\dfrac{d}{d x}\left(\operatorname{cosec}^{-1} x\right)=-\dfrac{1}{x \sqrt{x^{2}-1}}$
To understand the principles of continuity and differentiability, students should become familiar with the relevant mathematical formulas.
Theorems on Continuity and Differentiability
Theorem 1: If two functions f(x) and g(x) are continuous at a real valued function and continuous at a point x = c, we have:
At the point $c = c$, $f(x) + g(x)$ is continuous.
At $x = c$, $f(x) - g(x)$ is continuous.
Also at $x = c$, $g(x) \cdot g(x)$ is continuous.
At $x = c$, $\dfrac{f(x)}{g(x)}$ is continuous if $g(c) \neq 0$.
Theorem 2: The composite function fog(x) is defined at x = c for two real-valued functions f(x) and g(x). If the function f(x) is continuous at g(c) and g(x) is continuous at x = c, then fog(x) is continuous at x = c.
Theorem 3: If a function f(x) is differentiable at x = c, it is also continuous at that point. Every differentiable function is continuous, in other words.
Theorem 4: Chain Rule - $f = vou$ for a real-valued function f(x) is a composite of two functions u and v. Also, if $t = u(x)$ and both $\dfrac{dt}{dx}$ and $\dfrac{dv}{dt}$ exist, then $\dfrac{df}{dx} = \dfrac{dv}{dt}\cdot dt \cdot dx$ is obtained.
Theorem 5: The derivative of $e^x$ with respect to $x$ is $e^x$. And the derivative of $log x$ with respect to $x$ is $\dfrac{1}{x}$.
Theorem 6: Rolle's Theorem - If a function f(x) is continuous across the interval $\left[a, b\right]$ and differentiable across the interval (a, b), such that f(a) = f(b), and a, b are some real numbers. Then there exists a point c in the interval $\left[a, b\right]$ such that $f^\prime(c) = 0$.
Theorem 7: Mean Value Theorem - If a function f(x) is continuous across the interval $\left[a, b\right]$ and differentiable across the interval (a, b), then there exists a point c in the interval $\left[a, b\right]$ such that $f^\prime(c) = \dfrac{f(b) - f(a)}{b - a}$.
Applications of Derivatives:
1. Rate of Change Formula
The rate of change function represents the rate at which one quantity changes in relation to another. Simply put, the rate of change is the difference between the amount of change in one item and the corresponding amount of change in another.
i.e., $\dfrac{\Delta y}{\Delta x} = \dfrac{y_2 - y_1}{x_2 - x_1}$
For a linear function
$\dfrac{\Delta y}{\Delta x} = \dfrac{f(b) - f(a)}{b - a}$
Note:
The rate of change of quantity, $\dfrac{dy}{dx}$, is represented by a positive sign when it increases.
The rate of change of quantity, $\dfrac{dy}{dx}$, is represented by a negative sign when it decreases.
2. Increasing and Decreasing Functions
If the value of y increases as the value of x increases, then the function $y = F(x)$ is known as an increasing function, and if the value of y decreases as the value of x increases, then the function $y = F(x)$ is known as a decreasing function.
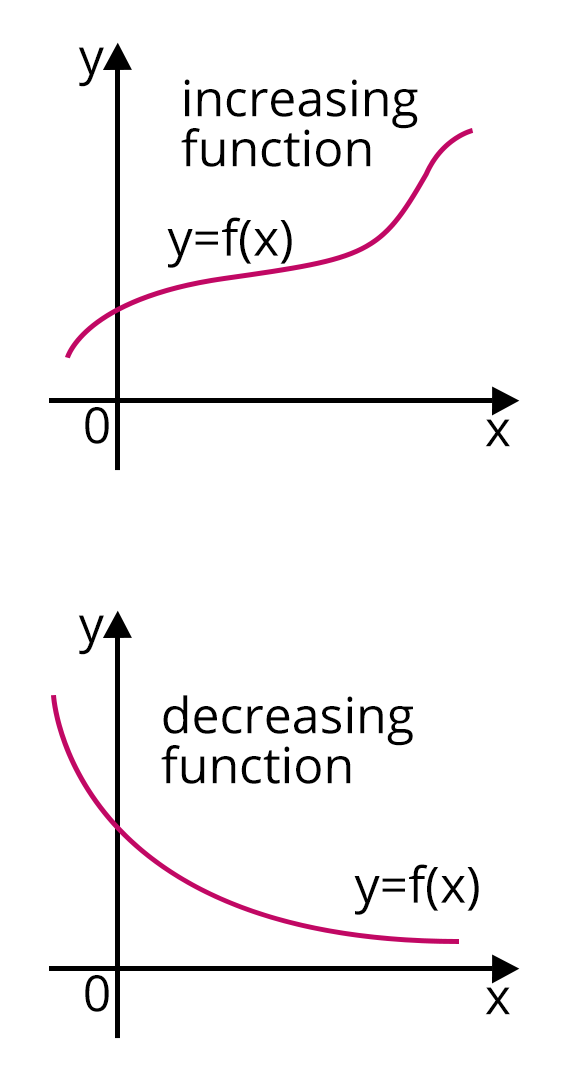
Increasing and Decreasing Function
3. Maxima and Minima of Functions
The extrema of a function are its maximum and minimum values. The maximum and minimum values of a function within a given set of ranges are known as maxima and minima. The maximum value of the function under the entire range is known as the absolute maxima, and the minimum value is known as the absolute minima.
In the diagram below, we get maximum values of the function at x = a and x = 0, and minimum values of the function at x = b and x = c. The maxima are all the peaks, and the minima are all the valleys.
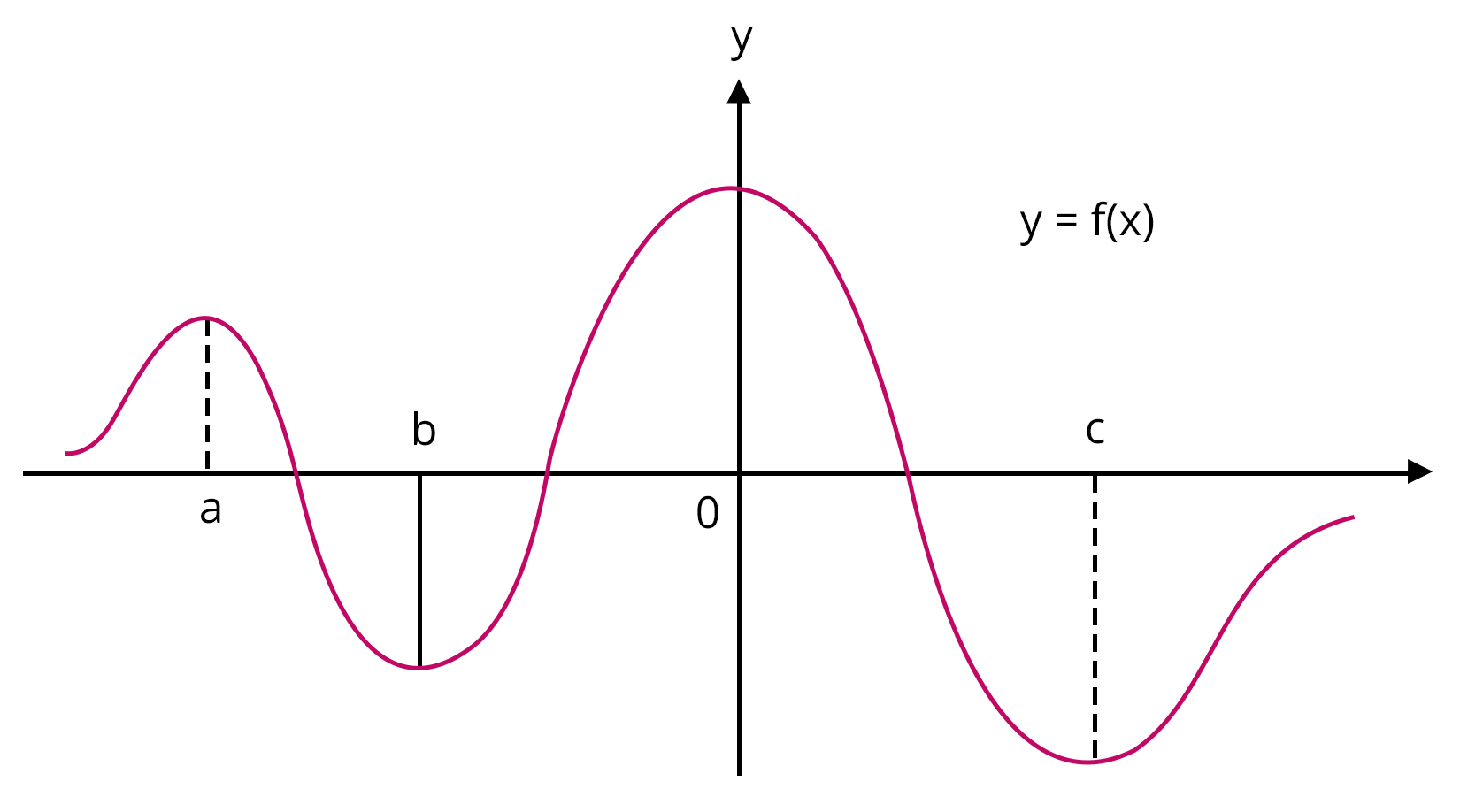
Maxima and Minima
4. Tangents and Normals
A tangent to a curve is a line that touches it at one point and has the same slope as the curve.
A line perpendicular to a tangent to the curve is called a normal to the curve.
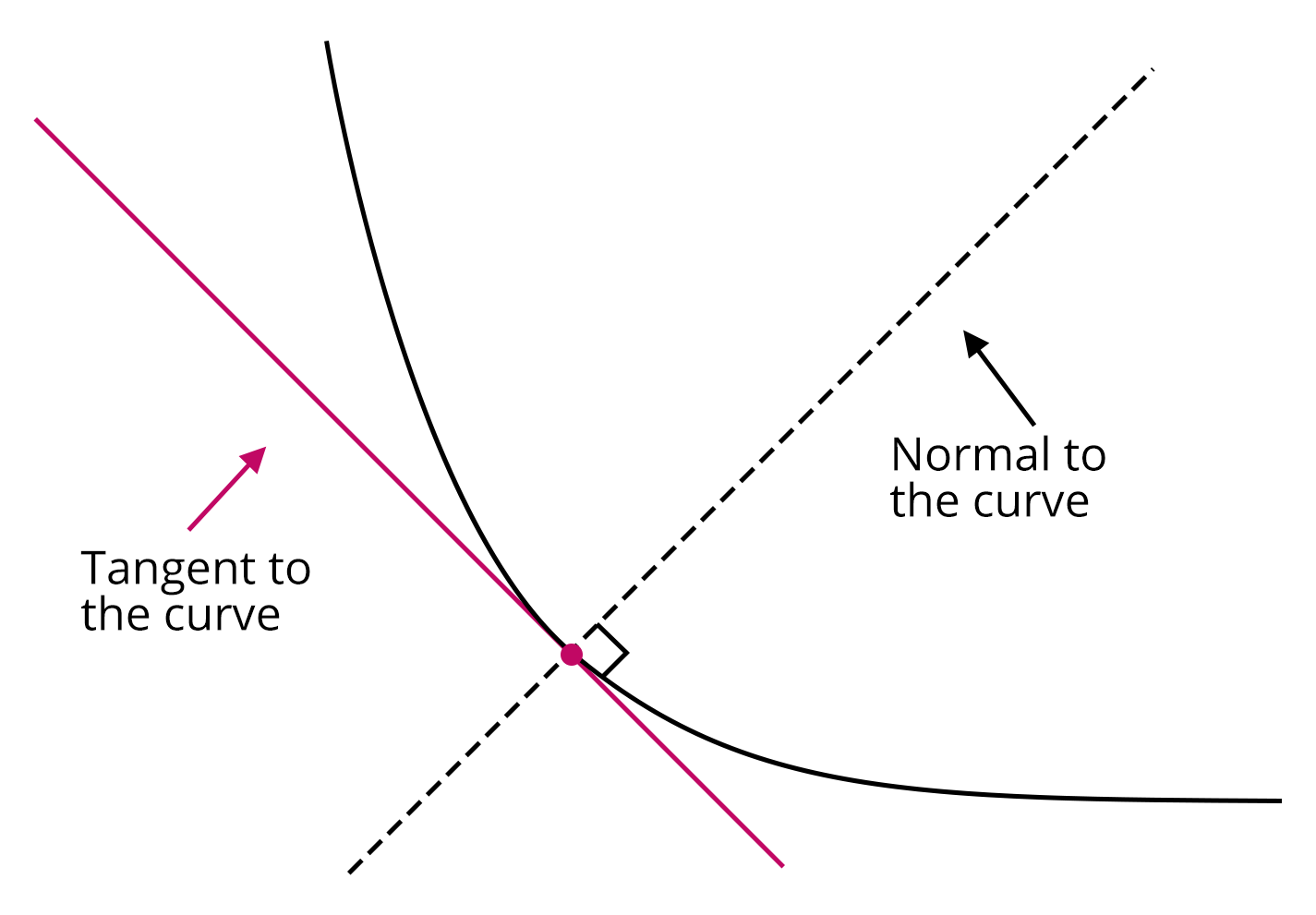
Tangent and Normal
Examples on Limit and Continuity
Example on Limit:
Evaluate $\underset{x\to 0}{\lim} \dfrac{x\cos{(x)}-\sin{(x)}}{x^2\sin{(x)}}$
Solution: Here the given limit is of the form $\dfrac{0}{0}$
Using L’Hospital Rule and differentiating, we get
$\Rightarrow \underset{x \to 0}{\lim} \dfrac{\cos{(x)}-x\sin{(x)}-\cos{(x)}}{x^2\cos{(x)} + 2x\sin{(x)}}$
$\Rightarrow \underset{x \to 0}{\lim} \dfrac{-\sin{(x)}}{x\cos{(x)} + 2\sin{(x)}}$
$\Rightarrow \underset{x \to 0}{\lim} \dfrac{\dfrac{-\sin{(x)}}{x}}{\cos{(x)} + \dfrac{2\sin{(x)}}{x}}$
$\Rightarrow \dfrac{-1}{1 + 2(1)}$
$\Rightarrow \dfrac{-1}{3}$
Example on Continuity:
Find the continuity of the function f(x) = 3x + 4 at the point x = 5.
Solution: The given function is f(x) = 3x + 4, and its value at the point x = 5 is f(5) = 19.
Let us find the limit of the function at the point x = 5.
$\underset{x \to 5}{\lim}f(x)$
$\Rightarrow \underset{x \to 5}{\lim} (3x + 4) $
$\Rightarrow 3(5) + 4 $
$\Rightarrow 15 + 4 = 19 = f(5)$
Therefore, the function f(x) is continuous at the point x = 5.
Previous Year’s Questions From JEE Main
1. If $f(1)=1, f^{\prime}(1)=2$ then $\underset{x \rightarrow 1}{\lim} \dfrac{\sqrt{f(x)}-1}{\sqrt{x}-1}$ is
Ans: Given function is $\underset{x \rightarrow 1}{\lim} \dfrac{\sqrt{f(x)}-1}{\sqrt{x}-1}$ and the limit is of the form (0/0)
Using L’Hospital's rule we get,
$\Rightarrow \underset{x \rightarrow 1}{\lim} \dfrac{\dfrac{1}{2 \sqrt{f(x)}} f^{\prime}(x)}{\dfrac{1}{2 \sqrt{x}}}$
$\Rightarrow \dfrac{f^{\prime}(1)}{\sqrt{f(1)}}$
As it is given that $f(1)=1, f^{\prime}(1)=2$
Hence $ \dfrac{f^{\prime}(1)}{\sqrt{f(1)}}=2$
2. $f(x)$ and $g(x)$ are two differentiable functions on $\left[0,2\right]$ such that $f^{\prime \prime}(x)-g^{\prime \prime}(x)=0$, $f^{\prime \prime}(1)=2 g^{\prime}(1)=4 f(2)=3 g(2)=9$ then $f(x)-g(x)$ at $x=3 / 2$ is
Ans: Given $f^{\prime \prime}(x)-g^{\prime \prime}(x)=0$
On Integrating the above equation we get,
$f^{\prime}(x)-g^{\prime}(x)=c$; $
$ \Rightarrow f^{\prime}(1)-g^{\prime}(1)=c$
$\Rightarrow 4-2 = c \Rightarrow c=2$
$\therefore f^{\prime}(x)-g^{\prime}(x)=2$
Again Integrating the above equation to reduce to f(x) and g(x) we get,
$f(x)-g(x)=2 x+c_{1}$
$\Rightarrow f(2)-g(2)=4+c_{1}$
$\Rightarrow 9-3=4+c_{1} ; \Rightarrow c_{1}=2$
$\therefore f(x)-g(x)=2 x+2$ at $x= \dfrac{3}{2}, f(x)-g(x)=3+2=5$.
3. Solve the limit $\underset{x \rightarrow \alpha}{\lim} \dfrac{1-\cos a(x-\alpha)(x-\beta)}{(x-\alpha)^{2}}$
Ans: Given, $\underset{x \rightarrow \alpha}{\lim} \dfrac{1-\cos a(x-\alpha)(x-\beta)}{(x-\alpha)^{2}}$
We know that $1-cos\theta = 2sin^2\theta$
Thus the given equation will become,
$\Rightarrow \lim _{x \rightarrow \alpha} \dfrac{2 \sin ^{2}\left(a \dfrac{(x-\alpha)(x-\beta)}{2}\right)}{(x-\alpha)^{2}}$
$\Rightarrow \lim _{x \rightarrow \alpha} \dfrac{2}{(x-\alpha)^{2}} \times \dfrac{\sin ^{2}\left(a\dfrac{(x-\alpha)(x-\beta)}{2}\right)} {\dfrac{a^{2}(x-\alpha)^{2}(x-\beta)^{2}}{4}}\times \dfrac{a^{2}(x-\alpha)^{2}(x-\beta)^{2}}{4}$
$\Rightarrow \dfrac{a^{2}(\alpha-\beta)^{2}}{2}$
4. Evaluate the following:
\[\lim_{x\rightarrow 0} \sqrt{2 + x} - \dfrac{\sqrt{2}}{x}\].
Solution: Substitute y = 2 + x so that when x0 , y 0. Then,
\[\lim_{x\rightarrow 0} \sqrt{2 + x} - \dfrac{\sqrt{2}}{x} = y\]
= \[\dfrac{y^{1/2} - 2^{1/2}}{y - 2}\]
= \[\dfrac{1}{2} (2)^{\dfrac{1}{2} - 1} = \dfrac{1}{2} (2)^{-\dfrac{1}{2}} = \dfrac{1}{2} \sqrt{2}\]
Practice Questions
1. Let $f(x)=4$ and $f^{\prime}(x)=4$. Then $\underset{x \rightarrow 2}{\lim} \dfrac{x f(2)-2 f(x)}{x-2}$ is given by
Ans: - 4
Hint: Apply L’Hospital rule
2. If $f(x+y)=f(x) . f(y) \forall x, y$ and $f(5)=2, f^{\prime}(0)=$ 3 then $f^{\prime}(5)$ is
Ans: 6
Hint: Differentiate with respect to x, treating y as constant
How Limits and Continuity Help to Score High in JEE Main Exam?
In the dynamic realm of the JEE Main exam, a mastery of foundational concepts such as Limits and Continuity is paramount. These concepts, denoted as \(\lim_{{x \to a}} f(x)\), serve as the bedrock of calculus, wielding significant influence over derivative and integral calculus applications. A nuanced understanding of Limits and Continuity is indispensable for candidates aiming to excel in this challenging examination.
Key Concepts:
$\textbf{Limits Exploration:}$ Understanding the behavior of a function as it approaches a specific point \(a\) is encapsulated in the concept of limits.
Strategic Techniques: Proficiency in techniques like L'Hôpital's Rule is crucial for navigating indeterminate forms and solving complex problems.
Continuity Foundations: Continuity, an extension of Limits, ensures a seamless and defined function behavior at specific points.
Calculus Pillars: Limits and Continuity form the foundational pillars of calculus, influencing derivative and integral calculus applications.
Scoring High in JEE Main:
Strategic Application: Applying Limits and Continuity principles strategically is essential for solving complex calculus-related problems.
Scenario Handling: Proficiency in discerning and handling scenarios involving piecewise or composite functions is crucial for success.
Overall Mathematical Proficiency: A robust foundation in Limits and Continuity not only ensures success in calculus questions but also primes candidates for broader mathematical applications.
JEE Main Maths - Limits, Continuity and Differentiability Study Materials
Here, you'll find a comprehensive collection of study resources for Limits, Continuity and Differentiability designed to help you excel in your JEE Main preparation. These materials cover various topics, providing you with a range of valuable content to support your studies. Simply click on the links below to access the study materials of Limits, Continuity and Differentiability and enhance your preparation for this challenging exam.
JEE Main Maths Study and Practice Materials
Explore an array of resources in the JEE Main Maths Study and Practice Materials section. Our practice materials offer a wide variety of questions, comprehensive solutions, and a realistic test experience to elevate your preparation for the JEE Main exam. These tools are indispensable for self-assessment, boosting confidence, and refining problem-solving abilities, guaranteeing your readiness for the test. Explore the links below to enrich your Maths preparation.
Conclusion
Some of the important concepts covered in this chapter include limits, functions, differentiability, continuity, and L’Hospital Rule. It is one of the important chapters in class 12 and it can be continued in higher classes also. Many questions will be asked from this chapter in JEE Main and JEE Advanced both. So the students preparing for JEE must practice the questions from this chapter.
The chapter on "Limits, Continuity, and Differentiability" is a fundamental cornerstone in the journey of JEE Main aspirants. It lays the groundwork for understanding the core concepts of calculus, which are pivotal not only for success in the exam but also for advanced studies in mathematics and its applications in various fields. Mastering limits, continuity, and differentiability is essential for solving complex problems in physics, engineering, and beyond. The knowledge gained in this chapter equips students with the ability to analyze functions, approximate values, and make accurate predictions, fostering a deeper appreciation of mathematics in practical contexts.












FAQs on JEE Main Important Chapter - Limits, Continuity and Differentiability
1. Mention the most important differentiation of the functions f(x) based on the type of functions.
Some of the most important differentiation of the functions f(x) based on the type of functions are given below:
Derivative of Composite Function
Derivatives of Implicit Functions
Derivatives of Inverse Trigonometric Functions
Derivatives of Exponential Functions
Derivatives of Logarithmic Functions
Derivatives of Functions in Parametric Forms
2. What Are the Applications of Calculus Limits in Real Life?
Limits are also utilized in practice to approximate the calculation of derivatives. Engineers will estimate a function using small changes in the function and then try to determine the derivative of the function using smaller spacing in the function following sample intervals in order to do computations.
3. Mention two of the most important theorems on continuity and differentiability
Rolle's Theorem - If a function f(x) is continuous across the interval $\left[a, b\right]$ and differentiable across the interval (a, b), such that f(a) = f(b), and a, b are some real numbers. Then there exists a point c in the interval $\left[a, b\right]$ such that $f^\prime(c) = 0$.
Mean Value Theorem - If a function f(x) is continuous across the interval $\left[a, b\right]$ and differentiable across the interval (a, b), then there exists a point c in the interval $\left[a, b\right]$ such that $f^\prime(c) = \dfrac{f(b) - f(a)}{b - a}$.



