




How Does Fluid Pressure Work in Real Life? Examples and Applications
Fluid pressure is a fundamental concept in physics that describes the force exerted by a fluid per unit area at any given point within the fluid or on the surface of objects in contact with the fluid. Understanding fluid pressure is essential for solving problems in fluid mechanics, which is a key topic for JEE preparation.
Definition of Fluid Pressure
Fluid pressure refers to the normal force exerted by a fluid on a surface per unit area. The pressure at a point in a fluid at rest is the same in all directions and always acts perpendicular to the containing surface.
Mathematical Expression for Fluid Pressure
The basic formula for pressure is the ratio of force to area, expressed as
$P = \dfrac{F}{A}$
For fluids, the pressure at a depth $h$ from the surface is given by
$P = P_0 + \rho g h$
where $P_0$ is the reference (atmospheric) pressure, $\rho$ is the fluid density, $g$ is the acceleration due to gravity, and $h$ is the depth below the surface.
Further explanation of pressure and hydrostatics can be found at Fluid Pressure.
Units and Measurement of Fluid Pressure
The SI unit of pressure is the Pascal (Pa), equivalent to $1~\mathrm{N/m^2}$. Fluid pressure is measured using instruments such as barometers and manometers.
Comparative analysis of pressure measurement devices is available at Barometer and Manometer.
Factors Affecting Fluid Pressure
Several factors influence fluid pressure at a point within a static fluid:
- Density of the fluid ($\rho$)
- Depth below the fluid surface ($h$)
- Acceleration due to gravity ($g$)
- Presence of any additional external pressure
Variation of Fluid Pressure with Depth
Fluid pressure increases with an increase in depth. This relationship is linear for an incompressible fluid and is governed by the equation $P = P_0 + \rho g h$.
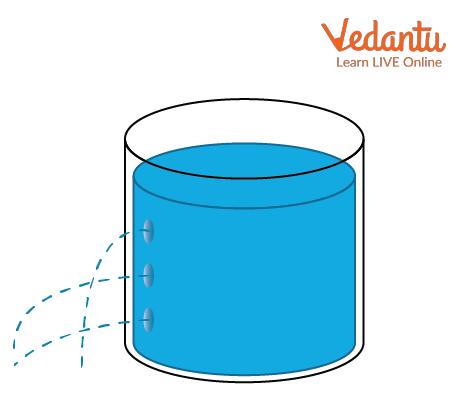
The diagram above illustrates that pressure is minimal at the top surface and maximal at the bottom for a container filled with liquid.
Direction of Fluid Pressure
At a given depth, the pressure exerted by the fluid is isotropic, meaning it acts equally in all directions. This property ensures that objects at the same depth in a fluid experience the same pressure, regardless of orientation.

Pascal's Law
Pascal’s Law states that the pressure applied to any part of a confined, incompressible fluid is transmitted equally, undiminished, in all directions throughout the fluid. This principle forms the basis for devices like hydraulic lifts and presses.
Types of Fluid Pressure
Fluid pressure is typically classified as:
- Static pressure: Pressure in a stationary fluid
- Dynamic pressure: Pressure due to fluid motion
Properties and Characteristics of Fluid Pressure
- Pressure increases with depth for static fluids
- It is independent of container shape
- Pressure at equal depth is same in all directions
- Acts perpendicular to any surface in the fluid
Fluid Density and Its Role
The density of a fluid ($\rho$) is defined as mass per unit volume: $\rho = \dfrac{m}{V}$. Higher density leads to a greater pressure at a given depth.
Solved Examples in Fluid Pressure
Application of fluid pressure concepts is essential for solving numerical problems in exams. Typical questions require substituting known values into standard formulas.
| Example | Solution Steps |
|---|---|
| Calculate pressure 14 m below water surface ($\rho = 1.03 \times 10^3~\mathrm{kg/m^3}$, $g = 9.8~\mathrm{m/s^2}$, $P_0 = 1.01 \times 10^5~\mathrm{Pa}$) | $P = 1.01 \times 10^5 + 1.03 \times 10^3 \times 9.8 \times 14 = 2.42 \times 10^5~\mathrm{Pa}$ |
| Find force on area $A = 6 \times 10^{-4}~\mathrm{m^2}$ at $h = 0.85~\mathrm{m}$ in water ($\rho = 1000~\mathrm{kg/m^3}$, $g = 10~\mathrm{m/s^2}$) | $F = \rho g h A = 1000 \times 10 \times 0.85 \times 6 \times 10^{-4} = 5.1~\mathrm{N}$ |
Centre of Pressure
The centre of pressure is the point on a submerged surface at which the resultant pressure force acts. Its position depends on the orientation and shape of the surface and is essential for stability analysis in fluid statics.
Applications in Everyday Physics
Fluid pressure concepts are applied in hydraulic machinery, fluid gauges, aircraft design, and medical devices. Devices such as the fluid pressure gauge and fluid pressure sensor rely on these principles for accurate measurements.
Related Topics in Fluid Mechanics
Deeper topics include hinge force calculations (Hinge Force) and the study of upthrust and buoyancy (Upthrust and Law of Floatation), which are directly related to fluid statics and fluid pressure.
FAQs on Understanding Fluid Pressure: Concepts, Formula, and Uses
1. What is fluid pressure?
Fluid pressure is the force exerted by a fluid per unit area on any surface within the fluid. It acts in all directions and increases with depth in a liquid.
Key points:
- Measured in Pascals (Pa), also known as N/m²
- Depends on density of the fluid, acceleration due to gravity, and depth
- Formula: P = hρg, where P is pressure, h is height (depth), ρ is density, and g is gravity
2. How is pressure in liquids calculated?
Pressure in liquids is calculated using the formula P = hρg, where pressure is directly proportional to depth, density of the liquid, and gravitational acceleration.
Steps:
- Measure the depth (h) of the liquid column
- Find the density (ρ) of the liquid
- Use standard gravity (g = 9.8 m/s²)
- Multiply: P = h × ρ × g
3. Why does fluid pressure increase with depth?
Fluid pressure increases with depth because the weight of the liquid above adds more force on lower layers.
- Deeper layers support the weight of the fluid above
- Hydrostatic pressure increases as you go deeper
- This effect is described by P = hρg
4. What are some real-life examples of fluid pressure?
Fluid pressure is observed in many everyday situations.
- Water supply systems use pressure to move water up buildings
- When swimming or diving, you feel more pressure as you go deeper
- Hydraulic brakes in vehicles work using liquid pressure
- Atmospheric pressure pushing mercury up a barometer tube
5. How does atmospheric pressure compare to fluid pressure in liquids?
Atmospheric pressure is the force exerted by the air around us, while fluid pressure in liquids comes from the weight of the liquid column.
- Both measured in Pascals (Pa)
- Atmospheric pressure at sea level is about 1 × 105 Pa
- Liquid pressure depends on depth and density, atmospheric pressure depends on altitude
6. State the formula for pressure at a point in a liquid and name the quantities involved.
The formula for pressure at a point in a liquid is P = hρg.
- P = Pressure (in Pascals, Pa)
- h = Vertical depth of the point from the free surface (in meters)
- ρ = Density of the liquid (kg/m³)
- g = Acceleration due to gravity (9.8 m/s²)
7. Why do dams have thicker walls at the bottom?
Dams have thicker walls at the bottom because fluid pressure is greater at greater depths, so more strength is needed to withstand the increased pressure.
- Pressure depends on depth (P = hρg)
- More water above means more force exerted at the base
8. What factors affect the pressure exerted by a liquid?
The pressure exerted by a liquid depends on:
- Depth of the fluid (h)
- Density of the liquid (ρ)
- Acceleration due to gravity (g)
9. What is the SI unit of pressure?
The SI unit of pressure is the Pascal (Pa), which is equal to one Newton per square meter (N/m²).
10. What do you mean by pressure is exerted equally in all directions in a liquid?
Pressure in a liquid is exerted equally in all directions, meaning at a given depth, pressure acts the same horizontally and vertically.
- This property allows hydraulic machines to function
- Known as Pascal's Law

































