Perimeter and Area Class 7 important questions with answers PDF download
FAQs on CBSE Important Questions for Class 7 Maths Perimeter and Area - 2025-26
1. How can I benefit from practising Maths Important Questions?
The examination pattern is divided into four sections- Section A, B, C, and D. To solve questions from each section you need to practise a lot of questions regularly. Practising important questions will make you familiar with the type of questions. If you are well versed with the concepts you will be easily able to solve direct questions.
To solve word problems you will need to convert them into solvable equations first before you attempt them. Practising important questions will give you the confidence to solve any difficult question that comes in the examination.
One great way to practise important questions from each chapter is to solve sample papers. If you solve sample papers under the stipulated time it will benefit you because you will be familiar with working under time pressure. Focus on understanding the concept of the important questions and the pattern they follow.
2. What is the difference between perimeter and area?
The perimeter of a closed figure is the distance around it, whereas its area is the fraction of a plane or region it encloses. A regular polygon's perimeter is equal to the number of sides multiplied by the length of one side. Similarly, the perimeter and area of various forms vary and are calculated using different formulae based on this concept. Perimeter and area are important concepts of maths and have significant weightage in the exam. You can prepare them well with Vedantu.
3. How can I download the PDF file for the Solutions of NCERT Class 7 Maths Chapter 9?
The solutions are easily available on the Vedantu site.
Click on this link
The webpage with Vedantu’s solutions for Class 7 Maths
Chapter 9 will open.
To download this, click on the Download PDF button and you can view the solutions offline.
The Vedantu website has a variety of instructors that can aid you with this or any other chapter.
4. What is an irregular shape Class 7?
Any size and length is a possibility for an irregular form. A kite, a diamond shape, a leaf, and other irregular forms may be seen all around us. An irregular form is defined as one whose sides and angles are not of equal length. Rocks, prisms, beans, and screws are examples of irregular solids. Each of these things has a unique irregular form that isn't made up of regular shapes. The difficulty to estimate an irregular solid area, volume, or mass by measuring its length, breadth, and height distinguishes it.
5. What is the difference between irregular and regular shapes?
An irregular form can be any size and length, whereas a regular shape has equal sides and angles. Thus, the area of a regular shape may be calculated directly using appropriate formulae, but the area of an irregular shape can be calculated by decomposing an irregular shape into numerous regular ones. Irregular shapes’ areas are generally harder to calculate due to their unpredictability. Hence, an approach different from the norm, while calculating the area of regular shapes, has to be taken for irregular shapes.
6. How do you find areas of irregular shapes?
To calculate the area of an irregular form, first split it into regular shapes that you can identify, such as triangles, rectangles, circles, squares, and so on. Then, to create an area of irregular forms, determine the area of each individual shape and put them together. Due to their unpredictability, the areas of irregular forms are typically more difficult to compute. For more problems regarding this, you can visit the Vedantu site.
7. How does knowing perimeter and area help in real life?
Perimeter and area are useful for things like measuring land, building walls, painting surfaces, and even in designing spaces like gardens and rooms.
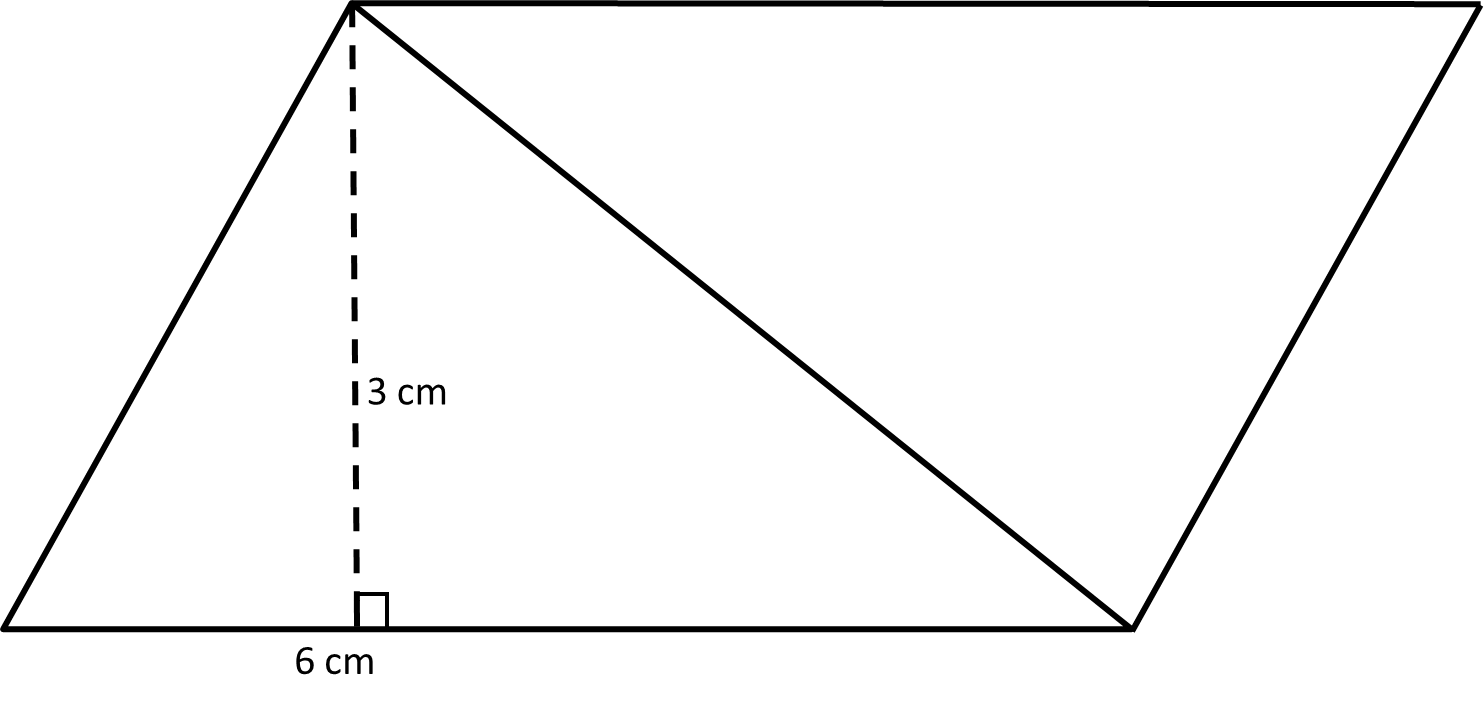
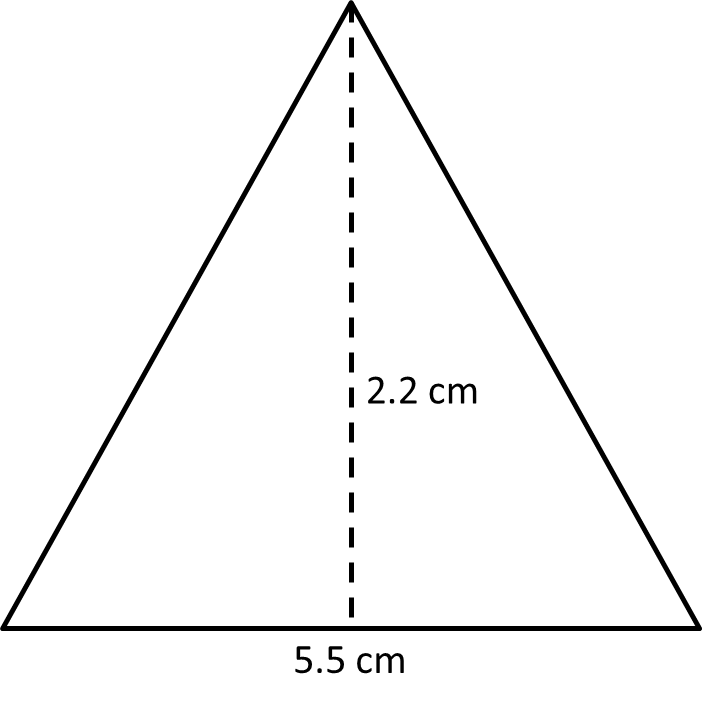
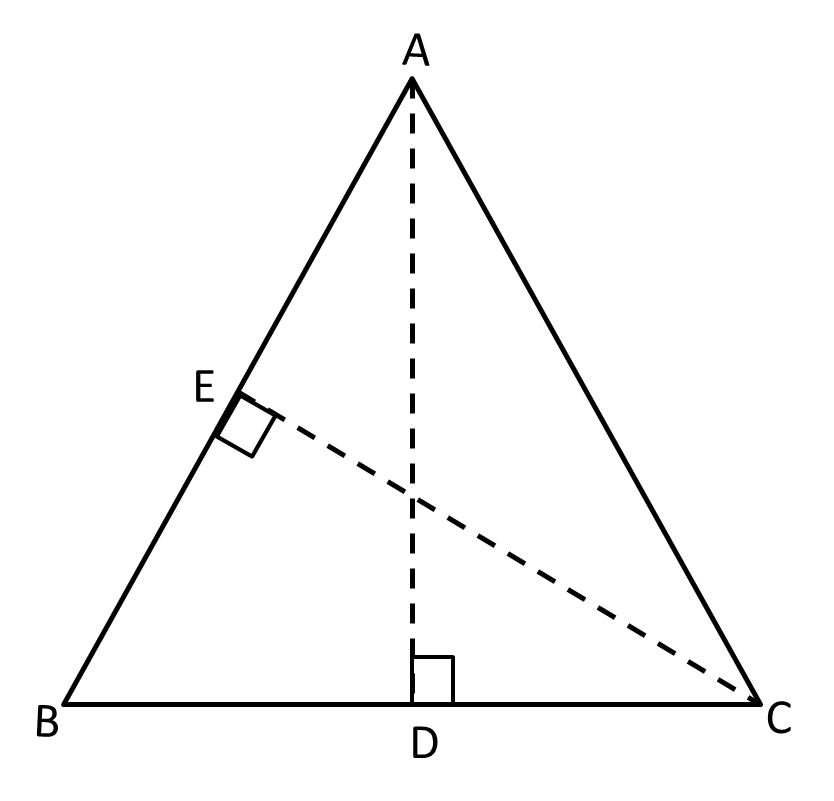
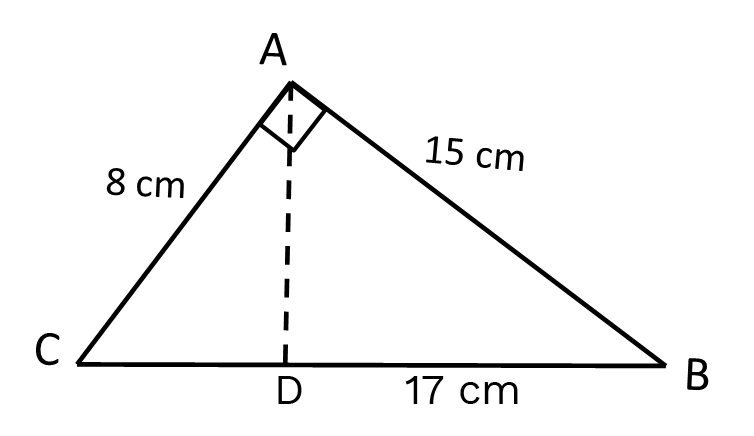
8. What is the formula for finding the area of a triangle?
The area of a triangle is calculated using the formula $\dfrac{1}{2} \times \text{Base} \times \text{Height}$.
9. Why is it important to learn different formulas for area and perimeter?
Each shape has a unique formula for perimeter and area. Learning these helps you solve problems related to different shapes accurately.
10. How can I remember all the formulas for perimeter and area?
Regular practice and using the formulas in solving questions will help you remember them. Writing them down and revising them frequently also helps.
11. How can practising perimeter and area questions improve my maths skills?
Practising these questions improves calculation skills, problem-solving ability, and helps you understand geometric measurements, which are useful in many real-life situations.