NCERT Exemplar for Class 9 Maths Chapter 4 - Linear Equations in Two Variables (Book Solutions)

Sample Questions

1. The linear equation \[3x-y = x - 1\] has:

(A) A unique solution

(B) Two solutions

(C) Infinitely many solutions

(D) No solution

Ans: Option (C) is the correct answer.

The linear equation \[3x - y = x- 1\]

On rearranging the terms, we get:

$y = 2x + 1$ , 

To find the value of y, select the random value of the variable x.

Hence, the system of linear equations \[3x-y = x - 1\] will have infinitely many solutions.

2. A linear equation in two variables is of the form \[ax + by\; + \,c  = \,0,\] where

(A) \[a \ne 0, b \ne 0\]  

(B) \[a = 0, b \ne 0\]

(C) \[a \ne 0, b = 0\]

(D) \[a = 0, c = 0\] 

Ans: Option (A) is the correct answer.

An equation of the form \[ax + by\; + \,c{\text{ }} = \,0,\] where $a$ ,$b$ and $c$  are real numbers such that \[a \ne 0,{\text{ }}b \ne 0\], is called a linear equation in two variables.

If any of these $a\;{\text{or}}\;b$ is zero i.e. \[a \ne 0,{\text{ }}b = 0\]  then the linear equation is said to be in one variable \[ax + \,c{\text{ }} = \,0\].

3. Any point on the \[y - \] axis is of the form

(A) \[\left( {x, 0} \right)\]
(B) \[\left( {x, y} \right)\]
(C)\[\left( {0, y} \right)\]
(D) \[\left( { y, y} \right)\] 

Ans: Option (C) is the correct answer.

The point on the \[y - \] axis.

On y-axis, x-coordinate = abscissa is zero and y-coordinate is any real number. 

So, any point on the \[y - \] axis is of the form\[\left( {0,{\text{ }}y} \right)\].

Exercise 4.1

1. The linear equation \[2x-5y = 7\] has

(A) A unique solution                                

(B) Two solutions 

(C) Infinitely many solutions                     

(D) No solution

Ans: Option (C) is the correct answer.

The linear equation is \[2x-5y = 7\]

On rearranging the terms, we get:

$\Rightarrow 2x = 7 + 5y$

$\Rightarrow y = \dfrac{{2x - 7}}{5}$ 

To find the value of y, select the random variable x.

The linear equation \[2x-5y = 7\] has infinitely many solutions.

2. The equation \[2x + 5y = 7\] has a unique solution, if \[x, y\] are:

(A) Natural numbers                                   

(B) Positive real numbers

(C) Real numbers                                         

(D) Rational numbers

Ans: Option (A) is the correct answer.

There is only one unique solution which satisfies the given linear equation \[2x + 5y = 7\]i.e.$\left(1, 1 \right)$ which comes in the category of natural numbers. On the other hand positive real numbers, real numbers, and rational numbers have many pairs which will satisfy the given linear equation.

3. If \[\left( {2\;, 0} \right)\] is a solution of the linear equation \[2x + 3y = \;k,\] then the value of \[k\] is 

(A) 4

(B) 6 

(C) 5

(D) 2

Ans: Option (A) is the correct answer.

Let \[\left({2, 0} \right)\] is a solution of the linear equation \[2x + 3y = \;k\].

Hence, the given solution satisfies the linear equation.

Substituting the values $x\; = \;2$ and $y\; = \,0$ in \[2x + 3y = \;k,\]

$2x + 3y = k$

$\Rightarrow 2(2) + 3(0) = k$

$\Rightarrow \;k = 4$ 

Hence, the value of k is 4.

4. Any solution of the linear equation \[2x + 0y + 9 = 0\] in two variables is of the form

(A) \[\left( {- \dfrac{9}{2} , m} \right)\]

(B) \[\left( {n\;,\;- \dfrac{9}{2} } \right)\]

(C) \[\left( {0\;,\;- \dfrac{9}{2} } \right)\]

(D) \[\left( { - 9\;,0\;} \right)\] 

Ans: Option (A) is the correct answer.

The linear equation \[2x + 0y + 9 = 0\] has the coefficient of $y$ as zero, this vanishes the $y$ term.

So, \[2x+  9= 0\] 

$\Rightarrow x =  - \dfrac{9}{2}$ 

The coordinates $(x,\;y)$ are \[\left( -\dfrac{9}{2}, m \right)\], assuming the value of $y$ be $m\;.$

5. The graph of the linear equation \[2x  +  3y  =  6\] cuts the \[y - \] axis at the point

(A) \[\left( {2, 0} \right)\]

(B) \[\left( {0, 3} \right)\] 

(C) \[\left( {3, 0} \right)\]

(D) \[\left( {0, 2} \right)\] 

Ans: Option (D) is the correct answer.

The graph of the linear equation \[2x + 3y =6 \] cuts the \[y - \] axis i.e. the $x-$ coordinate will be zero. 

So, substituting $x\; = \;0$ in \[2x + 3y = 6\], we get, 

$2\times 0 + 3y = 6$

$\Rightarrow 3y = 6$

$\Rightarrow y = 2$ 

Therefore, the graph of the linear equation \[2x +3y = 6\] cuts the \[y - \] axis at the point \[\left( 0, 2 \right)\]

6. The equation \[x  =  7,\] in two variables, can be written as 

(A) \[1 . x  +  1 . y  =  7\] 

(B) \[1. x  +  0. y  =  7\;\]    

(C) \[0 . x  +  1 . y  =  7\;\;\] 

(D) \[0 . x  +  0 . y  =  7\] 

Ans: Option (B) is the correct answer.

The equation \[x{\text{  =  7}},\] 

Substituting the value \[x{\text{  =  7}},\] in every option,

${\text{ }}x{\text{ }} + {\text{ }}0.{\text{ }}y{\text{ }} = {\text{ }}7\;$

$\Rightarrow 1\left( 7 \right) + 0 = 7$

$\Rightarrow 7 = 7$

${\text{L}}{\text{.H}}{\text{.S}} = {\text{R}}{\text{.H}}{\text{.S}}$ 

7. Any point on the \[x - \] axis is of the form 

(A) \[\left( {x, y} \right)\;\] 

(B) \[\left( {0, y} \right)\;\]  

(C) \[\left( {x, 0} \right)\;\] 

(D) \[\left( {x, x} \right)\]

Ans: Option (C) is the correct answer.

If the point is located on the \[x - \] axis then its $y -$ coordinate is equal to zero. 

$\Rightarrow y\; = \;{\text{0}}$

So, any point on the \[x - \] axis is of the form \[\left( {x,{\text{ }}0} \right)\;\;.\]

8. Any point on the line \[y = x\] is of the form

(A)\[\left( {a, a} \right)\] 

(B) \[\left( {0, a} \right)\]  

(C)\[\left( {a, 0} \right)\] 

(D) \[\left( {a,\,- a} \right)\] 

Ans: Option (A) is the correct answer.

On \[y = x\], $y-$ coordinate = $x -$ coordinate. 

The point is located on \[y = x\] 

$y- $coordinate =$x-$ coordinate. 

\[(x,y) = \left( {a,{\text{ }}a} \right)\]

Hence, any point on the line \[y = x\] is of the form \[\left( {a,{\text{ }}a} \right)\]

9. The equation of \[x - \]axis is of the form

(A) \[x = 0\]  

(B) \[y = 0\]    

(C) \[x + y = 0\] 

(D) \[x = y\] 

Ans: Option (B) is the correct answer.

On the x-axis, the coordination of any point is of the type (a, 0), a is any real number.

This means that value of $y\; - \;$ coordinate will be zero $\left( {y\; = \;{\text{0}}} \right)\;.$

So, the equation of the \[x - \] axis is of the form \[y = 0\].

10. The graph of \[y = 6\] is a line

(A) Parallel to \[x - \]axis at a distance 6 units from the origin.

(B) Parallel to \[y - \]axis at a distance 6 units from the origin.

(C) Making an intercept 6 on the \[x - \] axis.

(D) Making an intercept 6 on both the axes.

Ans: Option (A) is the correct answer.

Plot the graph of \[y = 6\], by choosing the random values of x,

Choose 

x = 1,y = 6 $\Rightarrow (x,y) = (1,6)$

x = 5,y = 6 $\Rightarrow (x,y) = (5,6)$

x =  - 3,y = 6 $\Rightarrow (x,y) = ( - 3,6)$ 

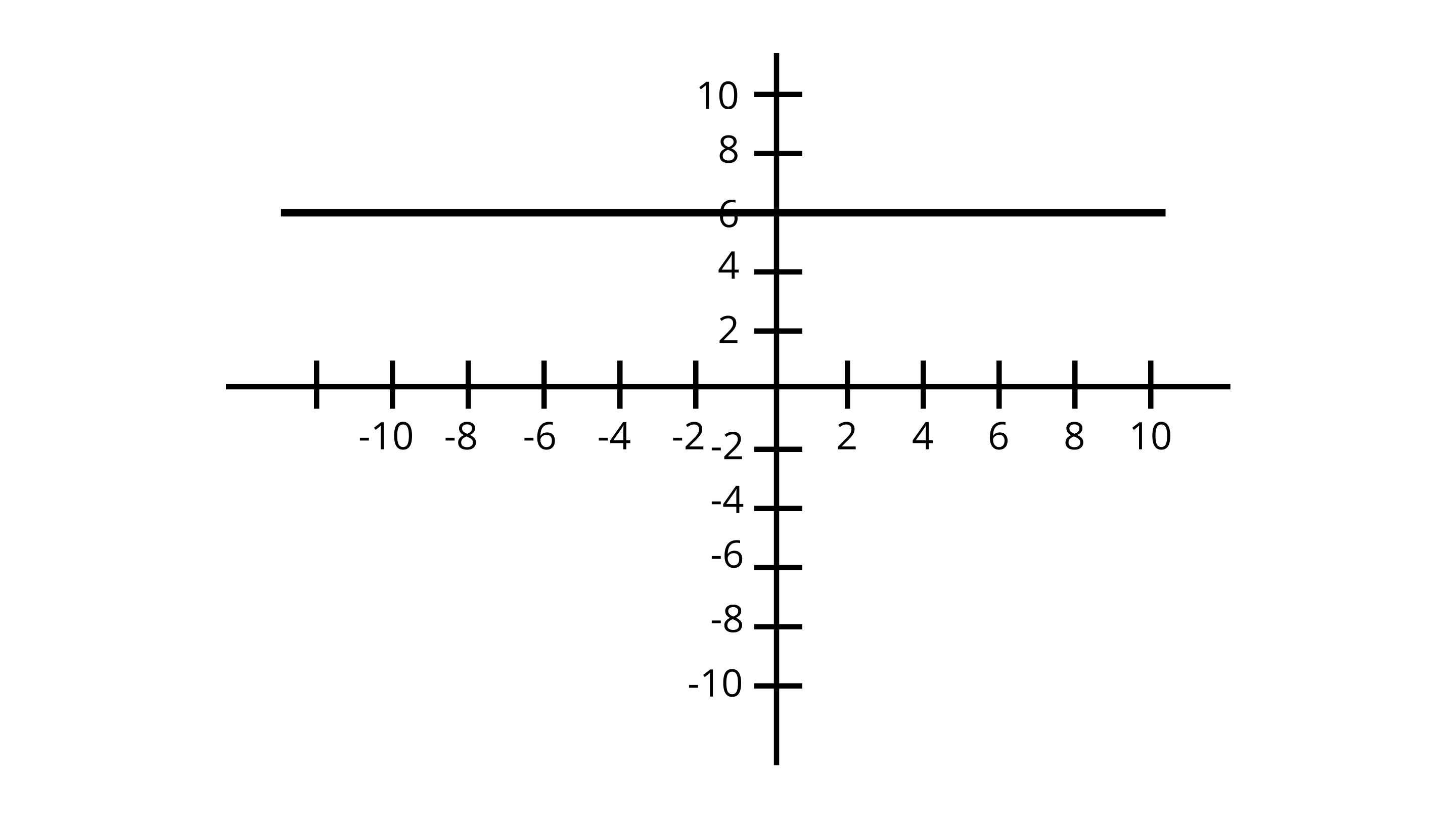
From the graph, we can say that

The graph of \[y = 6\] is a line Parallel to \[x - \] axis at a distance 6 units from the origin.

11. \[x = 5, y = 2\] is a solution of the linear equation

(A) \[x + 2 y = 7\]

(B) \[5x + 2y = 7\] 

(C) \[x + y = 7\] 

(D) \[5 x + y = 7\] 

Ans: Option (C) is the correct answer.

A solution of a linear equation is the values to the variables for which the equation is satisfied.

On analyzing the given linear equations we found that \[x = 5,{\text{ }}y = 2\] is a solution of \[x + y = 7\]. 

${\text{L}}{\text{.H}}{\text{.S}}$

$\Rightarrow x + y = 5 + 2 = 7$

$= RHS$ 

Hence, \[x = 5,{\text{ }}y = 2\] is a solution of the linear equation of \[x + y = 7\].

12. If a linear equation has solutions \[\left( {-2, 2} \right), \left( {0, 0} \right) \text{ and } \left( {2, - 2} \right),\]  then it is of the form 

(A) \[y-x = 0\]  

(B) \[x + y = 0\] 

(C) \[-\;2x + y = 0\;\;\]

(D) \[-\;x + 2y = 0\] 

Ans: Option (B) is the correct answer.

A solution of a linear equation is the values to the variables for which the equation is satisfied.

On analyzing the linear equations in the options we found that,

If a linear equation has solutions \[\left( {-2,{\text{ }}2} \right),{\text{ }}\left( {0,{\text{ }}0} \right){\text{ and }}\left( {2,{\text{ }}-{\text{ }}2} \right),\]  then it is of the from \[x + y = 0\].

13. The positive solutions of the equation \[ax + by + c = 0\] always lie in the 

(A) 1st quadrant

(B) 2nd quadrant 

(C) 3rd quadrant 

(D) 4th quadrant

Ans: Option (A) is the correct answer.

We know that: 

The signs of the coordinates of a point in the XY- plane.

From the above table, we can conclude that 

The positive solutions of the equation \[ax + by + c = 0\] always lie in the Quadrant I.

14. The graph of the linear equation \[2x + 3y =  6\] is a line which meets the \[x - \] axis at the point- 

(A)\[\left( {0,{\text{ }}2} \right)\] 

(B)\[\;\left( {2,{\text{ }}0} \right)\] 

(C)\[\;\left( {3,{\text{ }}0} \right)\]

(D)\[\;\left( {0,{\text{ }}3} \right)\] 

Ans: Option (C) is the correct answer.

The graph of the linear equation \[2x + 3y = {\text{ }}6\] is a line which meets the \[x - \] axis.

On \[x - \] axis, y-coordinate = 0

To find x-coordinate, substitute the value of $y$ in the given linear equation.

$2x + 3y = {\text{ }}6$

$\Rightarrow 2x\; + \;3(0)\; = \;6$

$\Rightarrow x\; = \;\dfrac{6}{2}\; = \;3$ 

Hence, the graph of the linear equation \[2x + 3y = {\text{ }}6\] is a line which meets the \[x - \] axis at the point- \[\;\left( {3,{\text{ }}0} \right)\].

15. The graph of the linear equation \[y = x\] passes through the point 

(A)\[\left( {\dfrac{3}{2},  - \;\dfrac{3}{2}} \right)\]

(B)\[\;\left( {0, \;\dfrac{3}{2}} \right)\]   

(C)\[\;\left( {1, 1} \right)\] 

(D)\[\left( { - \;\dfrac{1}{2}\;,\;\dfrac{1}{2}} \right)\]

Ans: Option (C) is the correct answer.

The linear equation \[y = x\].

For \[y = x\], we have:

x - coordinate = y – coordinate.

Hence, from the given options the graph of the linear equation \[y = x\] passes through the point\[\;\left( 1, 1 \right)\].

16. If we multiply or divide both sides of a linear equation with a non-zero number, then the solution of the linear equation:

(A) Changes 

(B) Remains the same 

(C) Changes in case of multiplication only

(D) Changes in case of division only

Ans: Option (B) is the correct answer.

The mathematical property states that if any linear equation is multiplied or divided both sides by a non-zero number then the solutions of that equation remain the same i.e. no changes are observed.

17. How many linear equations in $x$ and \[y\] can be satisfied by \[x = 1 \;\text{ and } y = 2\] ? 

(A) Only one

(B) Two

(C) Infinitely many 

(D) Three

Ans: Option (C) is the correct answer.

Assume the linear equation $ax\; + \;by\; + c\; = \;0$ and substituting the values \[x{\text{ }} = {\text{ }}1{\text{ }}\;{\text{and }}\;y{\text{ }} = {\text{ }}2\], $a\; + 2b\; + \;c\; = \;0$ is obtained where $a\;,\;b\;\& \;c$ are real numbers. The different values of $a\;,\;b\;\& \;c$ satisfies $a\; + 2b\; + \;c\; = \;0$ so it has infinitely many solutions.

18. The point of the form \[\left( {a, a} \right)\] always lies on: 

(A) $x -$ axis

(B) $y -$ axis

(C) On the line \[y = x\]

(D) On the line \[x  +  y  =  0\] 

Ans: Option (C) is the correct answer.

The given point is \[\left( {a,{\text{ }}a} \right)\].

\[\Rightarrow x - {\text{coordinate }} = {\text{ }}y - {\text{coordinate}}\]

We know that: 

For the line \[y = x\],

\[\Rightarrow x - {\text{coordinate }} = {\text{ }}y - {\text{coordinate}}\]

Hence, the point of the form \[\left( {a,{\text{ }}a} \right)\]  always lies on the line \[y = x\].

19. The point of the form \[\left( {a,- a} \right)\] always lies on the line

(A) \[x = a\] 

(B) \[y = - a\]

(C) \[y = x\]

(D) \[x + y = 0\] 

Ans: Option (D) is the correct answer.

The given point is\[\left( {a,-{\text{ }}a} \right)\].

Here, the coordinates are opposite in signs.

We know that:

For the line \[x + y = 0\], 

\[\Rightarrow x =  - y\]

\[\Rightarrow x-{\text{coordinate }} = - y-{\text{coordinate}}\]

\[\Rightarrow \] The coordinates are opposite in signs.

The point of the form \[\left( {a,-{\text{ }}a} \right)\] always lies on the line \[x + y = 0\].

Sample Questions

1. Write whether the following statements are True or False? Justify your answers. 

(i). \[ax + by + c = 0,\] where \[a, b \text{ and } c\] are real numbers, is a linear equation in two variables. 

Ans: The given statement is “\[ax + by + c = 0,\] where \[a,{\text{ }}b{\text{ and }}c\] are real numbers, is a linear equation in two variables.”

We know that:

An equation of the form \[ax + by\; + \,c  = \,0,\] where $a$ ,$b$ and $c$  are real numbers such that \[a \ne 0, b \ne 0\], is called a linear equation in two variables. 

Hence, the given statement is false.

(ii). A linear equation \[2x + 3y = 5\] has a unique solution.

Ans: The given statement is “A linear equation \[2x + 3y = 5\] has a unique solution.”

\[2x + 3y = 5\]

$y = \dfrac{{5 - 2x}}{3}$

To find the solution of the linear equation \[2x + 3y = 5\], choose the random value of x to find the value of y.

A linear equation \[2x + 3y = 5\] has infinitely many solutions.

Hence, the given statement is “A linear equation \[2x + 3y = 5\] has a unique solution” is False.

(iii). All the points \[\left( {2, 0} \right),\left( {-\;3, 0} \right),\left( {4, 2} \right) \text{ and } \left( {0, 5} \right)\] lie on the \[x - \] axis.

Ans: The given statement is “All the points \[\left( {2,{\text{ }}0} \right),\left( {-\;3,{\text{ }}0} \right),\left( {4,{\text{ }}2} \right){\text{ and }}\left( {0,{\text{ }}5} \right)\] lie on the \[x - \]axis.”

On the \[x - \] axis, y-coordinate = 0.

The points \[\left( {4,{\text{ }}2} \right){\text{ and }}\left( {0,{\text{ }}5} \right)\] does not lie on \[x - \] axis as there y-coordinate \[ \ne \] 0.

Hence, the given statement is “All the points \[\left( {2,{\text{ }}0} \right),\left( {-\;3,{\text{ }}0} \right),\left( {4,{\text{ }}2} \right){\text{ and }}\left( {0,{\text{ }}5} \right)\] lie on the \[x - \] axis.” Is false.

(iv) The line parallel to the \[\;y - \]axis at a distance 4 units to the left of \[y - \]axis is given by the equation \[x = -\;4.\] 

Ans:  The given statement is “The line parallel to the \[\;y - \]axis at a distance 4 units to the left of \[y - \]axis is given by the equation \[x = -\;4.\]”

We know that:

The line parallel to \[y - \]axis at distance $a$ units to the left of \[y - \]axis is given by the equation \[x = -a\] .

Hence, the given statement “The line parallel to the \[\;y - \]axis at a distance 4 units to the left of \[y - \]axis is given by the equation \[x = -\;4.\]”

(v) The graph of the equation \[y = mx + c\] passes through the origin.

Ans: The given statement is “If the line equation \[y = mx + c\] passes through the origin, it must satisfy the equation of the line.”

We know that:

If the line equation \[y = mx + c\] passes through the origin, it must satisfy the equation of the line.

Put \[x = 0,{\text{ }}y = 0\] 

\[\Rightarrow c = 0\]

\[x = 0,{\text{ }}y = 0\] does not satisfy the equation .

Hence, the given statement is “If the line equation \[y = mx + c\] passes through the origin, it must satisfy the equation of line.” is wrong.

2. Write whether the following statement is True or False? Justify your answer. The coordinates of points given in the table:

Represent some of the solutions of the equation \[2x + 2 = y\] .

Ans: Substituting the given values both coordinates of the given table in \[2x + 2 = y\]

For $\left( 0, 2 \right)$

${\text{LHS  = }}2x + 2$

${\text{         =  }}2(0) + 2$

${\text{         =  2}}$

${\text{ RHS}} = y$

${\text{        }} = 2$

${\text{LHS = RHS}}$

Hence,(0, 2) is the solution of the Linear equation 2x + 2 = y .

For $\left(1, 4 \right)$

${\text{LHS  =  }}2x + 2$

${\text{         = }}2(1) + 2$

${\text{         =  }}4$

${\text{RHS  =  y}}$

${\text{         =  4}}$

${\text{LHS = RHS}}$ 

Hence, (1,4) is the solution of the Linear equation \[2x + 2 = y\].

For $\left( 2, 6 \right)$

${\text{LHS  =  }}2x + 2$

${\text{         =  }}2(2) + 2$

${\text{       }} = 6$

${\text{RHS  =  y}}$

${\text{         =  6}}$

${\text{LHS}} = {\text{RHS}}$ 

Hence, (2, 6) is the solution of the Linear equation 2x + 2 = y .

For $\left( {3,8} \right)$

${\text{LHS}} = 2x + 2$

${\text{       }} = 2(3) + 2$

${\text{       }} = 8$

$ {\text{RHS  =  y}}$

${\text{          =  8}}$

${\text{LHS  =  RHS}}$ 

Hence, ( 3, 8) is the solution of the Linear equation 2x + 2 = y .

For $\left( 4, 10 \right)$

${\text{LHS}} = 2x + 2$

${\text{       }} = 2(4) + 2$

${\text{       }} = 10$

${\text{RHS  =  y}}$

${\text{          =  10}}$

${\text{LHS  =  RHS}}$ 

Hence, (4, 10) is the solution of the Linear equation 2x+2=y .

Exercise 4.2

Write whether the following statements are True or False? Justify your answers :

1. The point \[\left( {0, 3} \right)\] lies on the graph of the linear equation \[3x + 4y = 12\] . 

Ans: True

The linear equation is \[3x + 4y = 12\].

If the point \[\left( {0,{\text{ }}3} \right)\] satisfies the linear equation \[3x + 4y = 12\], then the point \[\left( {0,{\text{ }}3} \right)\] lies on the graph of the linear equation\[3x + 4y = 12\].

Put  \[x = 0,y = 3\] in the linear equation \[3x + 4y = 12\] .

$ {\text{LHS}} = 3x + 4y$

${\text{         = }}3(0) + 4(3)$

${\text{         = }}12$

${\text{RHS  =  12}}{\text{.}}$

${\text{LHS  =  RHS}}$ 

The point \[\left( {0,{\text{ }}3} \right)\] satisfies the linear equation \[3x + 4y = 12\].

The point \[\left( {0,{\text{ }}3} \right)\] lies on the graph of the linear equation \[3x + 4y = 12\] . 

2. The graph of the linear equation \[x + 2y = 7\] passes through the point \[\left( {0, 7} \right)\]. 

Ans: False

The point \[\left( {0, 7} \right)\] and the linear equation \[x + 2y = 7\].

If the point \[\left( {0,{\text{ }}7} \right)\] satisfies the linear equation \[x + 2y = 7\], then the graph of the linear equation \[x + 2y = 7\] passes through the point \[\left( {0,{\text{ }}7} \right)\].

Put \[x = 0,y = 7\] in the linear equation \[x + 2y = 7\].

${\text{LHS}} = x + 2y$

${\text{         =  }}(0) + 2(7)$

${\text{         = }}14$

${\text{RHS}} = 7$

${\text{LHS }} \ne {\text{ RHS}}$ 

The point \[\left( {0,{\text{ }}7} \right)\] does not satisfy the linear equation \[x + 2y = 7\].

Hence, the graph of the linear equation \[x + 2y = 7\] does not pass through the point \[\left( {0,{\text{ }}7} \right)\].

3. The graph given below represents the linear equation \[x + y = 0\] .

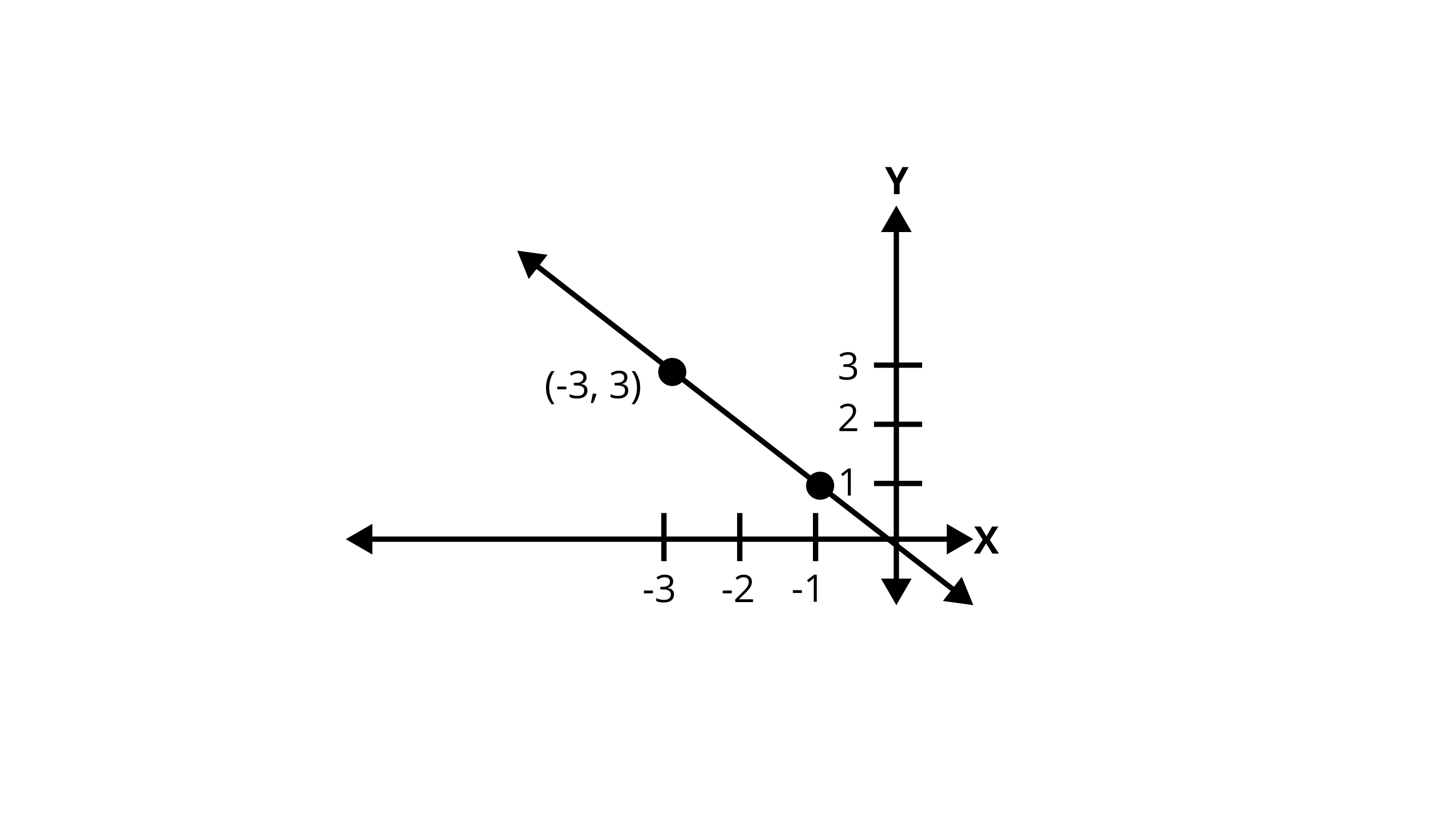
Ans:  True.

The points on the graph are $\left( { - 1,1} \right)\,{\text{and}}\;\left( { - 3,3} \right)$. 

\[\Rightarrow \] The coordinates are opposite in sign.

For the line \[x + y = 0\],

The coordinates are opposite in sign.

Hence, the given graph represents the linear equation \[x + y = 0\].

4. The graph given below represents the linear equation \[x = 3\]. 

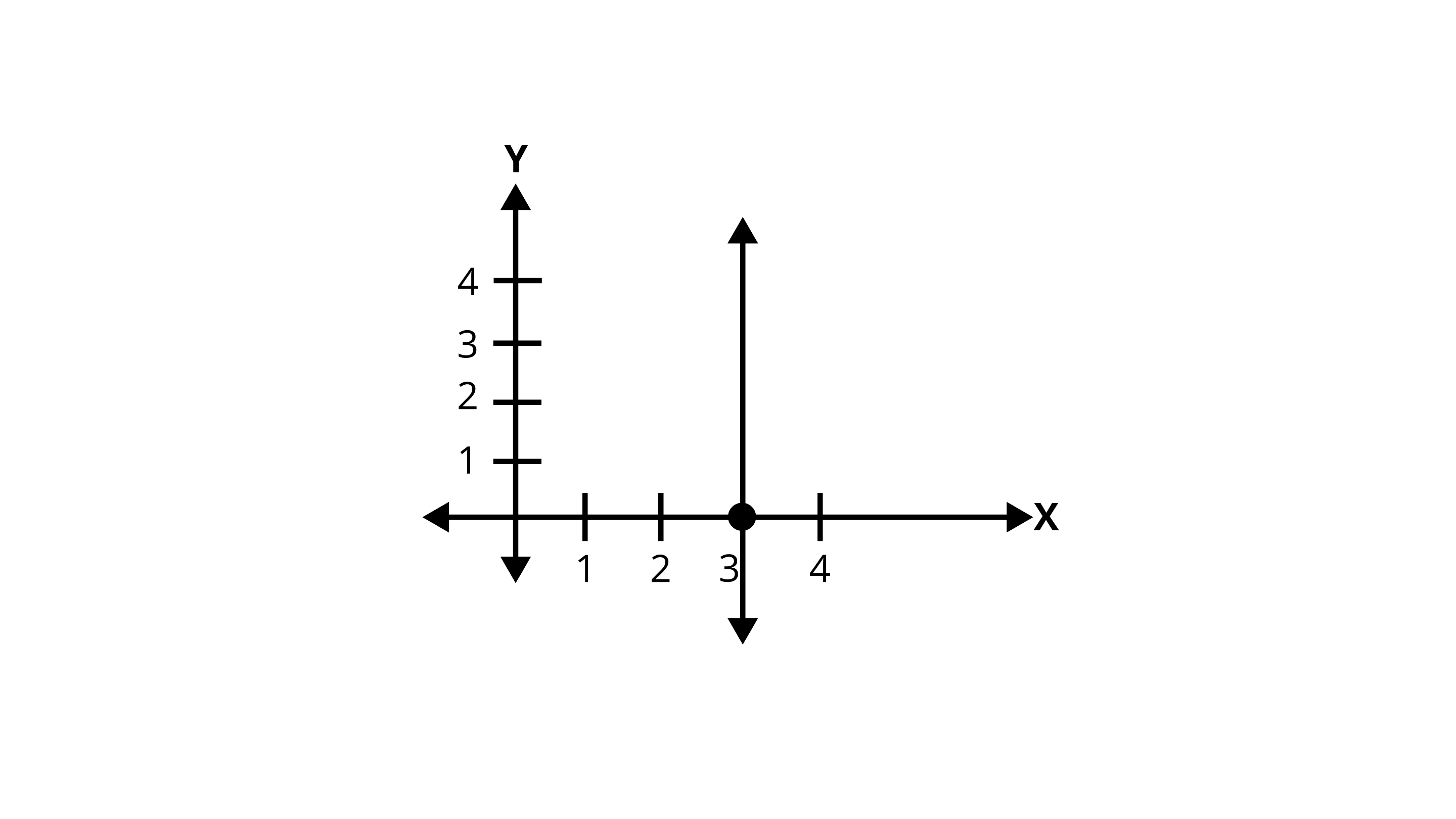
Ans: True

From the graph, it is observed that the line is parallel to the $y -$axis at a distance 3 units to the right of origin.

We know that:

The line parallel to \[y - \]axis at distance $a$ units to the right of \[y - \]axis is given by the equation \[x = 3\].

5. The coordinates of points in the table:

Represent some of the solutions of the equation \[x-y + 2 = 0.\] 

Ans: False

Substituting the given values both coordinates of the given table in \[2x + 2 = y\]

For $\left( {0,2} \right)$

${\text{LHS}} = x-y + 2$

$= x - y + 2$

$= (0) - 2 + 2$

$= 0$

$= {\text{RHS}}$

${\text{LHS}}\;{\text{ = }}\;{\text{RHS}}$ 

Hence, (0, 2) is solution of the equation \[x-y + 2 = 0.\]

For $\left( {1, 3} \right)$

${\text{LHS}} = x-y + 2$

$= (1) - 3 + 2$

$= 0$

$= {\text{RHS}}$

${\text{LHS}}\;{\text{ = }}\;{\text{RHS}}$ 

Hence, (1, 3) is solution of the equation \[x-y + 2 = 0.\]

For $\left( {2,4} \right)$

${\text{LHS}} = x-y + 2$

$= (2) - 4 + 2$

$= 0$

$= {\text{RHS}}$

${\text{LHS}}\;{\text{ = }}\;{\text{RHS}}$

Hence, (2, 4) is solution of the equation \[x-y + 2 = 0.\]

For $(3, - 5)$

${\text{LHS}} = x-y + 2$

$\Rightarrow (3) - \left( { - 5} \right) + 2$

$\Rightarrow 10$

${\text{RHS}} = 0$

${\text{LHS}} \ne {\text{RHS}}$ 

Hence, (3, -5) is not solution of the equation \[x-y + 2 = 0.\]

For $\left( {4,6} \right)$

${\text{LHS}} = x-y + 2$

$= (4) - 6 + 2$

$= 0$

$= {\text{RHS}}$

${\text{L}}{\text{.H}}{\text{.S}}\;{\text{ = }}\;{\text{R}}{\text{.H}}{\text{.S}}$ 

Hence, (4,6 ) is solution of the equation \[x-y + 2 = 0.\]

6. Every point on the graph of a linear equation in two variables does not represent a solution of the linear equation.

Ans: False.

Every point on the graph of a linear equation in two variables represents a solution of the linear equation.

7. The graph of every linear equation in two variables need not be a line.

Ans: False.

The graph of every linear equation in two variables

The graph of every linear equation in two variables need not be a line.

Sample Questions

1. Find the points where the graph of the equation \[3x + 4y = 12\]  cuts the \[x - \] axis and the \[y - \] axis.

Ans: \[3x + 4y = 12\] cuts the \[x - \] axis at the point where $y = 0$ 

Substituting the $y = 0$ in \[3x + 4y = 12\]

$3x + 4y = 12$

$\Rightarrow 3x + 4(0) = 12$

$\Rightarrow 3x = 12$

$\Rightarrow x = 4$ 

The required point is $\left( {4,0} \right)$.

\[3x + 4y = 12\]  cuts the \[y - \] axis at the point where $x = 0$

$3x + 4y = 12$

$\Rightarrow 3(0) + 4y = 12$

$\Rightarrow 4y = 12$

$\Rightarrow y = 3$ 

The required point is $\left( {0,3} \right)$.

2. At what point does the graph of the linear equation \[x + y = 5\] meet a line which is parallel to the \[y - \] axis, at a distance 2 units from the origin and in the positive direction of \[x - \] axis.

Ans: A line which is parallel to the \[y - \] axis, at a distance ‘2’ units from the origin and in the positive direction of \[x - \] axis.

x = 2

Let the point be $\left( {2,y} \right)$ 

Substituting the value $x = 2\;$ in the linear equation \[x + y = 5\;.\]

$x + y = 5$

$\Rightarrow 2 + y = 5$

$\Rightarrow y = 5 - 2$

$\Rightarrow y = 3$ 

The required point is $\left( {2,3} \right)$.

3. Determine the point on the graph of the equation \[2x + 5y = 20\] whose \[x - \] coordinate is \[\dfrac{5}{2}\] times its ordinate.

Ans: We have:

\[x - \] Coordinate is \[\dfrac{5}{2}\] times its ordinate

This implies $x = \dfrac{5}{2}y$ 

Substituting the above value in linear equation \[2x + 5y = {\text{2}}0\]

$2x + 5y = {\text{2}}0$

$\Rightarrow 2\left( {\dfrac{5}{2}y} \right) + 5y = 20$

$\Rightarrow 5y + 5y = 20$

$\Rightarrow 10y = 20$

$\Rightarrow y = 2$ 

So,

$\Rightarrow x = \dfrac{5}{2}\left( 2 \right)$

$\Rightarrow x = 5$ 

The required point is $\left( {5,2} \right)$.

4. Draw the graph of the equation represented by the straight line which is parallel to the \[x - \] axis and is 4 units above it.

Ans: Any straight line parallel to \[x - \] axis is given by \[y = k\], where \[k\] is the distance of the line from the \[x - \] axis.

$\Rightarrow y = 4$

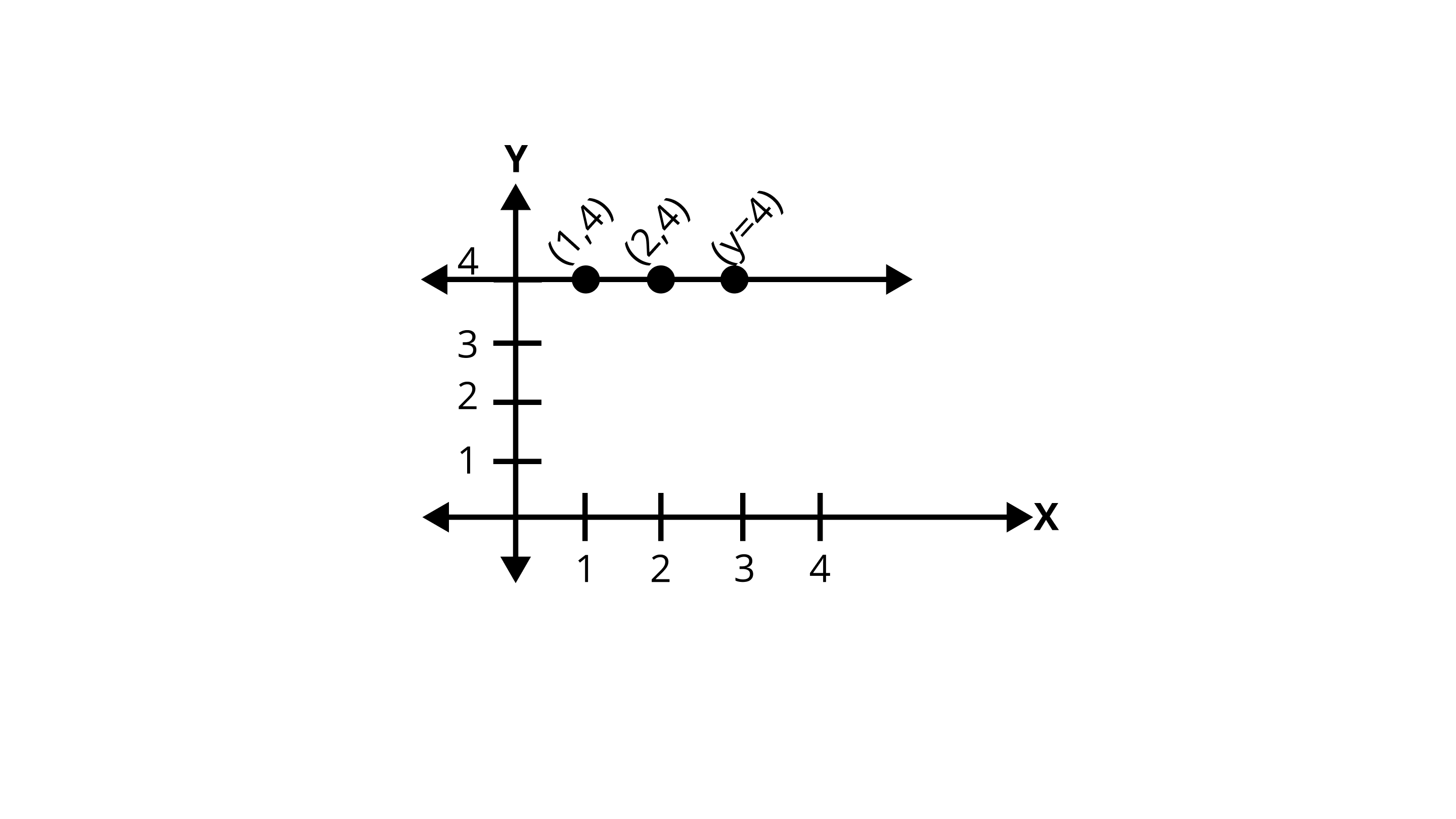
Exercise 4.3

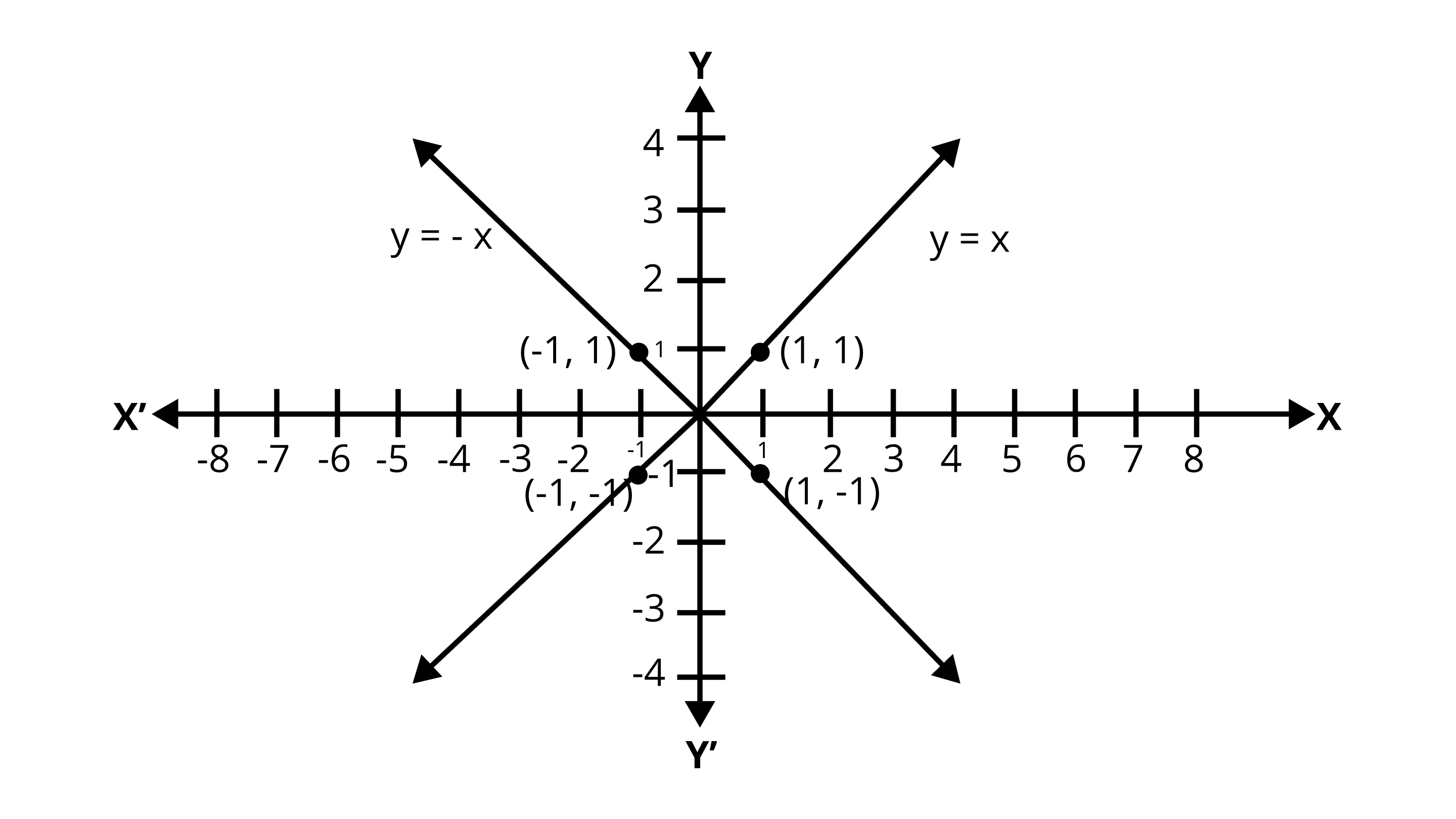
1.  Draw the graphs of linear equations \[y = x \text{ and }y = -x\] on the same cartesian plane. What do you observe?

Ans: For \[y = x\]

Substituting different values of $x$ to get different values of $y$ 

For \[y =  - \;x\]

Substituting different values of $x$ to get different values of $y$ 

Plot the points on the graph paper and join the lines.

2. Determine the point on the graph of the linear equation \[2x + 5y = 19,\] whose ordinate is \[1 \dfrac{1}{2} \]  times its abscissa.

Ans: Ordinate is \[1{\text{ }}\dfrac{1}{2}{\text{ }}\]  times its abscissa

This implies $y = 1\dfrac{1}{2}x = \dfrac{3}{2}x$ 

Substituting the above value in linear equation \[2x + 5y = 19\]

$2x + 5y = 19,$

$\Rightarrow 2x + 5\left( {\dfrac{3}{2}x} \right) = 19$

$\Rightarrow 2x + \dfrac{{15}}{2}x = 19$

$\Rightarrow \dfrac{{4x + 15x}}{2} = 19$

$\Rightarrow \dfrac{{19x}}{2} = 19$

$\Rightarrow x = 2$  

So, 

$\Rightarrow y = \dfrac{3}{2}x$

$\Rightarrow y = \dfrac{3}{2}(2)$

$\Rightarrow y = 3$ 

The required point is $\left( {2,3} \right)$.

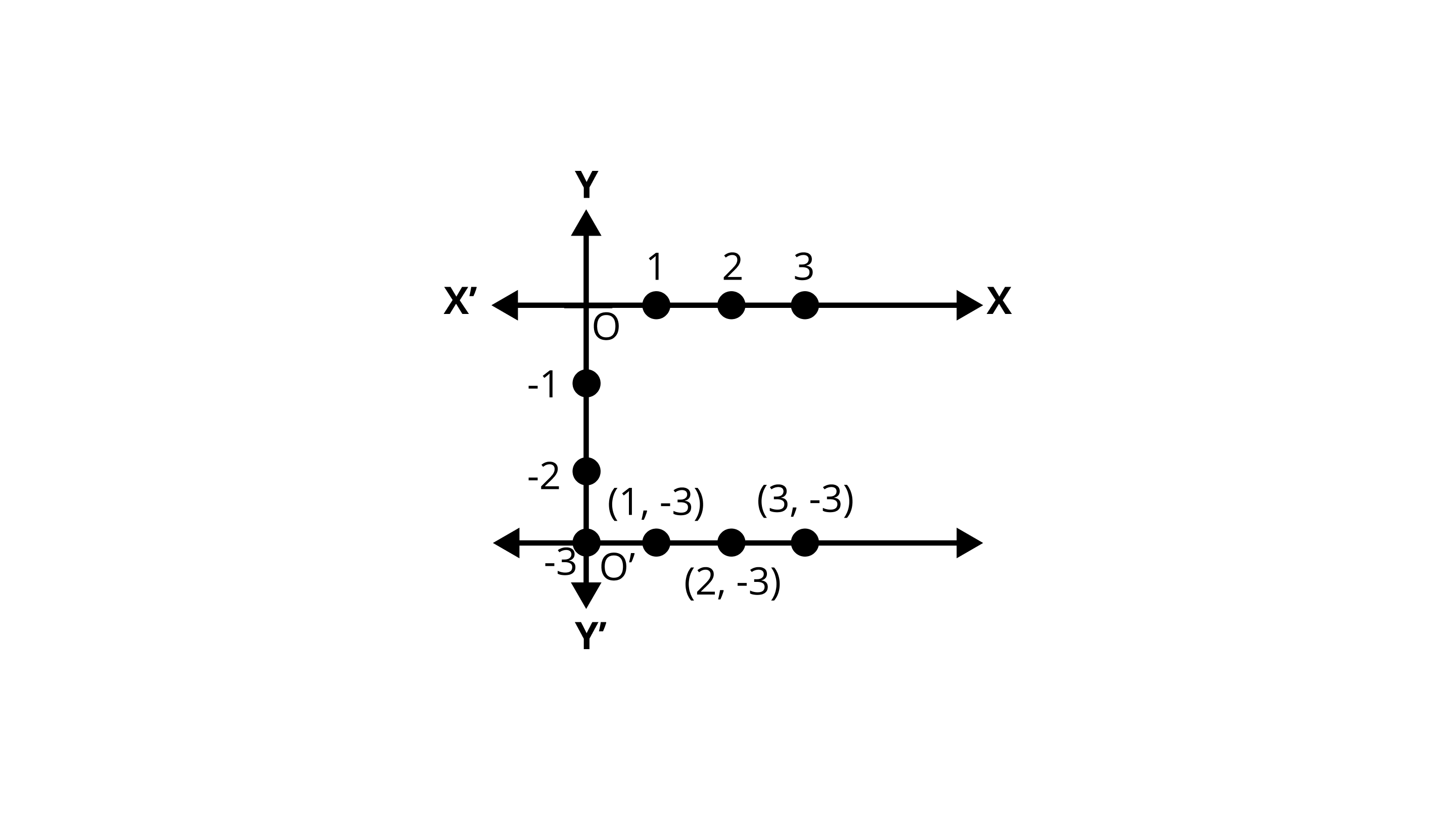
3. Draw the graph of the equation represented by a straight line which is parallel to the \[x - \] axis and at a distance 3 units below it.

Ans: We know that:

Any straight line parallel to \[x - \] axis is given by \[y = k\] , where \[k\] is the distance of the line from the \[x - \] axis.

The line is parallel to the \[x - \]  axis and at a distance 3 units below it.

$\therefore \;y =  - 3$

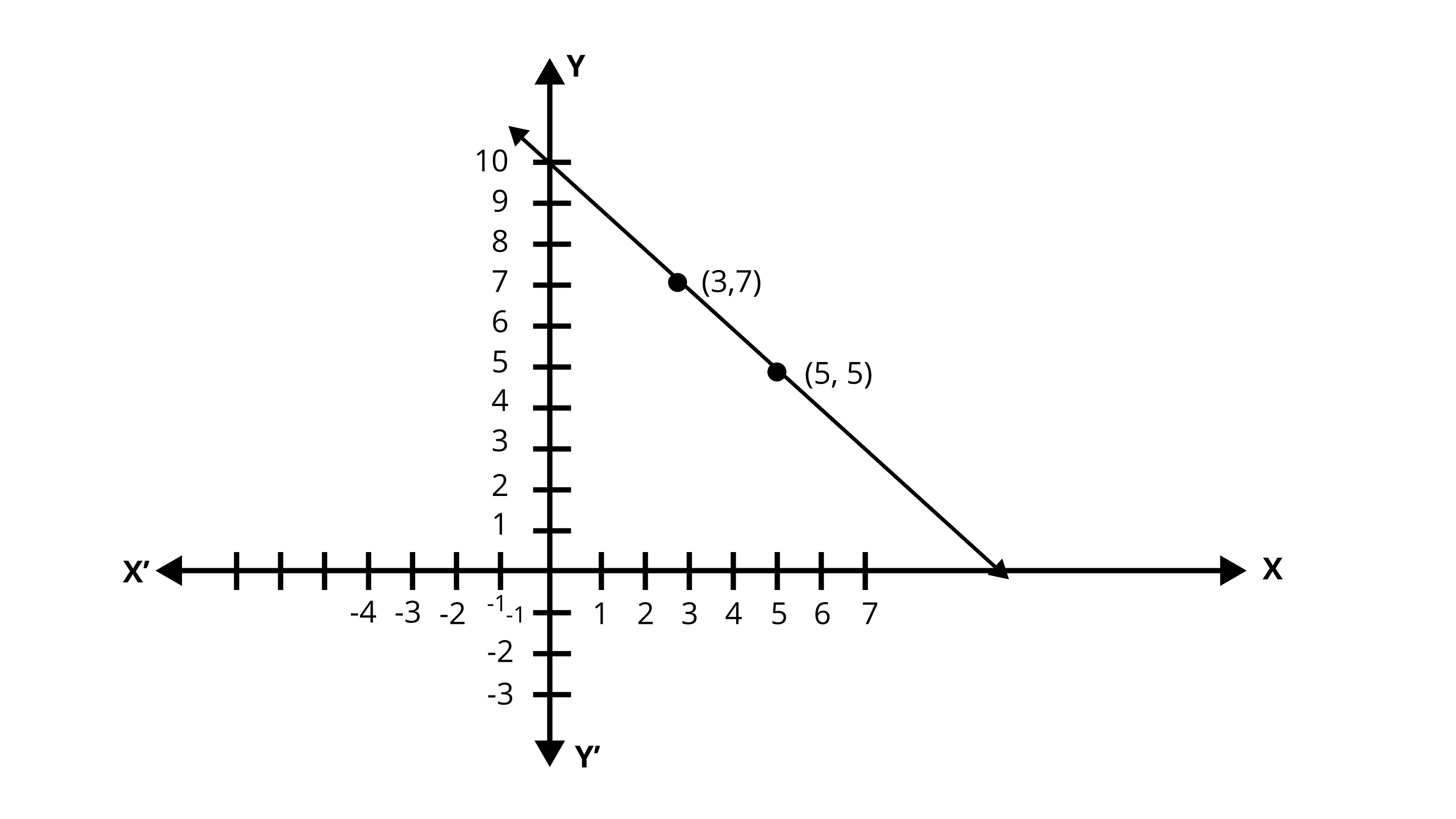
4. Draw the graph of the linear equation whose solutions are represented by the points having the sum of the coordinates as 10 units.

Ans: Since, the points having the sum of the coordinates as 10 units.

The linear equation must be \[x + y = 10\] 

For \[x = 5,{\text{ }}y = 5,\] therefore, \[\left( {5,{\text{ }}5} \right)\] lies on the graph of \[x + y = 10\].
For \[x = 3,{\text{ }}y = 7\] , therefore, \[\left( {3,{\text{ }}7} \right)\] lies on the graph of \[x + y = 10\].

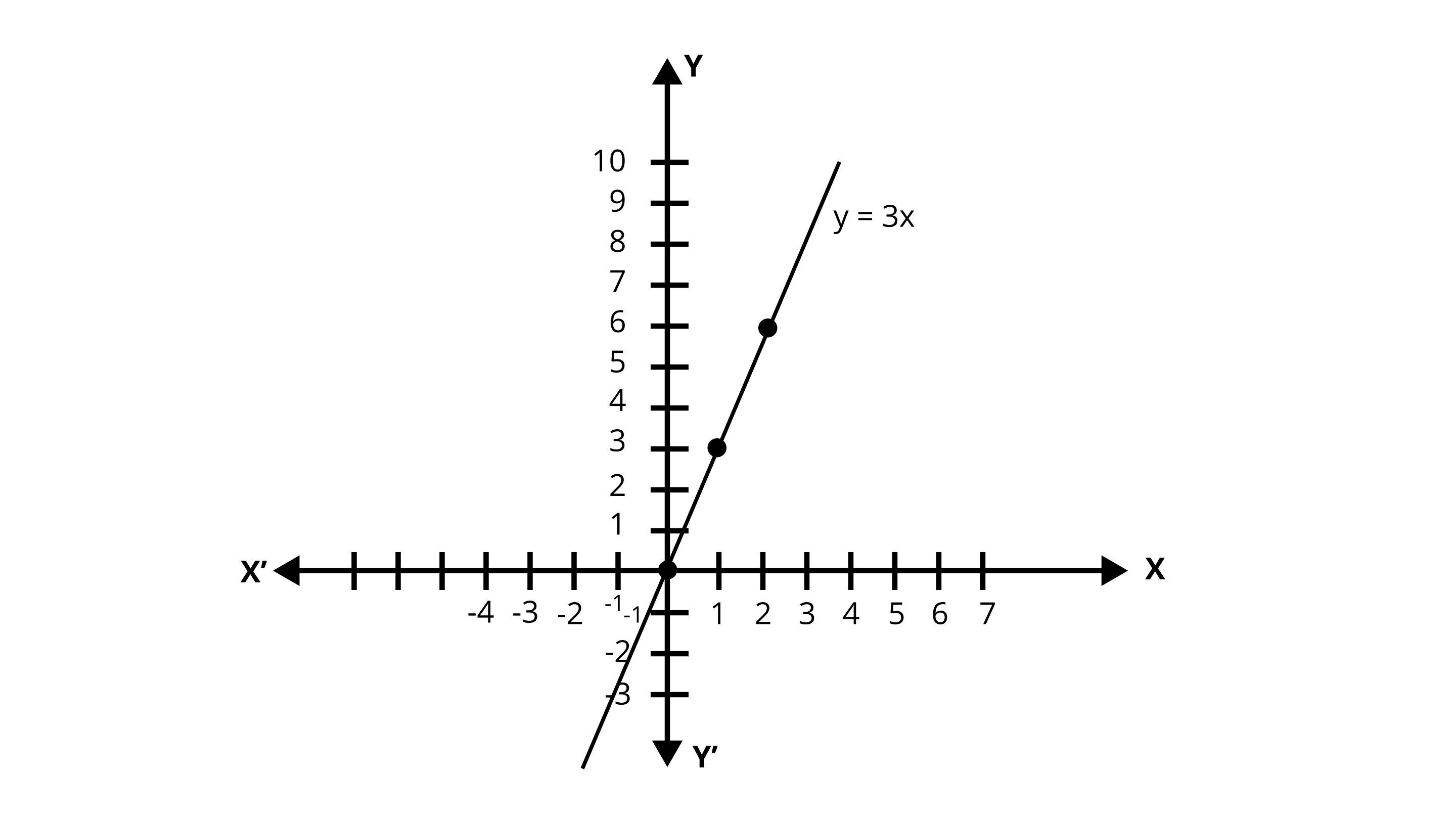
5. Write the linear equation such that each point on its graph has an ordinate 3 times its abscissa.

Ans: Suppose the abscissa be $x$.

Ordinate \[\left( y \right) = 3{\text{ }}x\] 

An ordinate 3 times its abscissa.

\[\Rightarrow {\text{ }}y = 3x\] 

Substituting the values of$x$ to get the values of $y$

6. If the point \[\left( {3, 4} \right)\] lies on the graph of \[3y = ax + 7,\] then find the value of \[a\;.\] 

Ans: The point \[\left( {3,{\text{ }}4} \right)\] lies on the graph of \[3y = ax + 7\;.\]

This implies \[\left( {3,{\text{ }}4} \right)\] should satisfy the linear equation \[3y = ax + 7.\]

${\text{Put }}x = 3,\;y = 4{\text{ we get:}}$

$3y = ax + 7$

$\Rightarrow 3\left( 4 \right) = a\left( 3 \right) + 7$

$\Rightarrow 3a = 12 - 7$

$\Rightarrow a = \dfrac{5}{3}$ 

Hence, the value of a is $\dfrac{5}{3}$.

7. How many solution(s) of the equation \[2x + 1 = x-3\] are there on the:   

(i) Number line          (ii) Cartesian plane

Ans: The given equation is

$\Rightarrow 2x + 1 = x-3$

${\text{On simplification, we get:}}$

$\Rightarrow 2x - x =  - 3 - 1$

$\Rightarrow x =  - \;4$ 

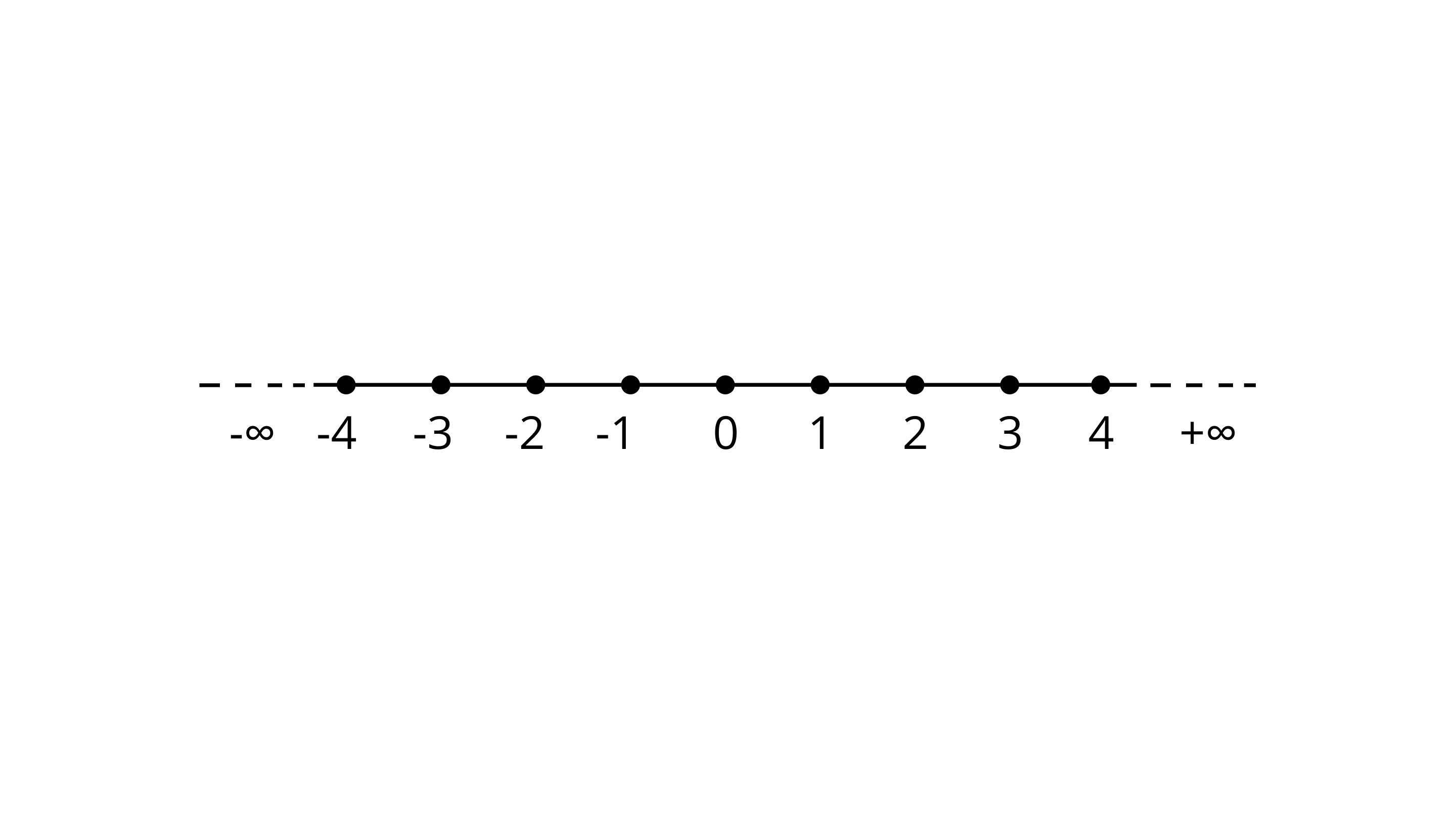
(i) Number Line: 

The solution of the equation \[2x + 1 = x-3\] on the Number line is \[x =  - 4\].

(ii) Cartesian plane:

The solution of the equation \[2x + 1 = x-3\] in Cartesian plane $x + 4 = 0$

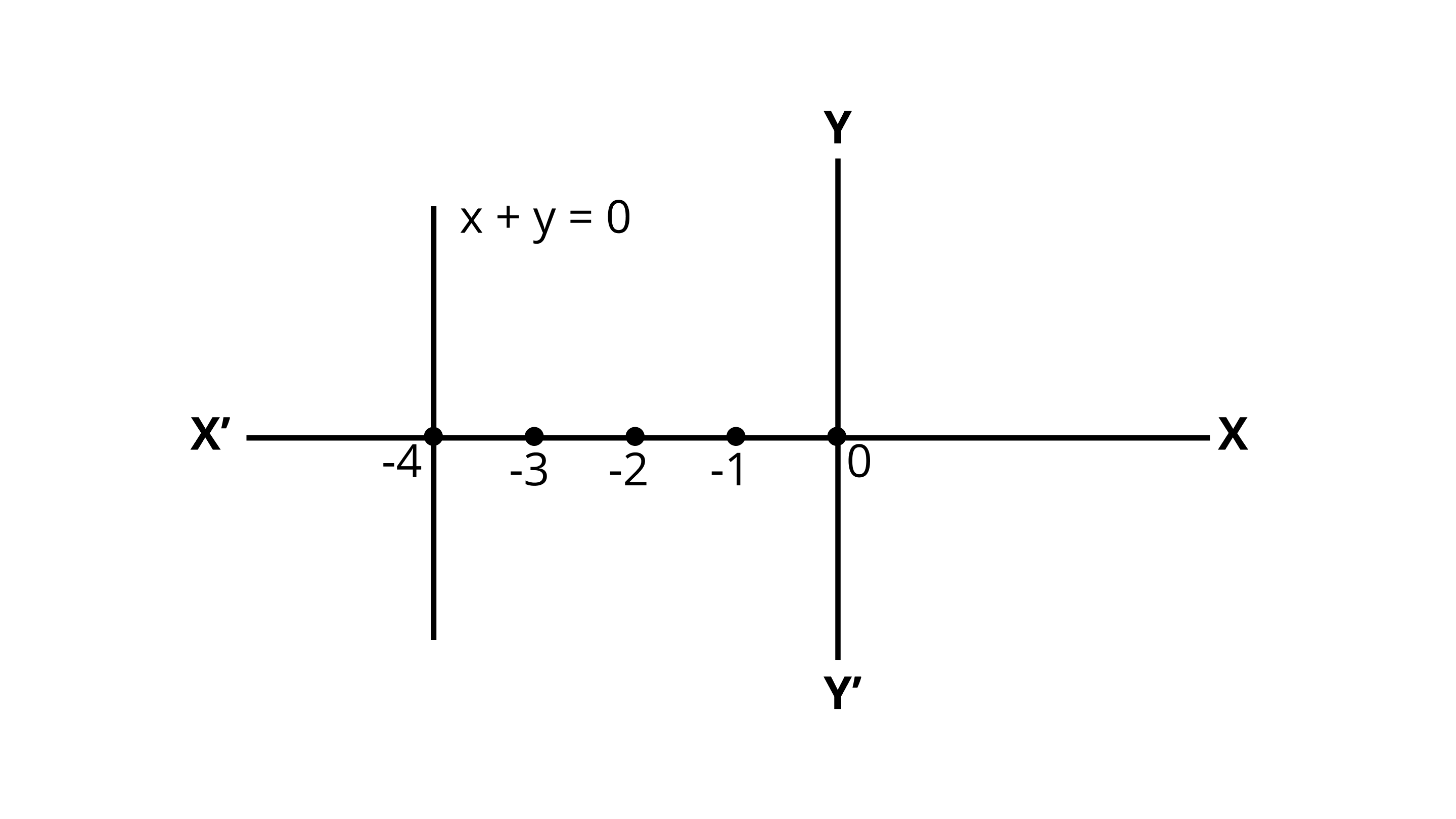
8. Find the solution of the linear equation \[x + 2y = 8\] which represents a point on

(i)\[x-\]axis              (ii)\[y-\]axis 

Ans: The given linear equation is \[x + 2y = 8\].

(i) \[x - \]  axis   

On x – axis, y-coordinate = y = 0

$x + 2y = 8$

$\Rightarrow x + 2(0) = 8$

$\Rightarrow x = 8$ 

The required point is $\left( {8,0} \right).$

(ii)\[y - \]axis

On y – axis, x-coordinate = x = 0

$x + 2y = 8$

$\Rightarrow 0 + 2y = 8$

$\Rightarrow y = 4$ 

The required point is $\left( {0,4} \right).$ 

9. For what value of $c$ , the linear equation \[2x + cy = 8\] has equal values of $x$ and \[y\] for its solution.

Ans: The linear equation \[2x + cy = 8\] has equal values of $x$  and \[y\] for its solution.

Since, $x = y$ 

Substituting the value in \[2x + cy = 8\]

$ 2x + cy = 8$

$\Rightarrow 2x + c(x) = 8$

$\Rightarrow cx = 8 - 2x$

$\Rightarrow c = \dfrac{{8 - 2x}}{x},\;\;{\text{where }}x \ne {\text{ 0}}$ 

Hence, the value of c is \[\dfrac{{8 - 2x}}{x},\;\;{\text{where }}x \ne {\text{ 0}}\].

10. Let \[y\] varies directly as \[x\]. If \[y = 12\] when \[x = 4,\] then write a linear equation. What is the value of \[y\] when \[x = 5\] ?

Ans: Let \[y\] varies directly as\[x\].

$y \propto x$

$\Rightarrow y = kx..............{\text{(i)}}$

$y = 12\;{\text{and}}\;x = 4$

$\Rightarrow 12 = 4k$ 

\[\Rightarrow k = \dfrac{{12}}{4} = 3\]

Substituting the value of$k$ in equation (i), we get:

\[y = 3x\]

When \[x = 5\]

$ y = 3x$

$\Rightarrow y = 3(5)$

$\Rightarrow y = 15$ 

Sample Questions

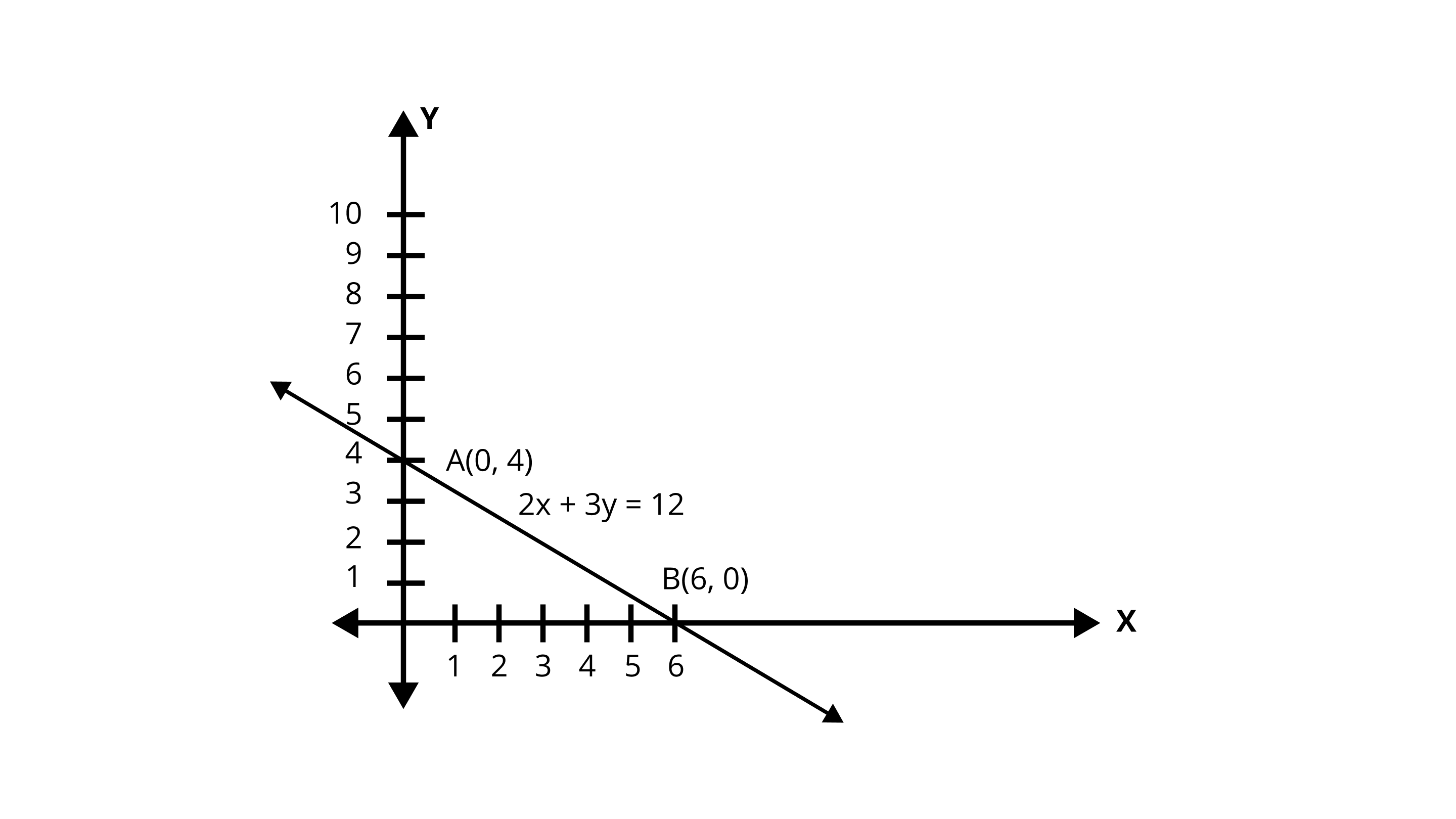
1. Draw the graph of the linear equation \[2x + 3y = 12\] . At what points, the graph of the equation cuts the \[x - \] axis and the \[y - \]axis?

Ans: The given equation is \[2x + 3y = 12\].

$3y = 12 - 2x$

$\Rightarrow y = \dfrac{{12 - 2x}}{3}.......{\text{(i)}}$ 

The Point at which the graph cuts the $x -$ axis 

On x – axis, $y = 0$ 

Put y = 0 in equation (i), we get:

$y = \dfrac{{12 - 2x}}{3}$

$\Rightarrow \dfrac{{12 - 2x}}{3} = 0$

$\Rightarrow 2x = 12$

$\Rightarrow x = 6$                            

The Point at which the graph cuts the $x -$ axis is $\left( {6,0} \right)$ .

The Point at which the graph cuts the $y -$ axis. 

On y – axis, $x = 0$

$y = \dfrac{{12 - 2x}}{3}$

$\Rightarrow y = \dfrac{{12 - 2(0)}}{3}$

$\Rightarrow y = 4$ 

The Point at which the graph cuts the $y -$ axis is $\left( {0,4} \right)$ . 

2. The following values of \[x\] and \[y\] are thought to satisfy a linear equation:

Draw the graph, using the values of \[x, y\] as given in the above table. At what point the graph of the linear equation (i) cuts the \[x - \]axis. (ii) cuts the \[y - \]axis.

Ans:

From the table, we have:

\[A\left( {1,{\text{ }}1} \right){\text{ and }}B\left( {2,{\text{ }}3} \right){\text{ }}\] 

In XY-plane, to plot any point, start at the origin. The x-coordinate tells you how far to go to the right (if positive) or left (if negative) along the x- axis. The y-coordinate you how far to go up (if positive) or down (if negative) along the y-axis.

Plotting the graph for the above points,

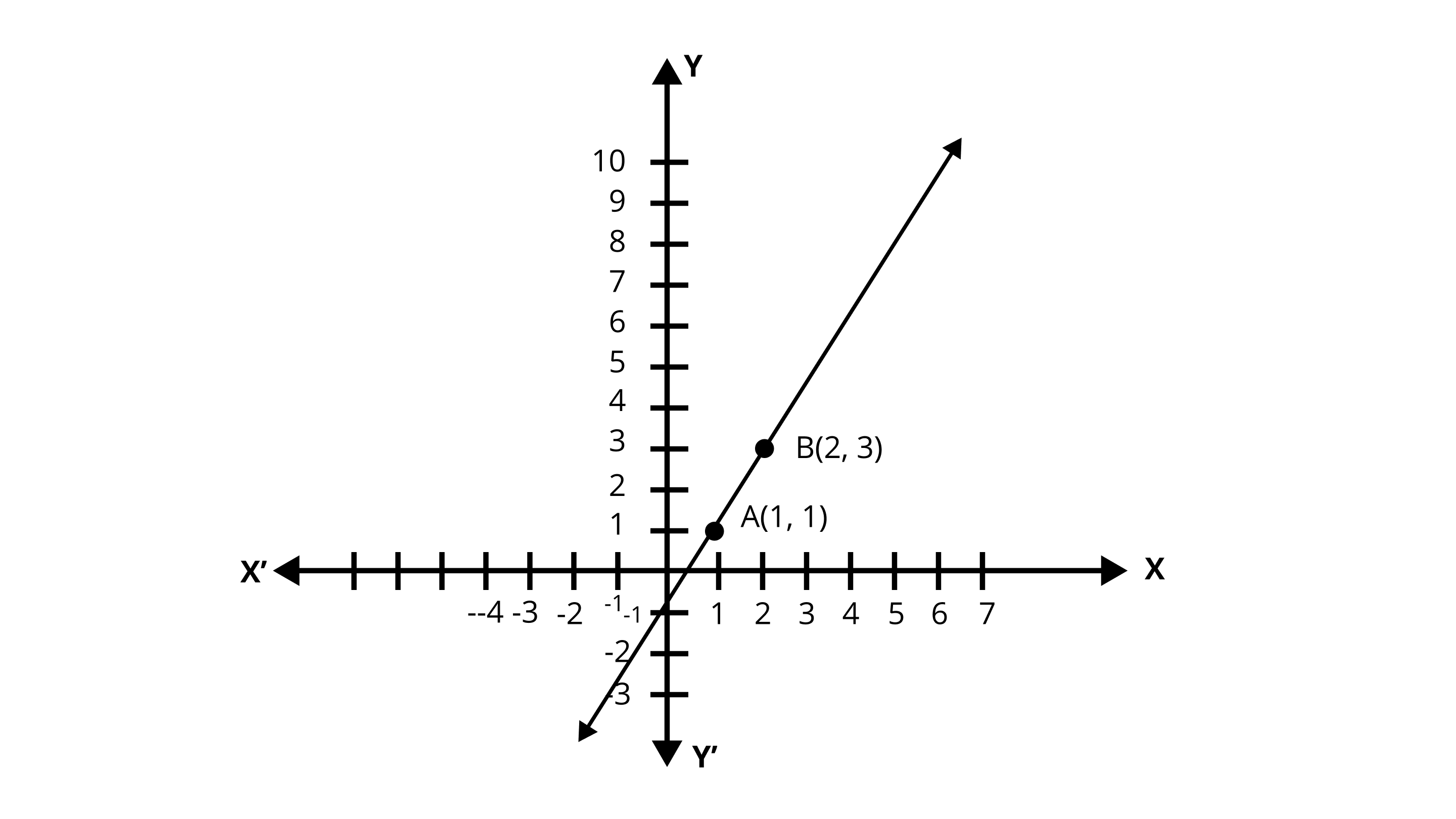
(i). From the graph the point where the straight line cuts the $x -$ axis is $\left( {\dfrac{1}{2},0} \right)$ .

(ii). From the graph the point where the straight line cuts the $y -$ axis is $\left( {0, - 1} \right)$ .

3. The Auto Rickshaw fare in a city is charged Rs 10 for the first kilometer and @ Rs 4 per kilometer for subsequent distance covered. Write the linear equation to express the above statement. Draw the graph of the linear equation.

Ans: Assume,

Total distance covered $ = x\;{\text{km}}$ 

Fare charged =$ {\text{Rs}}\;y$ 

Auto-rickshaw fare in a city for the first kilometer $ = {\text{Rs }}10$ 

Fare per kilometer for subsequent distance covered $ = {\text{Rs }}4$ 

This implies,

Remaining $\left( {x - 1} \right)\;{\text{km}}$ fare charged \[ = {\text{Rs }}4\left( {x-1} \right)\] 

So, 

$\Rightarrow y = 10 + 4\left( {x-1} \right)$

$\Rightarrow y = 4x + 6{\text{ }}$ 

The required linear equation is \[y = 4x + 6\].

At \[x = 0,{\text{ }}y = 6{\text{ }}\] and \[x = -1,{\text{ }}y = 2\]

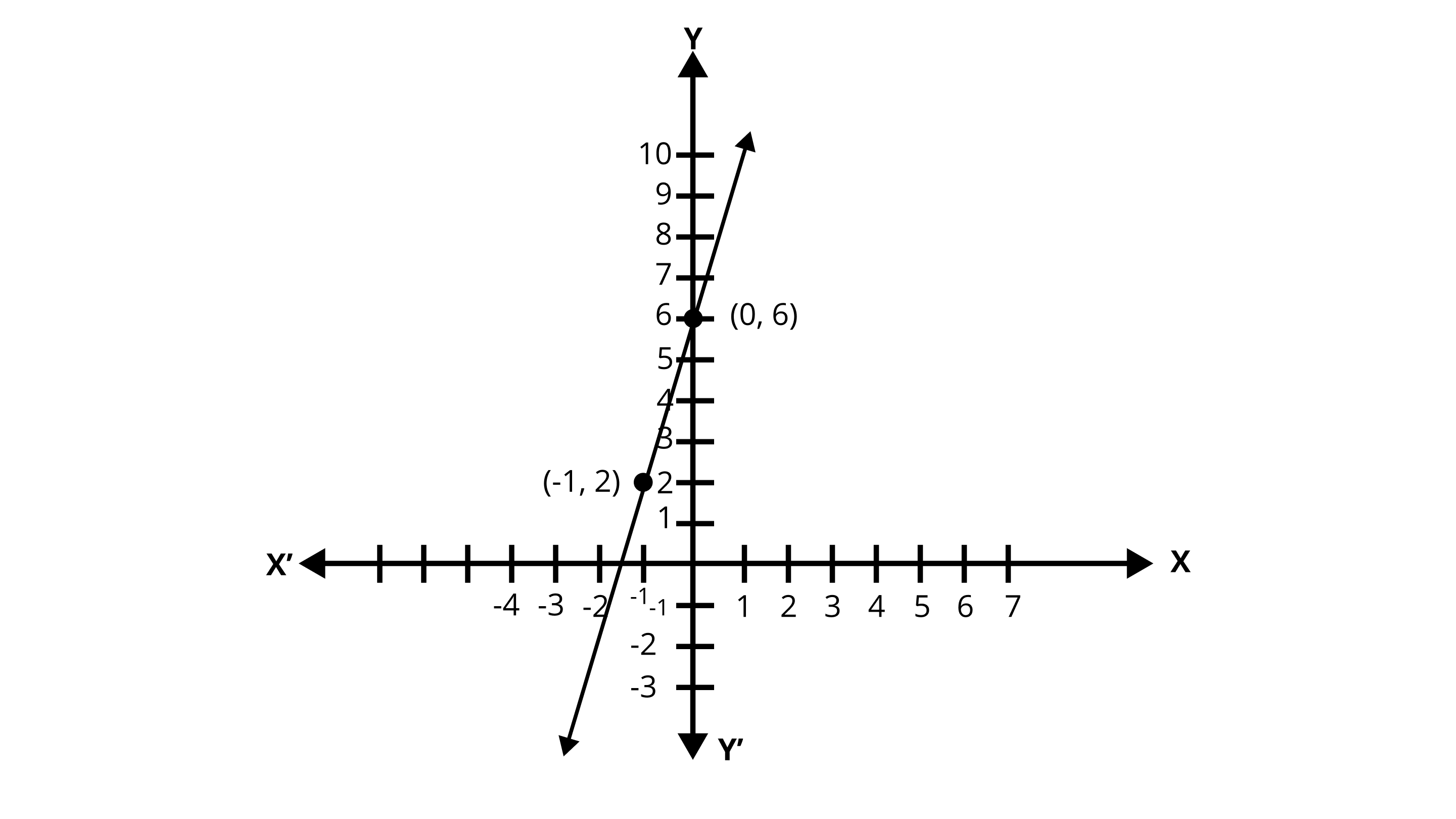
4. The work done by a body on application of a constant force is the product of the constant force and the distance travelled by the body in the direction of force. Express this in the form of a linear equation in two variables and draw its graph by taking the constant force as 3 units. What is the work done when the distance travelled is 2 units? Verify it by plotting the graph.

Ans: ${\text{Work done  =  }}\left( {{\text{constant force}}} \right) \times \left( {{\text{distance}}} \right)$

${\text{work done  =  }}3 \times \;{\text{distance}}$

${\text{Assume that y is the work done and }}{\text{ x is the distance}}.$

$\Rightarrow y = 3x$ 

$x = 2$ (Given)

Work done $ = 3 \times 2 = 6\;{\text{units}}$ 

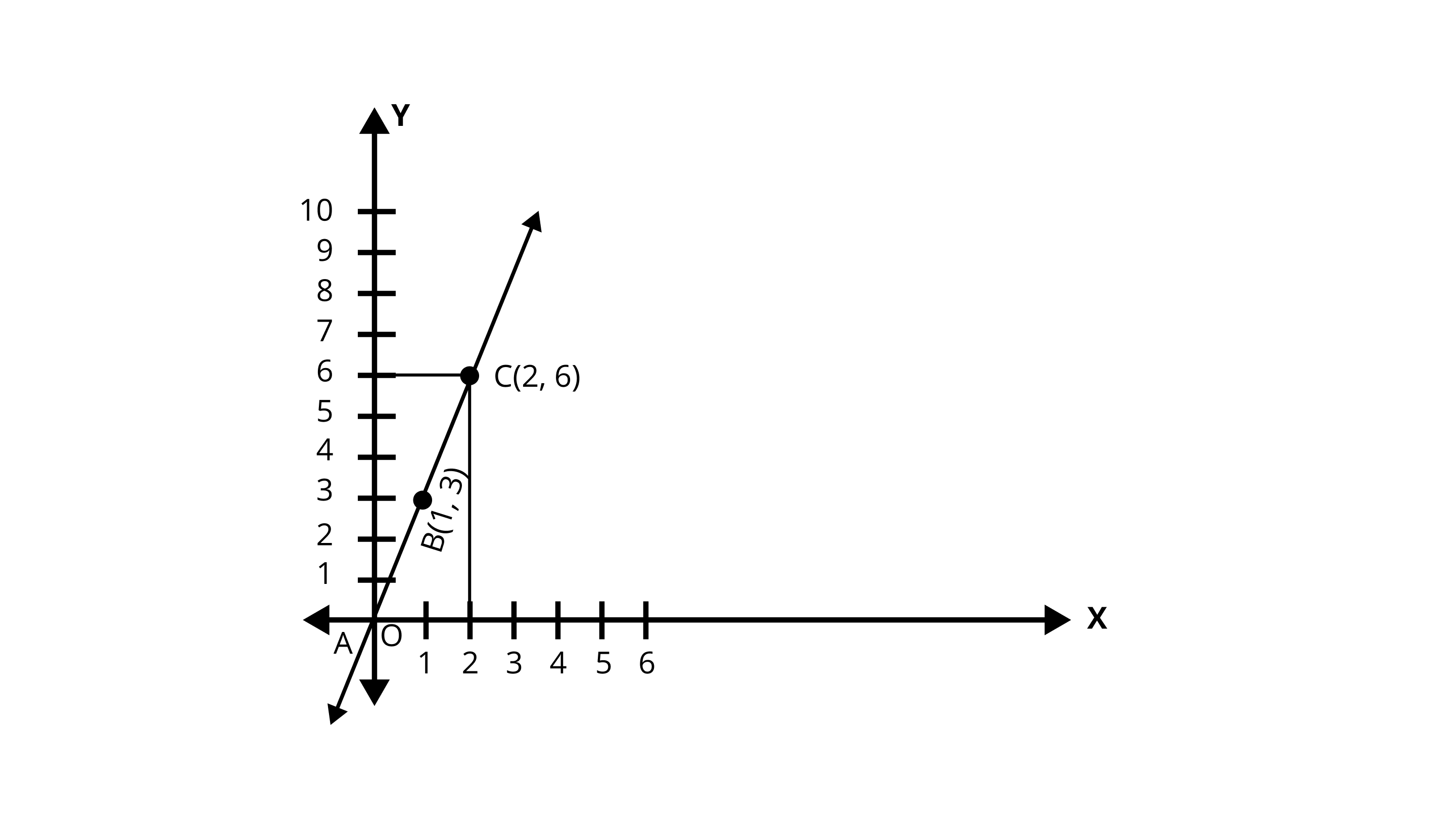
Exercise 4.4

1. Show that the points \[A\left( {1, 2} \right), B\left( {- 1,-16} \right) \text{ and }C\left( {0,-7} \right)\] lie on the graph of the linear equation \[y = 9x-7\] .

Ans: Substituting the values \[A\left( {1,{\text{ }}2} \right),{\text{ }}B\left( {-{\text{ }}1,-16} \right){\text{ and }}C\left( {0,-7} \right)\] in the linear equation\[y = 9x-7\] .

For\[A\left( {1,{\text{ }}2} \right)\]                                                                    

$y = 9x-7$

${\text{RHS}}{\text{ }} = y = 2$

${\text{LHS}} = 9(1) - 7$

$\Rightarrow {\text{          =  }}2$

${\text{LHS}}\;{\text{ = }}\;{\text{RHS}}$                                                      

The point \[A\left( {1,{\text{ }}2} \right)\] satisfies the linear equation\[y = 9x-7\], then the point \[A\left( {1,{\text{ }}2} \right)\] lies on the graph of the linear equation\[y = 9x-7\].

For \[B\left( { - 1,{\text{ }} - 16} \right)\]

$y = 9x-7$

${\text{RHS  =  y  =  }} - 16$

${\text{LHS}} = 9x-7$

${\text{         =  }}9( - 1) - 7$

${\text{       }} =  - 16$

${\text{LHS}}\;{\text{ = }}\;{\text{RHS}}$ 

The point \[B\left( { - 1,{\text{ }} - 16} \right)\] satisfies the linear equation\[y = 9x-7\], then the point \[B\left( { - 1,{\text{ }} - 16} \right)\] lies on the graph of the linear equation\[y = 9x-7\].

For \[C\left( {0,{\text{  - 7}}} \right)\]

$y = 9x-7$

${\text{RHS}} = y =  - 7$

${\text{LHS}} = 9x-7$

${\text{         =  }}9(0) - 7$

$\Rightarrow {\text{   }} =  - 7$

 ${\text{LHS}}\;{\text{ = }}\;{\text{RHS}}$ 

The point \[C\left( {0,-7} \right)\] satisfies the linear equation \[y = 9x-7\], then the point \[C\left( {0,-7} \right)\] lies on the graph of the linear equation \[y = 9x-7\].

2. The following observed values of \[x\] and \[y\] are thought to satisfy a linear equation. Write the linear equation:

Draw the graph using the values of \[x, y\] as given in the above table. At what points the graph of the linear equation (i) cuts the \[x - \]axis (ii) cuts the \[y - \]axis.

Ans: Two points from the table are \[A\left( {6, - \;2} \right){\text{ and }}B\left( { - \;6,6} \right){\text{ }}\].

Plotting the graph for the above points:

In XY-plane, to plot any point, start at the origin. The x-coordinate tells you how far to go to the right (if positive) or left (if negative) along the x- axis. The y-coordinate you how far to go up (if positive) or down (if negative) along the y-axis.

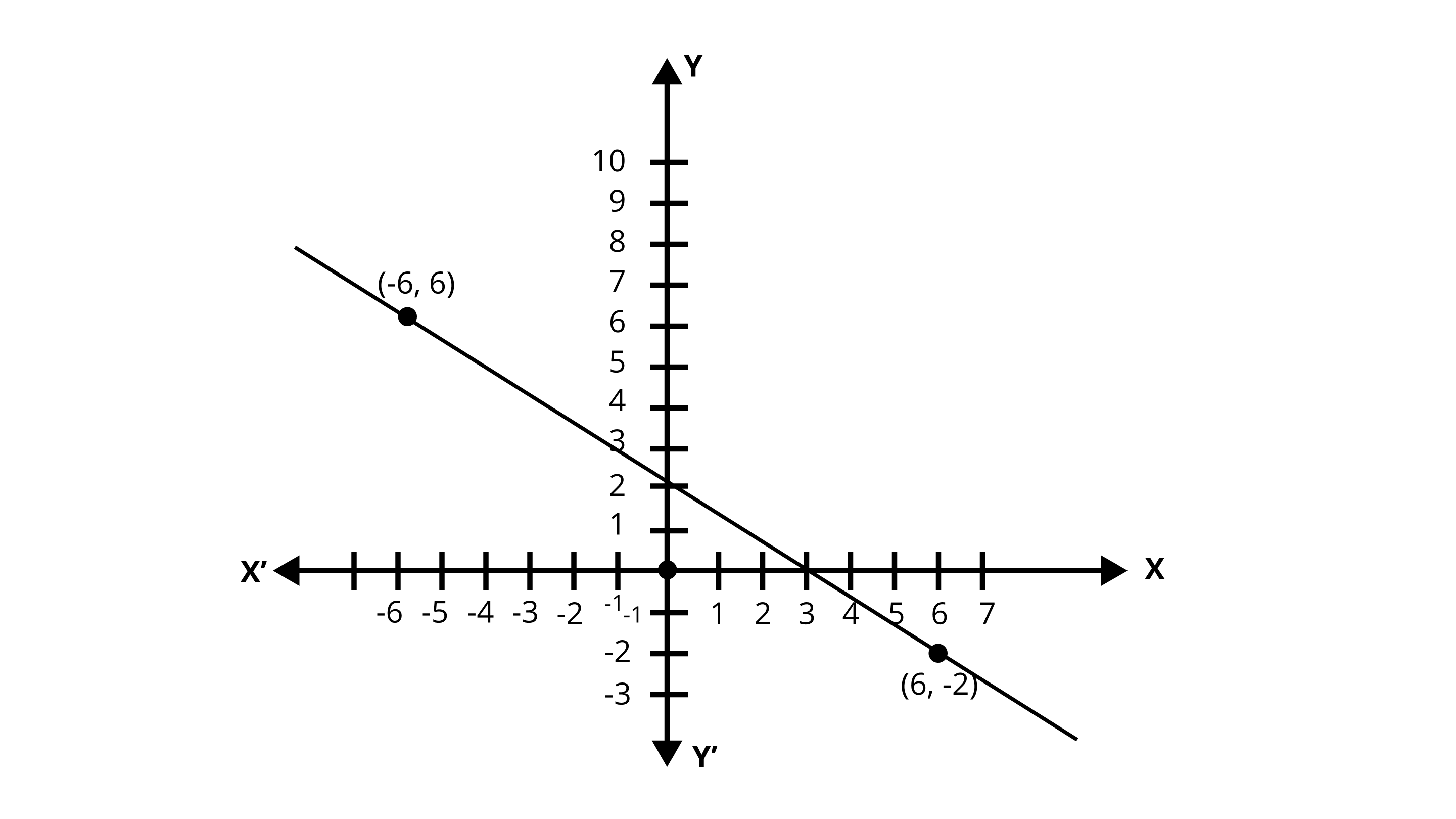
(i). From the graph the point where the straight line cuts the $x -$ axis is$\left( {3,0} \right)$ .

(ii). From the graph the point where the straight line cuts the $y -$ axis is$\left( {0,2} \right)$ .

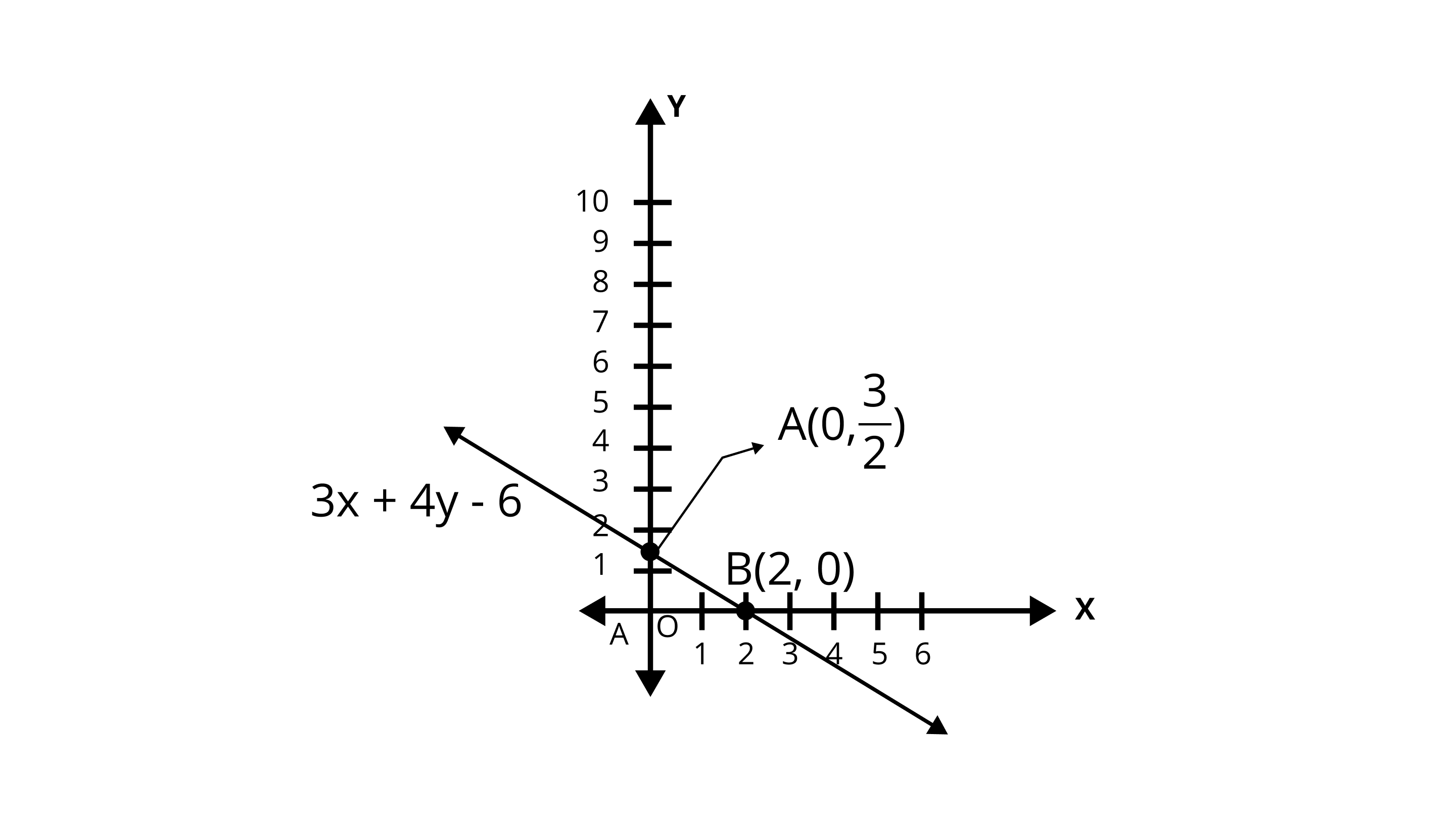
3. Draw the graph of the linear equation \[3x + 4y = 6\] . At what points, the graph cuts the \[x - \]axis and the \[y - \]axis.

Ans:  The given equation is \[3x + 4y = 6\]

On rearranging the terms, we get:

$4y = 6 - 3x$

$\Rightarrow y = \dfrac{{6 - 3x}}{4}$  

The graph cuts the $x -$ axis 

On x – axis, y- coordinate = 0

$3x + 4y = 6$

$\Rightarrow y = \dfrac{{6 - 3x}}{4}$

$\Rightarrow \dfrac{{6 - 3x}}{4} = 0$

$\Rightarrow 3x = 6$

$\Rightarrow x = 2$                           

The required point is $\left( {2,0} \right)$ .

On $y -$ axis, x – coordinate = 0 

$3x + 4y = 6$

$\Rightarrow y = \dfrac{{6 - 3x}}{4}$

$\Rightarrow y = \dfrac{{6 - 3(0)}}{4}$

$\Rightarrow y = \dfrac{3}{2}$ 

The required point is $\left( {0,\dfrac{3}{2}} \right)$ .

4. The linear equation that converts Fahrenheit (F) to Celsius (C) is given by the relation \[C = \dfrac{{5F - 160}}{9}\] 

(i). If the temperature is \[86^\circ F\], what is the temperature in Celsius? 

Ans: For \[86^\circ {\text{F}}\]

$\Rightarrow C = \dfrac{{5 \times 86 - 160}}{9}$

$\Rightarrow \dfrac{{430 - 160}}{9}$

$\Rightarrow \dfrac{{270}}{9} = {30^ \circ }{\text{C}}$ 

(ii). If the temperature is \[35^\circ C\], what is the temperature in Fahrenheit?

Ans: Rearranging the given equation

$\Rightarrow C = \dfrac{{5F - 160}}{9}$

$\Rightarrow 9C = 5F - 160$

$\Rightarrow 5F = 9C + 160$

$\Rightarrow F = \dfrac{{9C + 160}}{5}$ 

For \[35^\circ {\text{C}}\]

$\Rightarrow F = \dfrac{{9 \times 35 + 160}}{5}$

$\Rightarrow \dfrac{{315 + 160}}{5} = \dfrac{{475}}{5} = {95^ \circ }{\text{F}}$

(iii). If the temperature is \[0^\circ C\] what is the temperature in Fahrenheit and if the temperature is \[0^\circ F\], what is the temperature in Celsius?

Ans: For \[0^\circ {\text{C}}\]

$\Rightarrow F = \dfrac{{9 \times 0 + 160}}{5}$

$\Rightarrow \dfrac{{160}}{5} = {32^ \circ }{\text{F}}$ 

For \[0^\circ {\text{F}}\]

$\Rightarrow C = \dfrac{{5 \times 0 - 160}}{9}$

$\Rightarrow \dfrac{{ - 160}}{9} = {\left( { - \dfrac{{160}}{9}} \right)^ \circ }{\text{C}}$

(iv). What is the numerical value of the temperature which is the same in both the scales?

Ans: From the given condition above relation satisfies,

So,

$\Rightarrow C = \dfrac{{5C - 160}}{9}$

$\Rightarrow 9C = 5C - 160$

$\Rightarrow 9C - 5C =  - 160$

$\Rightarrow 4C =  - 160$

$\Rightarrow C = \dfrac{{ - 160}}{4}$

$\Rightarrow C =  - 40 = F$

5. If the temperature of a liquid can be measured in Kelvin units as \[x^\circ K\] or in Fahrenheit units as \[y^\circ F\] , the relation between the two systems of measurement of temperature is given by the linear equation \[y = \dfrac{9}{5}(x - 273) + 32\] 

(i). Find the temperature of the liquid in Fahrenheit if the temperature of the liquid is \[313^\circ K\] . 

Ans: Substituting \[x = 313^\circ {\text{K}}\] in the linear equation \[y = \dfrac{9}{5}(x - 273) + 32\]

$\Rightarrow y = \dfrac{9}{5}(313 - 273) + 32$

$= \dfrac{9}{5} \times 40 + 32$

$= 9 \times 8 + 32$

$= 72 + 32 = {104^ \circ }{\text{F}}$

(ii). If the temperature is \[158^\circ  F\] , then find the temperature in Kelvin.

Ans: Substituting \[y = 158^\circ {\text{ F}}\] in the linear equation \[y = \dfrac{9}{5}(x - 273) + 32\]

$\Rightarrow 158 = \dfrac{9}{5}(x - 273) + 32$

$\Rightarrow 158 = \dfrac{{9(x - 273) + 32 \times 5}}{5}$

$\Rightarrow 158 \times 5 = 9(x - 273) + 160$

$\Rightarrow 790 = 9(x - 273) + 160$

$\Rightarrow 790 - 160 = 9(x - 273)$

$\Rightarrow 9(x - 273) = 630$

$\Rightarrow (x - 273) = \dfrac{{630}}{9} = 70$

$\Rightarrow x - 273 = 70$

$\Rightarrow x = 70 + 273 = {343^ \circ }{\text{K}}$

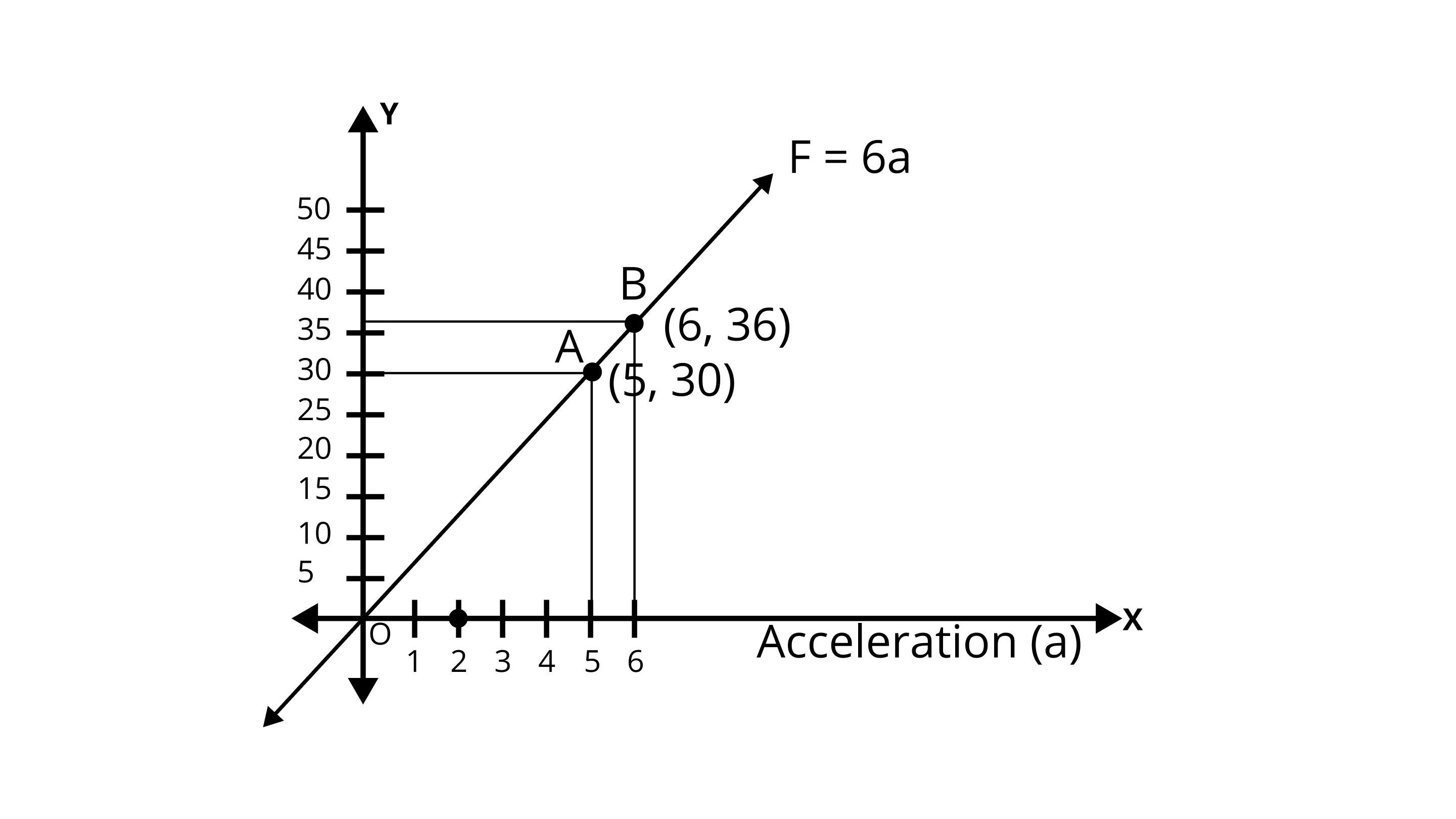
6. The force exerted to pull a cart is directly proportional to the acceleration produced in the body. Express the statement as a linear equation of two variables and draw the graph of the same by taking the constant mass equal to \[6 kg\] . Read from the graph, the force required when the acceleration produced is (i) \[5 m/se{c^2}\] , (ii) \[6 m/se{c^2}\].

Ans: Force is directly proportional to the acceleration produced in the body.

$\Rightarrow F \propto {\text{a}}$

$\Rightarrow F = ma$

$\therefore \;F = 6a$ 

(i). \[a = 5{\text{ m/se}}{{\text{c}}^{\text{2}}}\]

\[F = 6 \times 5 = 30\;{\text{N}}\] 

(ii). \[a = 6{\text{ m/se}}{{\text{c}}^{\text{2}}}\]

\[F = 6 \times 6 = 36\;{\text{N}}\] 

Two points are \[A(5,30)\;{\text{and}}\;B(6,36)\] and plotting a graph

More About NCERT Exemplar for Class 9 Maths - Linear Equations in Two Variables

NCERT Exemplar Solutions for Class 9 Maths Chapter 4 spotlight on developing a comprehension of various concepts of linear equations with two factors. The section covers various topics like the overall form of a linear equation, how to draw a graph of a linear equation, finding the solution of a linear equation, and the condition of the line going through the origin. Vedantu brings you Class 9 Maths NCERT Exemplar Class 9 Maths problems with answers for Chapter 4 where you can undoubtedly set up the concepts in a superior and compelling manner.

Class 9 Maths NCERT Exemplar Chapter 4 has a sum of 4 activities and 42 questions covering various subjects of the whole chapter. The questions of the chapter are planned in a way that they effectively cover serious tests like NTSE alongside CBSE tests. Our topic experts have thus prepared satisfactory answers for your training. Learning the chapter utilizing the NCERT Exemplar will help you in scoring great marks. In this manner, you are encouraged to rehearse NCERT Class 9 Maths Exemplar problems and solutions for Chapter 4 in an appropriate manner to upgrade your insight about the subjects.