NCERT Exemplar for Class 10 Maths Chapter 11 - Areas Related to Circles (Book Solutions)

Multiple Choice Questions

Choose the correct answer from the given four options:

Sample Question 1: If the area of a circle is 154 \[c{m^2}\] , then its perimeter is

(A) 11 cm

(B) 22 cm

(C) 44 cm

(D) 55 cm

Ans: The correct answer is (C).

Given that, the area of a circle is 154 \[c{m^2}\] i.e. \[\pi {r^2} = 154\]

That gives us,

\[ \Rightarrow {r^2} = 154 \times \dfrac{7}{{22}}\]

Or,

\[ \Rightarrow {r^2} = 49\]

Hence,

\[ \Rightarrow r = 7\]

Now the perimeter of this circle is given by,

\[ \Rightarrow 2\pi r = 2 \times \dfrac{{22}}{7} \times 7\]

Hence,

\[ \Rightarrow 2\pi r = 44cm\]

Sample Question 2: If θ is the angle (in degrees) of a sector of a circle of radius r, then area of the sector is

(A) \[\dfrac{{\pi {r^2}\theta }}{{360^\circ }}\]             

(B) \[\dfrac{{\pi {r^2}\theta }}{{180^\circ }}\] 

(C) \[\dfrac{{2\pi r\theta }}{{360^\circ }}\] 

(D) \[\dfrac{{2\pi r\theta }}{{180^\circ }}\]

Ans: The correct answer is (A).

The area of a sector of a circle of radius r and central angle θ is given by the formula,

\[ \Rightarrow A = \dfrac{{\pi {r^2}\theta }}{{360^\circ }}\]

EXERCISE 11.1

Choose the correct answer from the given four options:

1. If the sum of the areas of two circles with radii \[{R_1}\] and \[{R_2}\] in equal to the area of a circle of radius R, then

(a) \[{R_1} + {R_2} = R\]

(b) \[{R_1}^2 + {R_2}^2 = {R^2}\]

(c) \[{R_1} + {R_2} < R\]

(d) \[{R_1}^2 + {R_2}^2 < {R^2}\]

Ans: The correct answer is (b).

According to the question, we have,

\[ \Rightarrow \pi {R_1}^2 + \pi {R_2}^2 = \pi {R^2}\]

Or,

\[ \Rightarrow \pi \left( {{R_1}^2 + {R_2}^2} \right) = \pi {R^2}\]

Hence,

\[ \Rightarrow {R_1}^2 + {R_2}^2 = {R^2}\]

2. If the sum of circumferences of two circles with radii \[{R_1}\] and \[{R_2}\] is equal to the circumference of a circle of radius R, then

(a) \[{R_1} + {R_2} = R\]

(b) \[{R_1} + {R_2} > R\]

(c) \[{R_1} + {R_2} < R\]

(d) Nothing definite can be said about the relation among \[{R_1}\] , \[{R_2}\] and R.

Ans: The correct answer is (a).

According to the question, we have,

\[ \Rightarrow 2\pi {R_1} + 2\pi {R_2} = 2\pi R\]

Or,

\[ \Rightarrow 2\pi \left( {{R_1} + {R_2}} \right) = 2\pi R\]

Hence,

\[ \Rightarrow {R_1} + {R_2} = R\]

3. If the circumference of a circle and the perimeter of a square are equal, then

(a) Area of circle = Area of the square

(b) Area of circle > Area of the square

(c) Area of circle < Area of the square

(d) Nothing definite can be said about the relation between the areas of the circle and square.

Ans: The correct answer is (b).

According to the question, we have,

\[ \Rightarrow 2\pi r = 4a\]

Or,

\[ \Rightarrow a = \dfrac{{\pi r}}{2}\]

Hence, area of square is

\[ \Rightarrow {a^2} = \dfrac{{{\pi ^2}{r^2}}}{{{2^2}}}\]

Or,

\[ \Rightarrow {a^2} = \dfrac{\pi }{4}\left( {\pi {r^2}} \right)\]

Hence,

\[ \Rightarrow {a^2} < \pi {r^2}\]

4. Area of the largest triangle that can be inscribed in a semicircle of radius r units is

(a) \[{r^2}\]square units

(b) \[\dfrac{1}{2}{r^2}\] square units

(c) \[2{r^2}\] square units

(d) \[\sqrt 2 {r^2}\] square units

Ans: The correct answer is (a).

The largest triangle that can be inscribed in a semicircle of radius r units will have its base equal to the diameter and its height equal to the radius of the circle.

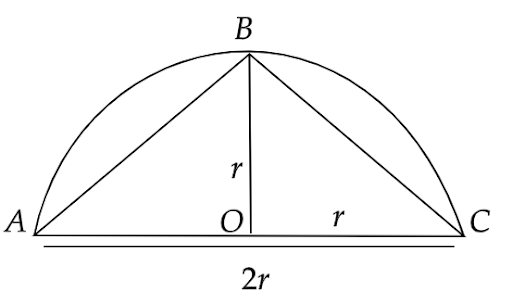
Hence, area of the largest triangle will be,

\[ \Rightarrow \dfrac{1}{2}\left( \text{Base} \right)\left( \text{Height}\right) =  \dfrac{1}{2}\left( \text{Diameter of circle} \right)\left( \text{radius of circle}\right)\]

\[ \Rightarrow \dfrac{1}{2}\left( {2r} \right)\left( r \right) = {r^2}\]

5. If the perimeter of a circle is equal to that of a square, then the ratio of their areas is

(a) 22 : 7

(b) 14 : 11

(c) 7 : 22

(d) 11 : 14

Ans: The correct answer is (b).

According to the question, we have,

\[ \Rightarrow 2\pi r = 4a\]

Or,

\[ \Rightarrow \pi r = 2a\]

Squaring both sides,

\[ \Rightarrow {\pi ^2}{r^2} = 4{a^2}\]

Or,

\[ \Rightarrow \pi {r^2} = \dfrac{4}{\pi }{a^2}\]

Hence,

\[ \Rightarrow \dfrac{{\pi {r^2}}}{{{a^2}}} = \dfrac{4}{\pi } = \dfrac{{4 \times 7}}{{22}}\]

i.e.

\[ \Rightarrow \dfrac{{\pi {r^2}}}{{{a^2}}} = \dfrac{{14}}{{11}}\]

6. It is proposed to build a single circular park equal in area to the sum of areas of two circular parks of diameters 16 m and 12 m in a locality. The radius of the new park would be

(a) 10 m

(b) 15 m

(c) 20 m

(d) 24 m

Ans: The correct answer is (a).

According to the given question, we have \[{d_1} = 12m \Rightarrow {r_1} = 6m\] and \[{d_2} = 16m \Rightarrow {r_2} = 8m\]

\[ \Rightarrow \pi {r_1}^2 + \pi {r_2}^2 = \pi {r^2}\]

That is,

\[ \Rightarrow {r_1}^2 + {r_2}^2 = {r^2}\]

Hence,

\[ \Rightarrow {6^2} + {8^2} = {r^2}\]

i.e.

\[ \Rightarrow r = \sqrt {36 + 64}  = \sqrt {100} \]

Or,

\[ \Rightarrow r = 10m\]

7. Area of the circle that can be inscribed in a square of side 6 cm is

(a) 36π \[c{m^2}\] 

(b) 18π \[c{m^2}\]

(c) 12π \[c{m^2}\]

(d) 9π \[c{m^2}\]

Ans: The correct answer is (d).

The circle that can be inscribed in a square will have its diameter equal to the side of the square.

side = 6cm

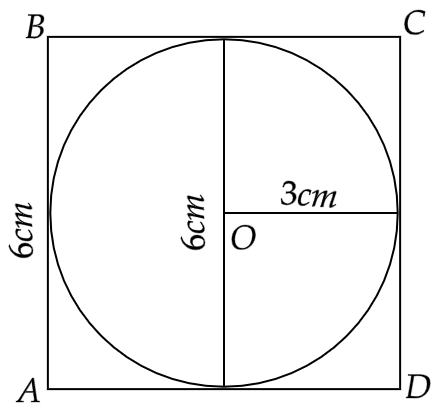
Hence, we have the area of the circle

\[ \Rightarrow \pi {r^2} = \pi {\left( {\dfrac{d}{2}} \right)^2}\]

Hence,

\[ \Rightarrow \pi {r^2} = \pi {\left( {\dfrac{6}{2}} \right)^2} = \pi  \times {3^2} = 9\pi c{m^2}\]

8. The area of the square that can be inscribed in a circle of radius 8 cm is

(a) 256 \[c{m^2}\]

(b) 128 \[c{m^2}\]

(c) \[64\sqrt 2 {\text{ }}c{m^2}\]

(d) 64 \[c{m^2}\]

Ans: The correct answer is (b).

The square that can be inscribed in a circle will have its diagonals equals to the diameter of the circle.

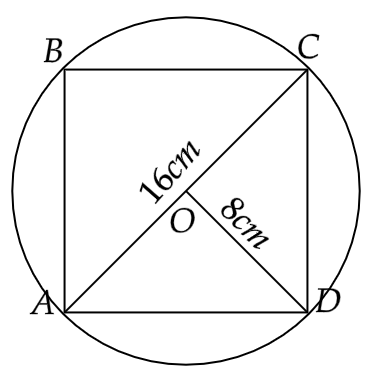
Hence, we have area of the square as

\[ \Rightarrow \dfrac{1}{2}{d_1}{d_2}\]

That gives us,

\[ \Rightarrow \dfrac{1}{2}\left( {2r} \right)\left( {2r} \right)\]

i.e.

\[ \Rightarrow \dfrac{1}{2}\left( {2 \times 8} \right)\left( {2 \times 8} \right)\]

Hence,

\[ \Rightarrow 128c{m^2}\]

9. The radius of a circle whose circumference is equal to the sum of the circumferences of the two circles of diameters 36 cm and 20 cm is

(a) 56 cm

(b) 42 cm

(c) 28 cm

(d) 16 cm

Ans: The correct answer is (c).

Here, we have \[{d_1} = 36cm \Rightarrow {r_1} = 18cm\] and \[{d_2} = 20cm \Rightarrow {r_2} = 10cm\]

Now, according to the question, we have

\[ \Rightarrow 2\pi r = 2\pi {r_1} + 2\pi {r_2}\]

Or,

\[ \Rightarrow r = {r_1} + {r_2}\]

Hence,

\[ \Rightarrow r = 18 + 10 = 28cm\]

10. The diameter of a circle whose area is equal to the sum of the areas of the two circles of radii 24 cm and 7 cm is

(a) 31 cm

(b) 25 cm

(c) 62 cm

(d) 50 cm

Ans: The correct answer is (d).

Here, we have \[{r_1} = 24cm\] and \[{r_2} = 7cm\]

Now, according to the question, we have

\[ \Rightarrow \pi {r^2} = \pi {r_1}^2 + \pi {r_2}^2\]

Or,

\[ \Rightarrow {r^2} = {r_1}^2 + {r_2}^2\]

Hence,

\[ \Rightarrow {r^2} = {\left( {24} \right)^2} + {\left( 7 \right)^2}\]

i.e.,

\[ \Rightarrow {r^2} = {\left( {25} \right)^2}\]

Or,

\[ \Rightarrow r = 25cm\]

Therefore, \[d = 2r = 2\left( {25} \right) = 50cm\]

Short Answer Questions with Reasoning

Sample Question 1 : Is the following statement true? Give reasons for your answer.

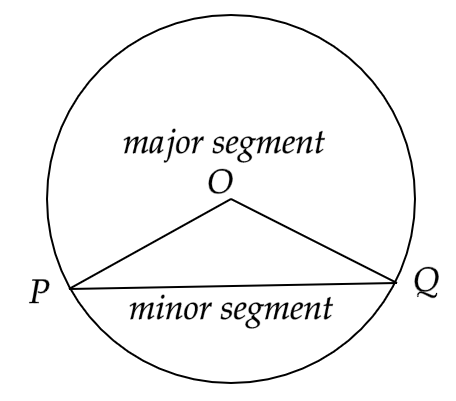
Area of a segment of a circle = area of the corresponding sector – area of the corresponding triangle.

Ans: No, this statement is not true because it is only true in the case of a minor segment.

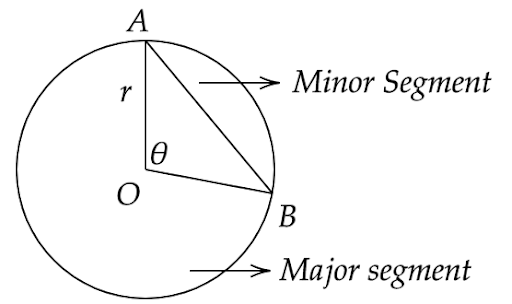
Form the above diagram, we can say that the area of a major is given by,

Area of a major segment of a circle = area of the corresponding sector + area of the corresponding triangle.

Sample Question 2 : In Fig. 11.2, a circle is inscribed in a square of side 5 cm and another circle is circumscribing the square. Is it true to say that area of the outer circle is two times the area of the inner circle? Give reasons for your answer.

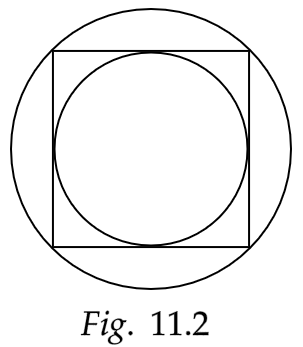
Ans: Given that, the width of the square is \[a = 5cm\]

That is also the diameter of the inner circle, i.e. \[2r = 5cm\]

Hence, the area of the inner circle is,

\[ \Rightarrow \pi {r^2} = \pi {\left( {\dfrac{5}{2}} \right)^2}\]

i.e.

\[ \Rightarrow \pi {r^2} = \dfrac{{25\pi }}{4}\]

Now, the diagonal of the square is the diameter of the outer circle.

The length of the diagonal is \[5\sqrt 2 cm\] i.e. \[2R = 5\sqrt 2 cm\]

So the area of the outer circle is given by,

\[ \Rightarrow \pi {R^2} = \pi {\left( {\dfrac{{5\sqrt 2 }}{2}} \right)^2}\]

That gives us,

\[ \Rightarrow \pi {R^2} = \dfrac{{25\pi }}{2}\]

Therefore comparing these areas we get,

\[ \Rightarrow \pi {R^2} = 2\pi {r^2}\]

Hence, the area of the outer circle is two times the area of the inner circle.

EXERCISE 11.2

1. Is the area of circle inscribed in a square of side a cm, \[\pi {a^2}{\text{ c}}{{\text{m}}^2}\] ? Give reasons for your answer.

Ans: The circle inscribed in a square will have its diameter equal to the width of the square, i.e. \[2r = a \Rightarrow r = \dfrac{a}{2}\]

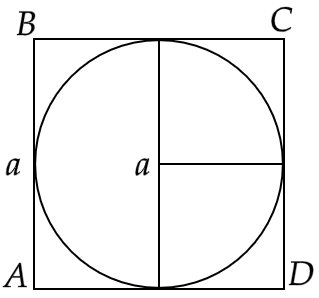
Hence, the area of the circle is,

\[ \Rightarrow \pi {r^2} = \pi {\left( {\dfrac{a}{2}} \right)^2}\]

i.e.

\[ \Rightarrow \pi {r^2} = \dfrac{1}{4}\pi {a^2}\]

Hence, the statement is false.

2. Will it be true to say that the perimeter of the square circumscribing a circle of radius a cm is 8a cm? Give reason for your answer.

Ans: The square circumscribing a circle will have its width equal to the diameter of that circle, i.e. \[l = 2r = 2a\]

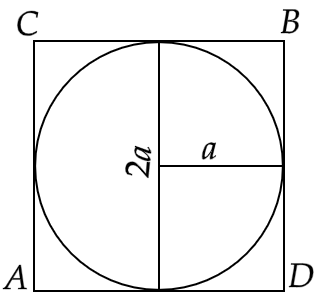
Now, the perimeter of the square will be given by,

\[ \Rightarrow 4l = 4\left( {2a} \right)\]

Hence,

\[ \Rightarrow 4l = 8a\]

Therefore, the statement is true.

3. In the given figure, a square is inscribed in a circle of diameter d and another square is circumscribing the circle. Is the area of the outer square four times the area of the inner square? Give reasons for your answer.

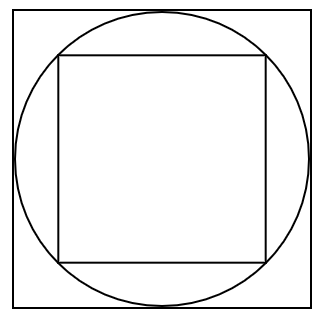
Ans: The smaller square which is inscribed in the circle will have its diagonals equal to the diameter of the circle, i.e. \[{d_1} = {d_2} = d\]

Hence, area of the smaller square is \[\dfrac{1}{2}{d_1}{d_2} = \dfrac{1}{2}d \cdot d = \dfrac{{{d^2}}}{2}\]

Now the larger square which is circumscribing the circle will have its width equal to the diameter of the circle, i.e. \[a = d\]

Hence, area of the larger square is \[{a^2} = {d^2}\]

Therefore, the area of the outer square two times the area of inner square.

So the statement is false.

4. Is it true to say that area of a segment of a circle is less the area of its corresponding sector? Why?

Ans: This statement is only true for minor sectors and segments because in the case of major segments, the area of a major segment is always greater than the area of its corresponding sector.

We can understand it by the figure given below.

Hence, the statement is false.

5. Is it true that the distance travelled by a circular wheel of diameter d cm in one revolution is 2πd cm? Why?

Ans: The distance travelled by circular wheel in one revolution will be equal to its circumference which is given by,

\[ \Rightarrow 2\pi r = 2\pi  \cdot \dfrac{d}{2}\]

Hence,

\[ \Rightarrow \pi d\]

Therefore, the statement is false.

6. In covering a distance of s metres, a circular wheel of radius r m makes \[\dfrac{s}{{2\pi r}}\] revolutions. Is the statement true? Why?

Ans: If the radius of the circular wheel is \[r\] , then its circumference will be \[2\pi r\] .

Now, the number of revolutions to cover a distance of \[s\] metres will be given by,

\[ \Rightarrow n = \dfrac{s}{{2\pi r}}\]

Hence, the statement is true.

7. The numerical value of the area of a circle is greater than the numerical value of its circumference. Is this statement true? Why?

Ans: No, this statement is not true because the numerical values of the area of a circle can be all lesser, equal or greater than the numerical value of its circumference, depending on its radius.

For example, if we have the numerical value of area equal to that of the circumference,

Then we have

\[ \Rightarrow \pi {r^2} = 2\pi r\]

i.e.

\[ \Rightarrow {r^2} = 2r\]

Hence,

\[ \Rightarrow r = 2\]

Now if we take \[r < 2\] then the area will be less than its circumference

Also, if we take \[r > 2\] then the area will be greater than its circumference.

Hence, the given statement is false.

8. If the length of an arc of a circle of radius r is equal to that of an arc of a circle of radius 2r, then the angle of the corresponding sector of the first circle is double the angle of the corresponding sector of other circle. Is this statement false? Why?

Ans: According to the given question, we have two circles of radii r and 2r.

Now if their arcs are equal, then we have

\[ \Rightarrow \dfrac{{2\pi r{\theta _1}}}{{360^\circ }} = \dfrac{{2\pi \left( {2r} \right){\theta _2}}}{{360^\circ }}\]

That gives us,

\[ \Rightarrow {\theta _1} = 2{\theta _2}\]

Hence, the angle of the sector of the first circle is double than that of the second circle.

Therefore, the given statement is true.

9. The area of two sectors of two different circles with equal corresponding arc length are equal. Is this statement true? Why?

Ans: According to the question, we have two different circles with equal corresponding arc lengths, i.e.

\[ \Rightarrow \dfrac{{2\pi {r_1}{\theta _1}}}{{360^\circ }} = \dfrac{{2\pi {r_2}{\theta _2}}}{{360^\circ }}\]

That gives us,

\[ \Rightarrow \dfrac{{\pi {r_1}{\theta _1}}}{{360^\circ }} = \dfrac{{\pi {r_2}{\theta _2}}}{{360^\circ }}\]

Now the area of their sectors will be equal if and only if their radii are equal, i.e. \[{r_1} = {r_2}\]

Hence, if \[{r_1} = {r_2}\] then we have

\[ \Rightarrow \dfrac{{\pi {r_1}{\theta _1}}}{{360^\circ }} \cdot {r_1} = \dfrac{{\pi {r_2}{\theta _2}}}{{360^\circ }} \cdot {r_2}\]

Or,

\[ \Rightarrow \dfrac{{\pi {r_1}^2{\theta _1}}}{{360^\circ }} = \dfrac{{\pi {r_2}^2{\theta _2}}}{{360^\circ }}\]

Therefore, the given statement is not true.

10. The areas of two sectors of two different circles are equal. Is it necessary that their corresponding arc lengths are equal? Why?

Ans: According to the question, if the areas of two sectors of two different circles are equal,

Then, we have

\[ \Rightarrow \dfrac{{\pi {r_1}^2{\theta _1}}}{{360^\circ }} = \dfrac{{\pi {r_2}^2{\theta _2}}}{{360^\circ }}\]

That gives us,

\[ \Rightarrow \dfrac{{2\pi {r_1}{\theta _1}}}{{360^\circ }} \cdot {r_1} = \dfrac{{2\pi {r_2}{\theta _2}}}{{360^\circ }} \cdot {r_2}\]

The above depends on both radius and angle subtended at the center and arc length also depends on radius and angle. Therefore, it is not necessary that the corresponding arc lengths are equal. It is possible only if corresponding angles are equal because then, the corresponding radii will be equal and hence the arc lengths will be equal). Therefore, the given statement is not true.

11. Is the area of the largest circle that can be drawn inside a rectangle of length a cm and breadth b cm (a > b) is \[\pi {b^2}{\text{ c}}{{\text{m}}^2}\] ? Why?

Ans: The largest circle that can be drawn inside a rectangle will have its diameter equal to the width of the rectangle.

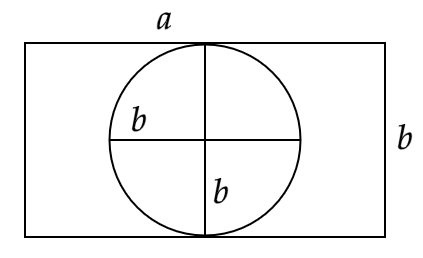
That gives,

\[ \Rightarrow d = 2r = b\]

i.e. 

\[ \Rightarrow r = \dfrac{b}{2}\]

Hence, the area of this circle will be given by,

\[ \Rightarrow \pi {r^2} = \pi {\left( {\dfrac{b}{2}} \right)^2}\]

i.e.

\[ \Rightarrow \pi {r^2} = \dfrac{1}{4}\pi {b^2}\]

Hence, the given statement is false.

12. Circumferences of two circles are equal. Is it necessary that their areas be equal? Why?

Ans: If the circumferences of two circles are equal, then we have

\[ \Rightarrow 2\pi {r_1} = 2\pi {r_2}\]

That gives us,

\[ \Rightarrow {r_1} = {r_2}\]

Hence,

\[ \Rightarrow \pi {r_1}^2 = \pi {r_2}^2\]

Therefore, the given statement is true.

13. Areas of the two circles are equal. Is it necessary that their circumferences are equal? Why?

Ans: If the areas of the two circles are equal, then we have

\[ \Rightarrow \pi {r_1}^2 = \pi {r_2}^2\]

Or,

\[ \Rightarrow {r_1}^2 = {r_2}^2\]

That gives us,

\[ \Rightarrow {r_1} = {r_2}\]

Hence,

\[ \Rightarrow 2\pi {r_1} = 2\pi {r_2}\]

Therefore, the given statement is true.

14. Is it true to say that the area of a square inscribed in a circle of diameter p cm is \[{p^2}c{m^2}\] ? Why?

Ans: The square inscribed in a circle will have both its diagonals equal to the length of the diameter of the circle, i.e. \[{d_1} = {d_2} = d\]

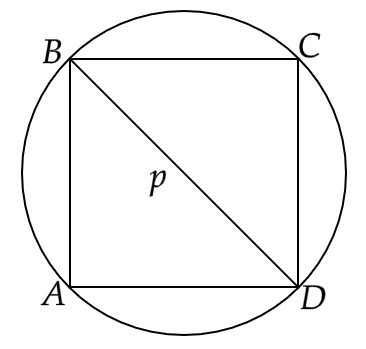
Given that \[d = p{\text{ cm}}\]

Hence \[{d_1} = {d_2} = d = p{\text{ cm}}\]

Now, the area of the square will be given by,

\[ \Rightarrow \dfrac{1}{2}{d_1}{d_2}\]

That is,

\[ \Rightarrow \dfrac{1}{2}p \cdot p\]

Hence,

\[ \Rightarrow \dfrac{1}{2}{p^2}{\text{ c}}{{\text{m}}^2}\]

Therefore, the given statement is false.

Short Answer Questions

Sample Question 1: Find the diameter of the circle whose area is equal to the sum of the areas of the two circles of diameters 20 cm and 48 cm.

Ans: Given that, the area of a circle is equal to the sum of the areas of the two circles of diameters 20 cm and 48 cm i.e. of radii 10cm and 24cm respectively.

Hence, we have

\[ \Rightarrow \pi {r^2} = \pi {\left( {10} \right)^2} + \pi {\left( {24} \right)^2}\]

That gives us,

\[ \Rightarrow {r^2} = 100 + 576\]

Or,

\[ \Rightarrow r = \sqrt {676} \]

Hence,

\[ \Rightarrow r = 26cm\]

Therefore, the diameter of this circle is \[2r = 52cm\] .

Sample Question 2: Find the area of a sector of circle of radius 21 cm and central angle 120°.

Ans: Given that, a sector of a circle of radius 21cm and central angle 120°.

Hence, the area of this sector will be given by,

\[ \Rightarrow \dfrac{{\pi {r^2}\theta }}{{360^\circ }} = \pi {\left( {21} \right)^2} \cdot \dfrac{{120^\circ }}{{360^\circ }}\]

That gives us,

\[ \Rightarrow \dfrac{{\pi {r^2}\theta }}{{360^\circ }} = \dfrac{{22}}{7} \times 21 \times 21 \times \dfrac{1}{3}\]

Therefore,

\[ \Rightarrow \dfrac{{\pi {r^2}\theta }}{{360^\circ }} = 462c{m^2}\]

Sample Question 3: In Fig 11.4, a circle of radius 7.5 cm is inscribed in a square. Find the area of the shaded region (Use π = 3.14)

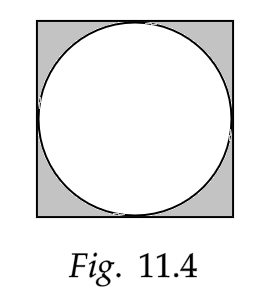
Ans: Given that, the radius of the circle is \[r = 7.5cm\]

So the area of this circle is given by,

\[ \Rightarrow \pi {r^2} = \pi {\left( {\dfrac{{15}}{2}} \right)^2}\]

That is,

\[ \Rightarrow \pi {r^2} = 3.14 \times \dfrac{{225}}{4}\]

Hence,

\[ \Rightarrow \pi {r^2} = 176.625c{m^2}\]

Now, the width of the square is equal to the diameter of the circle, i.e. \[a = 15cm\]

Hence, the area of the square is,

\[ \Rightarrow {a^2} = 15 \times 15\]

That is,

\[ \Rightarrow {a^2} = 225c{m^2}\]

Therefore, now the area of the shaded region can be given by,

\[ \Rightarrow {a^2} - \pi {r^2} = 225 - 176.625\]

That gives us,

\[ \Rightarrow {a^2} - \pi {r^2} = 48.375c{m^2}\]

Sample Question 4: Area of a sector of a circle of radius 36 cm is 54π \[c{m^2}\] . Find the length of the corresponding arc of the sector.

Ans: Given that, a circle of radius \[r = 36cm\] and a sector of area \[54\pi c{m^2}\] .

That can be written as,

\[ \Rightarrow \dfrac{{\pi {r^2}\theta }}{{360^\circ }} = 54\pi c{m^2}\]

Dividing both sides by \[r = 36cm\] , we get

\[ \Rightarrow \dfrac{{\pi r\theta }}{{360^\circ }} = \dfrac{{54\pi }}{r}\]

Multiplying both sides by 2, we get

\[ \Rightarrow \dfrac{{2\pi r\theta }}{{360^\circ }} = 2 \times \dfrac{{54\pi }}{{\left( {36} \right)}}\]

Now, on solving this equation, we have

\[ \Rightarrow \dfrac{{2\pi r\theta }}{{360^\circ }} = 3\pi \]

Here, LHS represents the length of the corresponding arc of the sector.

Hence, the length of the corresponding arc of the sector is \[3\pi cm\] .

EXERCISE 11.3

1. Find the radius of a circle whose circumference is equal to the sum of the circumference of two circles of radii 15 cm and 18 cm.

Ans: Given that, the circumference of a circle is equal to the sum of the circumference of two other circles of radii 15 cm and 18 cm.

Therefore, we have

\[ \Rightarrow 2\pi r = 2\pi {r_1} + 2\pi {r_2}\]

That is,

\[ \Rightarrow r = {r_1} + {r_2}\]

i.e.

\[ \Rightarrow r = 15 + 18\]

Hence,

\[ \Rightarrow r = 33cm\]

2. In the given figure, a square of diagonal 8 cm is inscribed in a circle. Find the area of the shaded region.

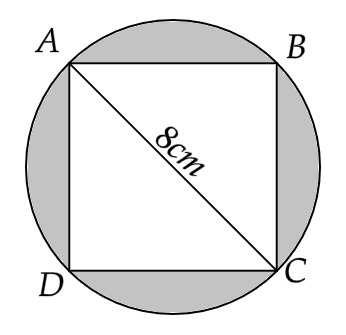
Ans: In the given figure, the diameter of the circle is equal to the diagonal of the square.

Hence, we have \[d = 2r = 8cm\] i.e. \[r = 4cm\]

Area of the circle,

\[ \Rightarrow \pi {r^2} = \pi {\left( 4 \right)^2}\]

Or,

\[ \Rightarrow \pi {r^2} = 16\pi c{m^2}\]

Now, side of the square is \[a = \dfrac{d}{{\sqrt 2 }} = \dfrac{8}{{\sqrt 2 }}\]

Area of square,

\[ \Rightarrow {a^2} = {\left( {\dfrac{8}{{\sqrt 2 }}} \right)^2}\]

Or,

\[ \Rightarrow {a^2} = \dfrac{{64}}{2}\]

i.e.

\[ \Rightarrow {a^2} = 32c{m^2}\]

Now the area of the shaded region will be given by the difference of these two areas.

That is,

\[ \Rightarrow \pi {r^2} - {a^2} = 16\pi  - 32\]

That is,

\[ \Rightarrow \pi {r^2} - {a^2} = 16\left( {\pi  - 2} \right)\]

Or,

\[ \Rightarrow \pi {r^2} - {a^2} = 16\left( {3.14 - 2} \right) = 16\left( {1.14} \right)\]

i.e.

\[ \Rightarrow \pi {r^2} - {a^2} = 18.286c{m^2}\]

3. Find the area of a sector of a circle of radius 28 cm and central angle 45°.

Ans: The area of a sector of a circle is given by the formula \[\dfrac{{\pi {r^2}\theta }}{{360^\circ }}\] where \[\theta \] is the central angle.

Therefore, when \[r = 28cm\] and \[\theta  = 45^\circ \]

Then the area of sector is,

\[ \Rightarrow \dfrac{{\pi {r^2}\theta }}{{360^\circ }} = \pi {\left( {28} \right)^2}\dfrac{{45^\circ }}{{360^\circ }}\]

That gives us,

\[ \Rightarrow \dfrac{{\pi {r^2}\theta }}{{360^\circ }} = \dfrac{{22}}{7} \times 28 \times 28 \times \dfrac{1}{8}\]

Or,

\[ \Rightarrow \dfrac{{\pi {r^2}\theta }}{{360^\circ }} = 22 \times 14\]

Hence,

\[ \Rightarrow \dfrac{{\pi {r^2}\theta }}{{360^\circ }} = 308c{m^2}\]

4. The wheel of a motorcycle is of radius 35 cm. How many revolutions per minute must the wheel make so as to keep a speed of 66 km/hr?

Ans: Given that, the radius of the wheel of a motorcycle is \[r = 35cm = 0.35m\]

The required speed of motorcycle is \[v = 66km/h = 66 \times \dfrac{5}{{18}} = \dfrac{{55}}{3}m/s\]

Here the revolution is required per minute, i.e. \[t = 1\min  = 60\sec \]

Now since we know that speed is the distance covered per unit time,

Hence, we have

\[ \Rightarrow v = \dfrac{{2\pi rn}}{t}\]

Where n is the number of revolutions per minute.

Now, that can be written as

\[ \Rightarrow n = \dfrac{{vt}}{{2\pi r}}\]

That gives us,

\[ \Rightarrow n = \dfrac{{55 \times 60}}{{2 \times 3 \times \pi  \times 0.35}}\]

Or,

\[ \Rightarrow n = \dfrac{{55 \times 10 \times 7 \times 100}}{{22 \times 35}}\]

That is,

\[ \Rightarrow n = 5 \times 100\]

Hence,

\[ \Rightarrow n = 500\]

Therefore, the wheel must make 500 revolutions per minute so as to keep a speed of 66 km/hr.

5. A cow is tied with a rope of length 14 m at the corner of a rectangular field of dimensions 20 m × 16 m. Find the area of the field in which the cow can graze.

Ans: If the cow is tied at a corner of a rectangular field, then she can graze an area equal to that of a sector of a circle of radius \[r = 14m\] and \[\theta  = 90^\circ \] since the corner of a rectangle is at right angle.

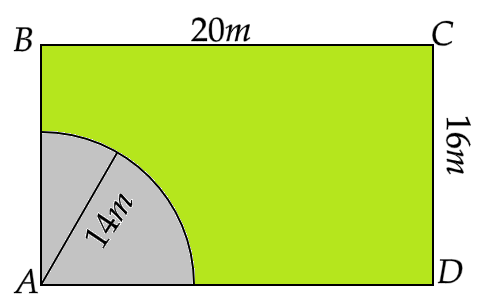
Therefore, the area of field in which the cow can graze is given by,

\[ \Rightarrow \dfrac{{\pi {r^2}\theta }}{{360^\circ }} = \pi {\left( {14} \right)^2} \cdot \dfrac{{90^\circ }}{{360^\circ }}\]

That is,

\[ \Rightarrow \dfrac{{\pi {r^2}\theta }}{{360^\circ }} = \dfrac{{22}}{7} \times 14 \times 14 \times \dfrac{1}{4}\]

Or,

\[ \Rightarrow \dfrac{{\pi {r^2}\theta }}{{360^\circ }} = 22 \times 7\]

Hence,

\[ \Rightarrow \dfrac{{\pi {r^2}\theta }}{{360^\circ }} = 154{m^2}\]

6. Find the area of flower bed (with semi–circular ends) shown in figure.

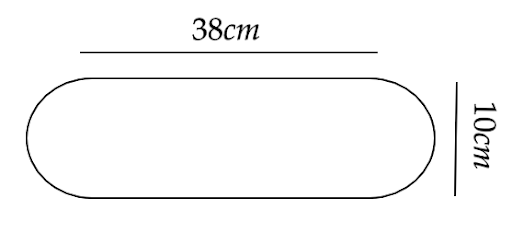
Ans: In order to find the area of the flower bed, we can find the area of the two semi-circular ends and the rectangle in the middle separately.

The diameter of the semicircle is given as \[d = 10cm\] hence the radius is \[r = 5cm\]

Now the area of two semicircles will be given by

\[ \Rightarrow 2 \times \dfrac{{\pi {r^2}}}{2} = 2 \times \dfrac{\pi }{2}{\left( 5 \right)^2}\]

That gives us,

\[ \Rightarrow 2 \times \dfrac{{\pi {r^2}}}{2} = 25\pi \]

That is,

\[ \Rightarrow 2 \times \dfrac{{\pi {r^2}}}{2} = 25 \times 3.14 = 78.54c{m^2}\]

For the area of the rectangular region, we have \[l = 38cm\] and \[b = 10cm\]

Hence,

\[l \times b = 38 \times 10\]

That is,

\[l \times b = 380c{m^2}\]

Therefore, the area of the flower bed is,

\[ \Rightarrow 380 + 78.54\]

Hence,

\[ \Rightarrow 458.54c{m^2}\]

7. In the given figure, AB is diameter of circle, AC = 6 and BC = 8 cm. Find the area of the shaded region. (π = 3.14).

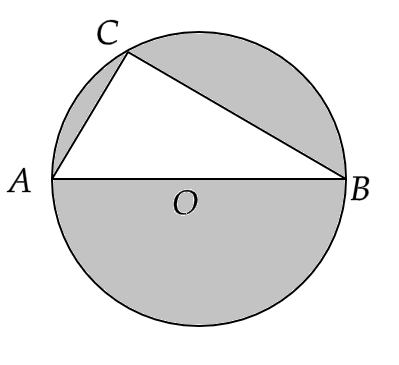
Ans: From the figure, we have a right angled triangle ABC inscribed in the circle with centre O.

The side AB of triangle ABC is the diameter of the circle.

Now in triangle ABC, by Pythagoras theorem,

We have

\[ \Rightarrow A{B^2} = A{C^2} + B{C^2}\]

That gives us,

\[ \Rightarrow A{B^2} = {\left( 6 \right)^2} + {\left( 8 \right)^2}\]

Or,

\[ \Rightarrow A{B^2} = 36 + 64 = 100\]

Hence,

\[ \Rightarrow AB = \sqrt {100}  = 10cm\]

So the diameter of the circle is 10cm, i.e. its radius is \[r = 5cm\]

Now area of triangle ABC will be given by,

\[ \Rightarrow \dfrac{1}{2}bh = \dfrac{1}{2} \times 6 \times 8\]

Hence,

\[ \Rightarrow \dfrac{1}{2}bh = 24c{m^2}\]

Also the area of the circle will be given by,

\[ \Rightarrow \pi {r^2} = \pi  \times {\left( 5 \right)^2}\]

Hence,

\[ \Rightarrow \pi {r^2} = 25\pi {cm^2}\]

Therefore, the area of the shaded region will be given by the difference of these two areas,

Hence,

\[ \Rightarrow \pi {r^2} - \dfrac{1}{2}bh = 25\pi  - 24{cm^2}\]

That is,

\[ \Rightarrow \pi {r^2} - \dfrac{1}{2}bh = 78.54 - 24{cm^2}\]

Therefore,

\[ \Rightarrow \pi {r^2} - \dfrac{1}{2}bh = 54.54{cm^2}\]

8. Find the area of the shaded field shown in the given figure.

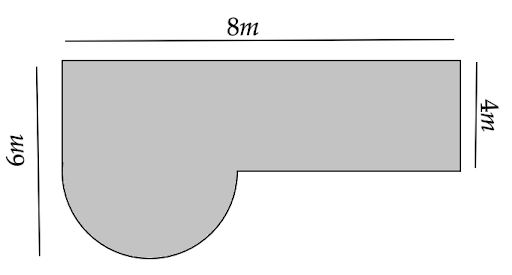
Ans: In order to find the area of the shaded field, we can find the area of the semi-circular end and the rectangular region separately.

For the semicircular region, we have its radius equal to \[r = 6 - 4 = 2m\]

Hence, its area is \[\dfrac{1}{2}\pi {r^2}\]

That gives,

\[ \Rightarrow \dfrac{1}{2}\pi {r^2} = \dfrac{1}{2}\pi {\left( 2 \right)^2}\]

i.e.

\[ \Rightarrow \dfrac{1}{2}\pi {r^2} = 2\pi {\text{ }}{m^2}\]

Now, for the rectangular region, we have \[l = 8m\] and \[b = 4m\]

Hence, its area is

\[ \Rightarrow l \times b = 8 \times 4\]

i.e.

\[ \Rightarrow l \times b = 32{\text{ }}{{\text{m}}^2}\]

Therefore, the area of the shaded region is

\[ \Rightarrow \left( {l \times b} \right) + \dfrac{1}{2}\pi {r^2} = 32{\text{ }} + 2\pi \]

That is,

\[ \Rightarrow \left( {l \times b} \right) + \dfrac{1}{2}\pi {r^2} = 32{\text{ }} + 6.28\]

Or,

\[ \Rightarrow \left( {l \times b} \right) + \dfrac{1}{2}\pi {r^2} = 38.28{\text{ }}{{\text{m}}^2}\]

9. Find the area of the shaded region in the given figure.

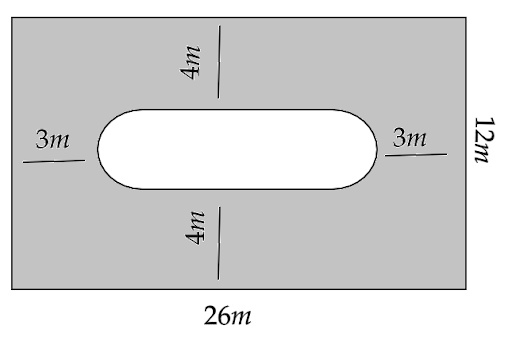
Ans: First we have to find the area of the unshaded region.

Here, the diameter of the two semicircular ends will be given by \[d = 12 - 4 - 4 = 4m\]

Hence the area of the two semicircular ends is

\[ \Rightarrow 2 \times \dfrac{1}{2} \times \pi {r^2} = \pi {\left( {\dfrac{d}{2}} \right)^2}\]

Or,

\[ \Rightarrow 2 \times \dfrac{1}{2} \times \pi {r^2} = \pi {\left( {\dfrac{4}{2}} \right)^2}\]

That is,

\[ \Rightarrow 2 \times \dfrac{1}{2} \times \pi {r^2} = 4\pi \]

i.e.

\[ \Rightarrow 2 \times \dfrac{1}{2} \times \pi {r^2} = 12.56{\text{ }}{{\text{m}}^2}\]

Now, for the unshaded rectangular region we have \[l = 26 - 3 - 3 - 2r = 20 - 4 = 16m\] and \[b = d = 4m\]

Hence, the area of the unshaded rectangular region is

\[ \Rightarrow l \times b = 16 \times 4\]

That is,

\[ \Rightarrow l \times b = 64{\text{ }}{{\text{m}}^2}\]

Therefore, the total area of unshaded region is \[64 + 12.56 = 76.56{\text{ }}{{\text{m}}^2}\]

Now, the area of the whole region is a rectangle of \[l = 26m\] and \[b = 12m\]

Hence, total area is

\[ \Rightarrow l \times b = 26 \times 12\]

That is,

\[ \Rightarrow l \times b = 312{\text{ }}{{\text{m}}^2}\]

Therefore, the required area of the shaded region is given by the difference of the total area and the unshaded area.

Hence, the shaded area is

\[ \Rightarrow 312 - 76.56\]

That is,

\[ \Rightarrow 235.44{\text{ }}{{\text{m}}^2}\]

10. Find the area of the minor segment of circle of radius 14 cm, when the angle of corresponding sector is 60°.

Ans: The area of the segment AB is given by the difference of areas of the corresponding sector and the triangle AOB as shown in the figure below.

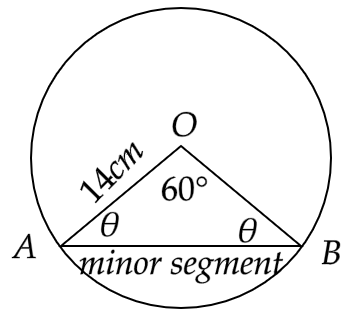
Here, the area of the sector will be given by

\[ \Rightarrow \dfrac{{\pi {r^2}\theta }}{{360^\circ }} = \pi {\left( {14} \right)^2}\dfrac{{60^\circ }}{{360^\circ }}\]

That is,

\[ \Rightarrow \dfrac{{\pi {r^2}\theta }}{{360^\circ }} = 22 \times 2 \times 14 \times \dfrac{1}{6}\]

i.e.

\[ \Rightarrow \dfrac{{\pi {r^2}\theta }}{{360^\circ }} = \dfrac{{22 \times 14}}{3}{\text{ c}}{{\text{m}}^2}\]

Now in triangle AOB, we have \[AO = OB = 14cm\] and \[\angle AOB = 60^\circ \]

Hence,

\[ \Rightarrow \angle OAB = \angle OBA = \dfrac{{\left( {180 - 60} \right)}}{2}\]

Or,

\[ \Rightarrow \angle OAB = \angle OBA = \angle {\rm A}{\rm O}{\rm B} = 60^\circ \]

Therefore, triangle AOB is an equilateral triangle,

Now area of triangle AOB will be given by,

\[ \Rightarrow \dfrac{{\sqrt 3 }}{4}{a^2} = \dfrac{{\sqrt 3 }}{4} \times 14 \times 14\]

That is,

\[ \Rightarrow \dfrac{{\sqrt 3 }}{4}{a^2} = 49\sqrt 3 {\text{ }}{{\text{cm}}^2}\]

Now the area of the segment AB will be given by

\[ \Rightarrow \dfrac{{\pi {r^2}\theta }}{{360^\circ }} - \dfrac{{\sqrt 3 }}{4}{a^2} = \dfrac{{22 \times 14}}{3}{\text{  - }}49\sqrt 3 {\text{ }}\]

That gives  us,

\[ \Rightarrow \dfrac{{\pi {r^2}\theta }}{{360^\circ }} - \dfrac{{\sqrt 3 }}{4}{a^2} = 102.666 - 84.870\]

i.e.

\[ \Rightarrow \dfrac{{\pi {r^2}\theta }}{{360^\circ }} - \dfrac{{\sqrt 3 }}{4}{a^2} = 17.796{\text{ c}}{{\text{m}}^2}\]

11. Find the area of the shaded region in figure, where arcs drawn with centres, A, B, C and D intersect in pairs at mid points P, Q, R and S of the side AB, BC, CD and DA respectively of a square ABCD. (Use π = 3.14)

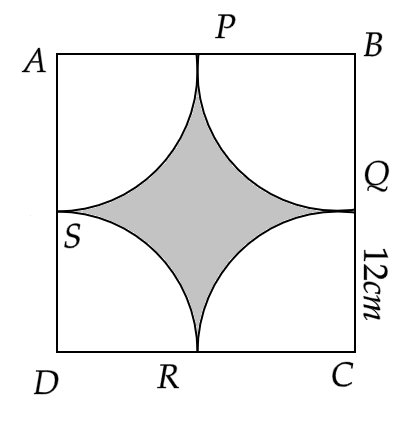
Ans: Since the width of the square is given as \[a = 12cm\]

Hence, the area of the square is,

\[ \Rightarrow {a^2} = {\left( {12} \right)^2} = 144c{m^2}\]

Now, we have the radius of each part of the circle equal to the half of the width of the square,

That is \[r = \dfrac{a}{2} = \dfrac{{12}}{2} = 6cm\]

Now the total area of four \[\dfrac{1}{4}th\] parts of the circle will be given by

\[ \Rightarrow 4 \times \dfrac{1}{4} \times \pi {r^2} = \pi {\left( 6 \right)^2}\]

That is,

\[ \Rightarrow 4 \times \dfrac{1}{4} \times \pi {r^2} = 36\pi \]

Or,

\[ \Rightarrow 4 \times \dfrac{1}{4} \times \pi {r^2} = 36 \times 3.14 = 113.04{\text{ c}}{{\text{m}}^2}\]

Now, the area of the shaded region will be given by the difference of these two areas.

Hence,

\[ \Rightarrow 144 - 113.04 = 30.96c{m^2}\]

12. In the given figure, arcs are drawn by taking vertices A, B and C of an equilateral triangle of side 10 cm to intersect the sides BC, AB and CA at their respective mid points D, E and F respectively. Find the area of the shaded region. (Use π = 3.14)

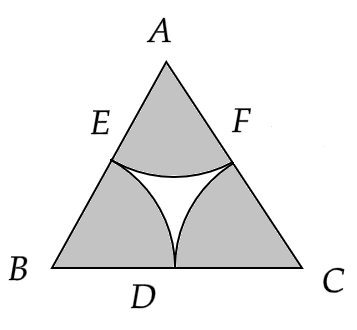
Ans: The shaded region in the given figure is the same as three equal sectors of a circle.

Now the radius of each sector will be half of the length of the equilateral triangle.

That is, \[r = \dfrac{{10}}{2} = 5cm\]

Hence the area of the shaded region will be given by \[3 \times \dfrac{{\pi {r^2}\theta }}{{360^\circ }}\] where \[\theta  = 60^\circ \] since ABC is an equilateral triangle.

Therefore, we have

\[ \Rightarrow 3 \times \dfrac{{\pi {r^2}\theta }}{{360^\circ }} = 3 \times \pi {\left( 5 \right)^2} \times \dfrac{{60^\circ }}{{360^\circ }}\]

That is,

\[ \Rightarrow 3 \times \dfrac{{\pi {r^2}\theta }}{{360^\circ }} = 3 \times 25\pi  \times \dfrac{1}{6}\]

Or,

\[ \Rightarrow 3 \times \dfrac{{\pi {r^2}\theta }}{{360^\circ }} = \dfrac{{25 \times 3.14}}{2}\]

Hence,

\[ \Rightarrow 3 \times \dfrac{{\pi {r^2}\theta }}{{360^\circ }} = 39.25c{m^2}\]

13. In the given figure, arcs have been drawn with radii 14 cm each and with centre P, Q and R. Find the area of the shaded region.

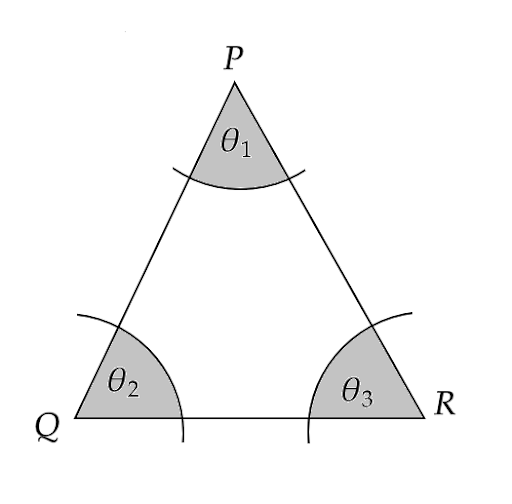
Ans: Given that, there are three sectors of the same radii and angle \[{\theta _1},{\theta _2},{\theta _3}\] respectively.

Now, by the angle sum property of a triangle we have \[{\theta _1} + {\theta _2} + {\theta _3} = 180^\circ \]

Hence, the area of the shaded region will be given by the sum of areas of three sectors respectively.

That is given by,

\[ \Rightarrow \dfrac{{\pi {r^2}{\theta _1}}}{{360^\circ }} + \dfrac{{\pi {r^2}{\theta _2}}}{{360^\circ }} + \dfrac{{\pi {r^2}{\theta _3}}}{{360^\circ }}\]

Or,

\[ \Rightarrow \dfrac{{\pi {r^2}}}{{360^\circ }}\left( {{\theta _1} + {\theta _2} + {\theta _3}} \right)\]

Since \[r = 14cm\] is given and \[{\theta _1} + {\theta _2} + {\theta _3} = 180^\circ \] that gives us,

\[ \Rightarrow \pi {\left( {14} \right)^2} \cdot \dfrac{{180^\circ }}{{360^\circ }}\]

That is,

\[ \Rightarrow \dfrac{{22}}{7} \times 14 \times 14 \times \dfrac{1}{2}\]

i.e.

\[ \Rightarrow 22 \times 14\]

Hence,

\[ \Rightarrow 308c{m^2}\]

14. A circular park is surrounded by a road 21 m wide. If the radius of the park is 105 m, then find the area of the road.

Ans: Given that, the radius of the park is \[{r_1} = 105m\]

Also, the park is surrounded by a road 21 m wide.

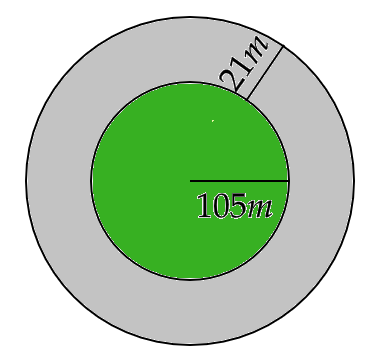
Hence, the radius of the park including the road is \[{r_2} = {r_1} + 21 = 105 + 21 = 126m\]

Now the area of the road will be given by the difference of area of park including the road and the area of only the park.

Hence, we have the area of the road equal to

\[ \Rightarrow \pi {r_2}^2 - \pi {r_1}^2\]

That gives us,

\[ \Rightarrow \pi \left( {{r_2}^2 - {r_1}^2} \right)\]

Or,

\[ \Rightarrow \pi \left( {{r_2} + {r_1}} \right)\left( {{r_2} - {r_1}} \right)\]

Hence,

\[ \Rightarrow \pi \left( {126 + 105} \right)\left( {126 - 105} \right)\]

i.e.

\[ \Rightarrow \dfrac{{22}}{7} \times \left( {231} \right)\left( {21} \right)\]

That is,

\[ \Rightarrow 22 \times 33 \times 21\]

Hence,

\[ \Rightarrow 15246{m^2}\]

15. In the given figure, arcs have been drawn of radius 21 cm each with vertices A, B, C and D of quadrilateral ABCD as centre. Find the area of the shaded region.

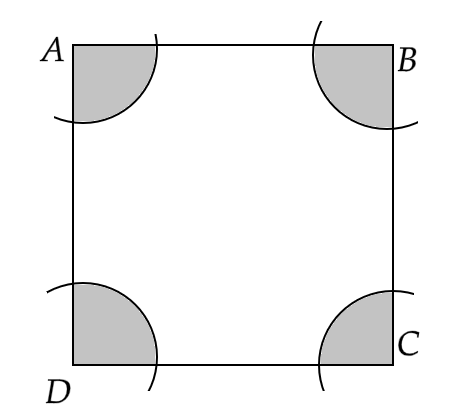
Ans: Given that, there are four sectors of the same radii \[r = 21cm\] and angles \[{\theta _1},{\theta _2},{\theta _3}{\text{ and }}{\theta _4}\] respectively.

Now, by the angle sum property of a quadrilateral we have \[{\theta _1} + {\theta _2} + {\theta _3} + {\theta _4} = 360^\circ \]

Hence, the area of the shaded region will be given by the sum of areas of the four sectors respectively.

That is given by,

\[ \Rightarrow \dfrac{{\pi {r^2}{\theta _1}}}{{360^\circ }} + \dfrac{{\pi {r^2}{\theta _2}}}{{360^\circ }} + \dfrac{{\pi {r^2}{\theta _3}}}{{360^\circ }} + \dfrac{{\pi {r^2}{\theta _4}}}{{360^\circ }}\]

Or,

\[ \Rightarrow \pi {r^2} \cdot \dfrac{{\left( {{\theta _1} + {\theta _2} + {\theta _3} + {\theta _4}} \right)}}{{360^\circ }}\]

That gives us,

\[ \Rightarrow \pi {\left( {21} \right)^2} \cdot \dfrac{{360^\circ }}{{360^\circ }}\]

That is,

\[ \Rightarrow \dfrac{{22}}{7} \times 21 \times 21 \times 1\]

Hence,

\[ \Rightarrow 22 \times 3 \times 21\]

i.e.

\[ \Rightarrow 1386c{m^{2}}\]

16. A piece of wire 20 cm long is bent into the form of an arc of a circle subtending an angle of 60° at its centre. Find the radius of the circle.

Ans: Given that, the length of wire is \[l = 20cm\]

Now if the wire is bent into the form of an arc of a circle subtending an angle of \[\theta  = 60^\circ \] at its centre then we have,

\[ \Rightarrow \dfrac{{2\pi r\theta }}{{360^\circ }} = l\]

That gives us,

\[ \Rightarrow r = \dfrac{l}{{2\pi }} \cdot \dfrac{{360^\circ }}{\theta }\]

Hence,

\[ \Rightarrow r = \dfrac{{20}}{{2\pi }} \cdot \dfrac{{360^\circ }}{{60^\circ }}\]

That is,

\[ \Rightarrow r = \dfrac{{20}}{{2\pi }} \times 6\]

Or,

\[ \Rightarrow r = 20 \times 3 \times \dfrac{7}{{22}}\]

i.e.

\[ \Rightarrow r = \dfrac{{210}}{{11}}\]

Hence,

\[ \Rightarrow r = 19.09cm\]

Long Answer Questions:

Sample Question 1 : A chord of a circle of radius 20 cm subtends an angle of 90° at the centre. Find the area of the corresponding major segment of the circle. (Use π = 3.14).

Ans: Given that, a circle of radius \[r = 20cm\]

Let a chord AB subtending a right angle at the centre O.

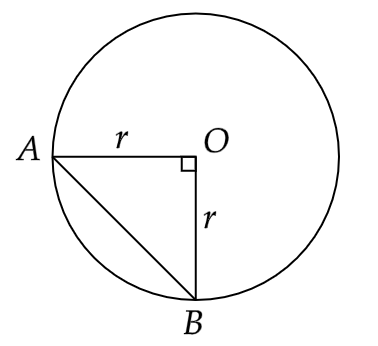
Now the area of the right triangle AOB will be given by,

\[ \Rightarrow \dfrac{1}{2}\left( {r \times r} \right) = \dfrac{1}{2} \times 20 \times 20\]

That gives us,

\[ \Rightarrow \dfrac{1}{2}{r^2} = 200c{m^2}\]

Also, the area of the major sector will be given by,

\[ \Rightarrow \dfrac{{\pi {r^2}\theta }}{{360^\circ }} = \pi {\left( {20} \right)^2} \times \left( {\dfrac{{360^\circ  - 90^\circ }}{{360^\circ }}} \right)\]

That gives us,

\[ \Rightarrow \dfrac{{\pi {r^2}\theta }}{{360^\circ }} = \dfrac{{22}}{7} \times 400 \times \dfrac{3}{4}\]

Hence,

\[ \Rightarrow \dfrac{{\pi {r^2}\theta }}{{360^\circ }} = 942.85c{m^2}\]

Now, the area of the major segment can be given as,

\[ \Rightarrow \dfrac{{\pi {r^2}\theta }}{{360^\circ }} + \dfrac{1}{2}{r^2} = 942.85 + 200\]

That is,

\[ \Rightarrow \dfrac{{\pi {r^2}\theta }}{{360^\circ }} + \dfrac{1}{2}{r^2} = 1142.85c{m^2}\]

Hence, the area of the major segment is \[1142.85c{m^2}\] .

Sample Question 2 : With the vertices A, B and C of a triangle ABC as centres, arcs are drawn with radii 5 cm each as shown in Fig. 11.15. If AB = 14 cm, BC = 48 cm and CA = 50 cm, then find the area of the shaded region. (Use π = 3.14)

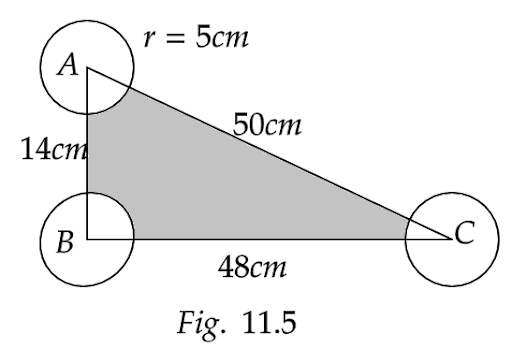
Ans: Given that, a triangle ABC with sides AB = 14 cm, BC = 48 cm and CA = 50 cm

Here, we can observe that,

\[ \Rightarrow {\left( {14} \right)^2} + {\left( {48} \right)^2} = 196 + 2304\]

That is,

\[ \Rightarrow {\left( {14} \right)^2} + {\left( {48} \right)^2} = 2500\]

Hence,

\[ \Rightarrow {\left( {14} \right)^2} + {\left( {48} \right)^2} = {\left( {50} \right)^2}\]

Since the Pythagoras theorem is satisfied, hence the triangle ABC is a right angled triangle.

Now, the area of right triangle ABC is given by,

\[ \Rightarrow \dfrac{1}{2}bh = \dfrac{1}{2} \times 48 \times 14\]

That gives us,

\[ \Rightarrow \dfrac{1}{2}bh = 336c{m^2}\]

Now, the area of three sectors having \[\angle A,\angle B,\angle C\] is given by,

\[ \Rightarrow A = \pi {r^2}\dfrac{{\angle A}}{{360^\circ }} + \pi {r^2}\dfrac{{\angle B}}{{360^\circ }} + \pi {r^2}\dfrac{{\angle C}}{{360^\circ }}\]

Or,

\[ \Rightarrow A = \pi {r^2}\left( {\dfrac{{\angle A}}{{360^\circ }} + \dfrac{{\angle B}}{{360^\circ }} + \dfrac{{\angle C}}{{360^\circ }}} \right)\]

That gives us,

\[ \Rightarrow A = \pi {r^2}\left( {\dfrac{{\angle A + \angle B + \angle C}}{{360^\circ }}} \right)\]

i.e.

\[ \Rightarrow A = \pi {\left( 5 \right)^2}\left( {\dfrac{{180^\circ }}{{360^\circ }}} \right)\]

That is,

\[ \Rightarrow A = 3.14 \times 25 \times \dfrac{1}{2}\]

Hence,

\[ \Rightarrow A = 39.25c{m^2}\]

Now the area of the shaded region is given by,

\[ \Rightarrow \dfrac{1}{2}bh - A = 336 - 39.25\]

Hence,

\[ \Rightarrow \dfrac{1}{2}bh - A = 296.75c{m^2}\]

Therefore, the area of the shaded region is \[296.75c{m^2}\] .

Sample Question 3 : A calf is tied with a rope of length 6 m at the corner of a square grassy lawn of side 20 m. If the length of the rope is increased by 5.5m, find the increase in area of the grassy lawn in which the calf can graze.

Ans: Given that, the width of the square grassy lawn is \[a = 20m\]

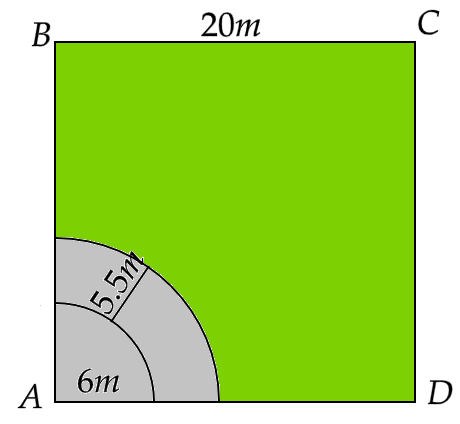
Now the area of the lawn that the calf can graze while being tied to a rope of length \[r = 6m\] is given by,

\[ \Rightarrow \pi {r^2}\dfrac{\theta }{{360^\circ }} = \pi {\left( 6 \right)^2}\left( {\dfrac{{90^\circ }}{{360^\circ }}} \right)\]

That gives us,

\[ \Rightarrow \pi {r^2}\dfrac{\theta }{{360^\circ }} = 3.14 \times 36 \times \dfrac{1}{4}\]

Hence,

\[ \Rightarrow \pi {r^2}\dfrac{\theta }{{360^\circ }} = 28.26{m^2}\]

Now the area of the lawn that the calf can graze while being tied to a rope of length \[R = 6 + 5.5 = 11.5m\] is given by,

\[ \Rightarrow \pi {R^2}\dfrac{\theta }{{360^\circ }} = \pi {\left( {11.5} \right)^2}\left( {\dfrac{{90^\circ }}{{360^\circ }}} \right)\]

That gives us,

\[ \Rightarrow \pi {R^2}\dfrac{\theta }{{360^\circ }} = 3.14 \times 11.5 \times 11.5 \times \dfrac{1}{4}\]

Hence,

\[ \Rightarrow \pi {R^2}\dfrac{\theta }{{360^\circ }} = 103.81{m^2}\]

Now the increase in the area of the grassy lawn in which the calf can graze is given by,

\[ \Rightarrow \pi {R^2}\dfrac{\theta }{{360^\circ }} - \pi {r^2}\dfrac{\theta }{{360^\circ }} = 103.81 - 28.26\]

That gives us,

\[ \Rightarrow \pi {R^2}\dfrac{\theta }{{360^\circ }} - \pi {r^2}\dfrac{\theta }{{360^\circ }} = 75.55{m^2}\]

EXERCISE 11.4

1. The area of a circular playground is \[22176{m^2}\] . Find the cost of fencing this ground at the rate of Rs 50 per m.

Ans: Given that, the area of the circular playground is \[A = 22176{m^2}\]

Now if \[r\] is the radius of the circular playground, then

\[ \Rightarrow \pi {r^2} = 22176{m^2}\]

That is,

\[ \Rightarrow {r^2} = \dfrac{{22176}}{\pi }\]

Or,

\[ \Rightarrow {r^2} = \dfrac{{22176}}{{22}} \times 7\]

Hence,

\[ \Rightarrow {r^2} = 1008 \times 7\]

i.e.

\[ \Rightarrow r = \sqrt {\left( {12 \times 12 \times 7} \right) \times 7} \]

That is,

\[ \Rightarrow r = 12 \times 7 = 84m\]

Now the circumference of the circular playground is,

\[ \Rightarrow 2\pi r = 2 \times \dfrac{{22}}{7} \times 84\]

i.e.

\[ \Rightarrow 2\pi r = 22 \times 24 = 528m\]

Therefore, the cost of fencing this ground at the rate of Rs 50 per metre will be

\[ \Rightarrow 50 \times 2\pi r = 50 \times 528\]

i.e.

\[ \Rightarrow 50 \times 2\pi r = 26400Rs.\]

2. The radius of front and rear wheels of a tractor are 80 cm and 2 m, respectively. Find the number of revolutions that rear wheel will make in covering a distance in which the front wheel makes 1400 revolutions.

Ans: Given that, the radius of front and rear wheels of a tractor are \[{r_1} = 80cm\] and \[{r_2} = 2m = 200cm\]

Let \[{n_1} = 1400\] and \[{n_2}\] be the number of revolutions of the front and rear wheels respectively.

Now since the both wheels cover the same distance,

Hence we have

\[ \Rightarrow 2\pi {r_1}{n_1} = 2\pi {r_2}{n_2}\]

That gives us,

\[ \Rightarrow 2\pi  \cdot 80 \cdot 1400 = 2\pi  \cdot 200 \cdot {n_2}\]

Hence,

\[ \Rightarrow {n_2} = \dfrac{{80 \times 1400}}{{200}}\]

i.e.

\[ \Rightarrow {n_2} = 560\]

3. Sides of a triangular field are 15 m, 16 m and 17 m. With the three corners of the field a cow, a buffalo and a horse are tied separately with ropes of length 7 m each to graze in the field. Find the area of the field which cannot be grazed by three animals.

Ans: Here, the three sides of a triangular field are given as \[a = 15m\] , \[b = 16m\] and \[c = 17m\]

We need to use Heron’s formula to find the area of the triangular field.

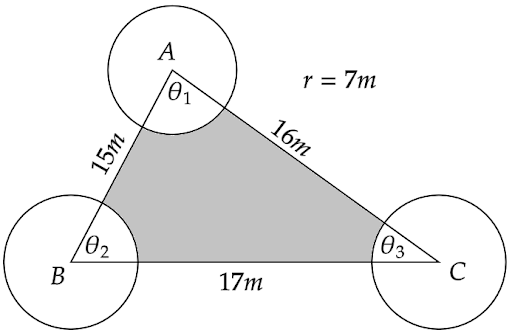
So the semi perimeter of the triangular field is \[s = \dfrac{{a + b + c}}{2}\] i.e. \[s = \dfrac{{15 + 16 + 17}}{2} = \dfrac{{48}}{2}\]

Hence, \[s = 24m\]

Therefore, the area of the triangular field is,

\[A = \sqrt {s\left( {s - a} \right)\left( {s - b} \right)\left( {s - c} \right)} \]

That is,

\[A = \sqrt {24\left( {24 - 15} \right)\left( {24 - 16} \right)\left( {24 - 17} \right)} \]

Or,

\[A = \sqrt {24 \times 9 \times 8 \times 7} \]

i.e.

\[A = 3 \times 4 \times 2 \times \sqrt {3 \times 7} \]

Hence,

\[A = 24\sqrt {21} {m^2}\]

Now the area of the field which is grazed by the cow, buffalo and horse tied to a rope of 7 metres, is equal to the area of three sectors of radius \[r = 7m\] .

Hence, area of the field that is grazed is

\[ \Rightarrow \dfrac{{\pi {r^2}{\theta _1}}}{{360^\circ }} + \dfrac{{\pi {r^2}{\theta _2}}}{{360^\circ }} + \dfrac{{\pi {r^2}{\theta _3}}}{{360^\circ }}\]

That gives us,

\[ \Rightarrow \pi {r^2} \cdot \dfrac{{\left( {{\theta _1} + {\theta _2} + {\theta _3}} \right)}}{{360^\circ }}\]

Since for a triangle, \[\left( {{\theta _1} + {\theta _2} + {\theta _3}} \right) = 180^\circ \]

Therefore,

\[ \Rightarrow \pi {r^2} \cdot \dfrac{{180^\circ }}{{360^\circ }}\]

Putting \[r = 7m\] gives us,

\[ \Rightarrow \pi {\left( 7 \right)^2} \cdot \dfrac{1}{2}\]

Or,

\[ \Rightarrow \dfrac{{49}}{2} \times \dfrac{{22}}{7}\]

Hence,

\[ \Rightarrow 77{m^2}\]

Therefore, the area of the field that is not grazed is,

\[ \Rightarrow \left( {24\sqrt {21}  - 77} \right){m^2}\]

That is approximately an area of \[33{m^2}\] .

4. Find the area of the segment of a circle of radius 12 cm whose corresponding sector central angle 60°. (Use π = 3.14).

Ans: The area of a segment is given by the difference of areas of its corresponding sector and the corresponding triangle.

Here we are given the radius of the circle \[r = 12cm\] and \[\theta  = 60^\circ \]

Hence the area of the sector is,

\[ \Rightarrow \dfrac{{\pi {r^2}\theta }}{{360^\circ }} = \pi {\left( {12} \right)^2} \cdot \dfrac{{60^\circ }}{{360^\circ }}\]

That gives us,

\[ \Rightarrow \dfrac{{\pi {r^2}\theta }}{{360^\circ }} = 144 \times 3.14 \times \dfrac{1}{6}\]

Hence,

\[ \Rightarrow \dfrac{{\pi {r^2}\theta }}{{360^\circ }} = 75.36c{m^2}\]

Now since in the corresponding triangle we have two of its side equal to \[r = 12cm\] and \[\theta  = 60^\circ \]

Hence the other two angles are equal to each other having a measure of \[\dfrac{{180^\circ  - 60^\circ }}{2} = 60^\circ \]

Hence, all the angles of the triangle are \[\theta  = 60^\circ \] so it is an equilateral triangle.

Now, the area of the triangle is given by,

\[ \Rightarrow \dfrac{{\sqrt 3 }}{4}{r^2} = \dfrac{{\sqrt 3 }}{4}{\left( {12} \right)^2}\]

That gives us,

\[ \Rightarrow \dfrac{{\sqrt 3 }}{4}{r^2} = \sqrt 3  \times 12 \times 3\]

Hence,

\[ \Rightarrow \dfrac{{\sqrt 3 }}{4}{r^2} = 36\sqrt 3 \]

Therefore, area of the segment is given by

\[ \Rightarrow \left( {75.36 - 36\sqrt 3 } \right)c{m^2}\]

That is approximately an area of \[13c{m^2}\] .

5. A circular pond is 17.5 m in diameter. It is surrounded by a 2m wide path. Find the cost of constructing the path at the rate of Rs 25 per square metre.

Ans: Given that the diameter of the pond is 17.5 m .

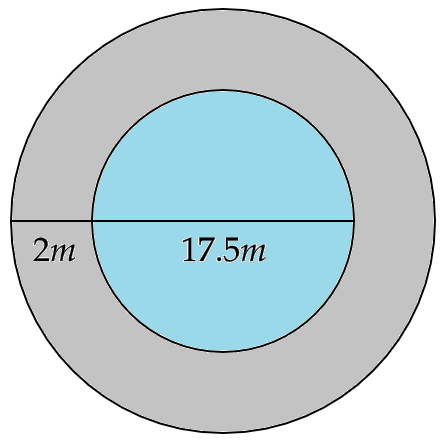
Hence, the radius of the pond is \[{r_1} = \dfrac{{35}}{4}m\]

Since the pond is surrounded by a 2m wide path,

The radius of the path including the pond will be given by \[{r_2} = \dfrac{{35}}{4} + 2 = \dfrac{{43}}{4}m\]

Now, the area of the path will be

\[ \Rightarrow \pi {r_2}^2 - \pi {r_1}^2 = \pi \left( {{r_2}^2 - {r_1}^2} \right) = \pi \left( {{r_2} + {r_1}} \right)\left( {{r_2} - {r_1}} \right)\]

That gives us,

\[ \Rightarrow \pi {r_2}^2 - \pi {r_1}^2 = \pi \left( {\dfrac{{43}}{4} + \dfrac{{35}}{4}} \right)\left( {\dfrac{{43}}{4} - \dfrac{{35}}{4}} \right)\]

Or,

\[ \Rightarrow \pi {r_2}^2 - \pi {r_1}^2 = \pi \left( {\dfrac{{78}}{4}} \right)\left( 2 \right)\]

That is,

\[ \Rightarrow \pi {r_2}^2 - \pi {r_1}^2 = \dfrac{{22}}{7} \cdot 39\]

Hence,

\[ \Rightarrow \pi {r_2}^2 - \pi {r_1}^2 = 122.57{m^2}\]

Therefore, the cost of constructing the path at the rate of Rs 25 per square metre will be

\[ \Rightarrow 25 \times 122.57\]

Hence,

\[ \Rightarrow 3064.25Rs\]

6. In the given figure, ABCD is a trapezium with AB || CD. AB = 18 cm, DC = 32 cm and distance between AB and DC is 14 cm. If arcs of equal radii 7 cm with centres A, B, C and D have been drawn, then find the area of the shaded region of the figure.

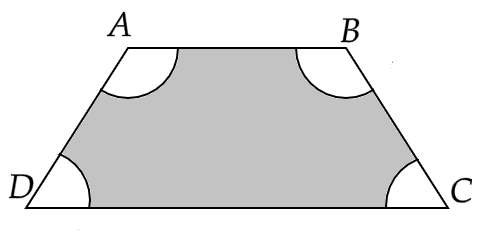
Ans: Given that, the parallel sides of the trapezium ABCD are \[AB = 18cm\] and \[CD = 32cm\]

And the distance between the parallel sides is \[h = 14cm\]

Hence the area of trapezium ABCD is,

\[ \Rightarrow \dfrac{1}{2}\left( {AB + CD} \right)h = \dfrac{1}{2}\left( {18 + 32} \right)14\]

That gives us,

\[ \Rightarrow \dfrac{1}{2}\left( {AB + CD} \right)h = 25 \times 14 = 350c{m^2}\]

Now the area of the unshaded region is equal to the area of four sectors of radius \[r = 7cm\] and also we have \[{\theta _1} + {\theta _2} + {\theta _3} + {\theta _4} = 360^\circ \] for a quadrilateral.

Hence, the area of unshaded region is,

\[ \Rightarrow \dfrac{{\pi {r^2}{\theta _1}}}{{360^\circ }} + \dfrac{{\pi {r^2}{\theta _2}}}{{360^\circ }} + \dfrac{{\pi {r^2}{\theta _3}}}{{360^\circ }} + \dfrac{{\pi {r^2}{\theta _4}}}{{360^\circ }}\]

Or,

\[ \Rightarrow \pi {r^2}\dfrac{{\left( {{\theta _1} + {\theta _2} + {\theta _3} + {\theta _4}} \right)}}{{360^\circ }}\]

That is,

\[ \Rightarrow \pi {\left( 7 \right)^2} \cdot \dfrac{{360^\circ }}{{360^\circ }}\]

Or,

\[ \Rightarrow 49 \times \dfrac{{22}}{7}\]

Hence,

\[ \Rightarrow 154c{m^2}\]

Therefore, the area of the shaded region is,

\[ \Rightarrow 350 - 154\]

Hence,

\[ \Rightarrow 196c{m^2}\]

7. Three circles each of radius 3.5 cm are drawn in such a way that each of them touches the other two. Find the area enclosed between these circles.

Ans: Given that, three circles each of radius \[r = 3.5cm\] are drawn as the figure below.

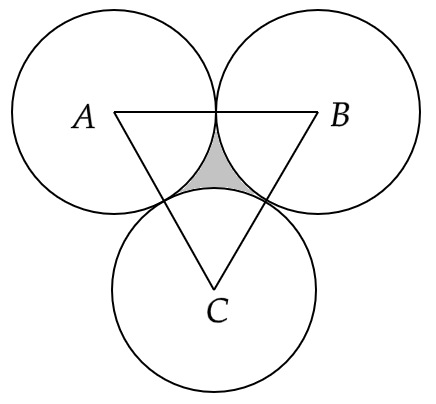
From the figure, we can say that all the three sides of the triangle ABC have a length of \[a = 2r = 7cm\]

Hence, ABC is an equilateral triangle.

Therefore, the area of triangle ABC will be given by,

\[ \Rightarrow \dfrac{{\sqrt 3 }}{4}{a^2} = \dfrac{{\sqrt 3 }}{4}{\left( 7 \right)^2}\]

Hence,

\[ \Rightarrow \dfrac{{\sqrt 3 }}{4}{a^2} = \dfrac{{49\sqrt 3 }}{4}c{m^2}\]

Now the area of three sectors will be given by,

\[ \Rightarrow \dfrac{{\pi {r^2}{\theta _1}}}{{360^\circ }} + \dfrac{{\pi {r^2}{\theta _2}}}{{360^\circ }} + \dfrac{{\pi {r^2}{\theta _3}}}{{360^\circ }}\]

That gives us,

\[ \Rightarrow \pi {r^2}\dfrac{{\left( {{\theta _1} + {\theta _2} + {\theta _3}} \right)}}{{360^\circ }}\]

Or,

\[ \Rightarrow \pi {\left( {\dfrac{7}{2}} \right)^2} \cdot \dfrac{{180^\circ }}{{360^\circ }}\]

That is,

\[ \Rightarrow \dfrac{{22}}{7} \times \dfrac{7}{2} \times \dfrac{7}{2} \times \dfrac{1}{2}\]

Hence,

\[ \Rightarrow \dfrac{{77}}{4}c{m^2}\]

Therefore, area of the shaded region is,

\[ \Rightarrow \dfrac{{49\sqrt 3 }}{4} - \dfrac{{77}}{4}\]

i.e.

\[ \Rightarrow \dfrac{1}{4}\left( {49\sqrt 3  - 77} \right)c{m^2}\]

That is approximately an area of \[1.96c{m^2}\] .

8. Find the area of sector of a circle of radius 5 cm, if the corresponding arc length is 3.5 cm.

Ans: Given that, the radius of the circle is \[r = 5cm\] and an arc length is \[l = 3.5cm\]

Then we have,

\[ \Rightarrow \dfrac{{2\pi r\theta }}{{360^\circ }} = l\]

That gives us,

\[ \Rightarrow \dfrac{{2\pi r\theta }}{{360^\circ }} = 3.5\]

Dividing both sides by 2, we get

\[ \Rightarrow \dfrac{{\pi r\theta }}{{360^\circ }} = \dfrac{7}{4}\]

Multiplying both sides by the radius \[r = 5cm\] , we can write

\[ \Rightarrow \dfrac{{\pi {r^2}\theta }}{{360^\circ }} = \dfrac{7}{4} \times 5\]

Hence, the area of the corresponding sector is,

\[ \Rightarrow \dfrac{{\pi {r^2}\theta }}{{360^\circ }} = \dfrac{{35}}{4} = 8.75c{m^2}\]

9. Four circular cardboard pieces of radii 7 cm are placed on a paper in such a way that each piece touches other two pieces. Find the area of the portion enclosed between these pieces.

Ans: Given that, four circular cardboard pieces each of radius \[r = 7cm\] are placed such as the figure below

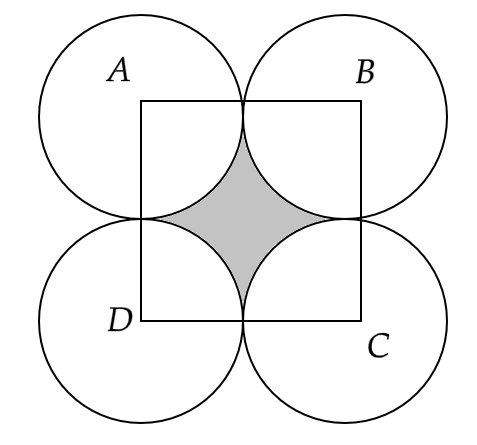
From the figure we can say that the quadrilateral ABCD has each of sides equal to the length of \[a = 2r = 14cm\]

Therefore, ABCD is a square.

Now the area of square ABCD will be given by,

\[ \Rightarrow {a^2} = {\left( {14} \right)^2}\]

That gives us,

\[ \Rightarrow {a^2} = 196c{m^2}\]

Now the area of four sectors with radii \[r = 7cm\] and \[\theta  = 90^\circ \] will be given by,

\[ \Rightarrow 4 \times \pi {r^2} \times \dfrac{\theta }{{360^\circ }}\]

That gives us,

\[ \Rightarrow 4 \times \dfrac{{22}}{7} \times {7^2} \times \dfrac{{90^\circ }}{{360^\circ }}\]

Or,

\[ \Rightarrow 4 \times 22 \times 7 \times \dfrac{1}{4}\]

Hence,

\[ \Rightarrow 154c{m^2}\]

Therefore, area of the portion enclosed between these pieces is,

\[ \Rightarrow 196 - 154\]

Hence,

\[ \Rightarrow 42c{m^2}\]

10. On a square cardboard sheet of area 784 \[c{m^2}\] , four congruent circular plates of maximum size are places such that each circular plate touches the other two plates and each side of square sheet is tangent to two circular plates. Find the area of the square sheet not covered by the circular plates.

Ans: Given that, a square cardboard sheet has area \[{a^2} = 784c{m^2}\]

Hence, its length is \[a = \sqrt {784}  = 28cm\]

Now, four congruent circular plates of maximum size are placed which touch two of the other plates.

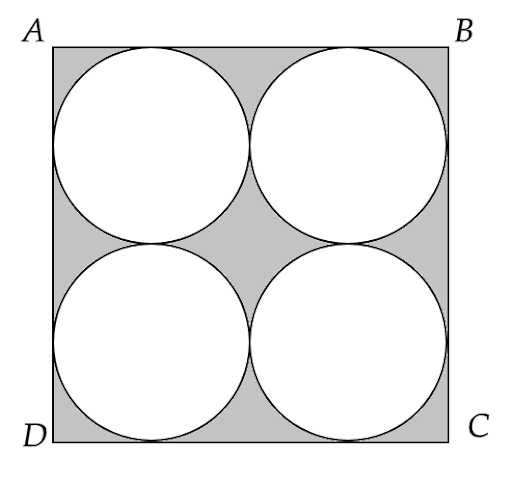
From the figure, we can say that the diameter of each circle is equal to half of the length of the square, i.e. \[d = \dfrac{a}{2} = 14cm\]

Hence, \[r = \dfrac{d}{2} = 7cm\]

Now the area of four circles of radii \[r = 7cm\] is given by

\[ \Rightarrow 4\pi {r^2} = 4 \times \dfrac{{22}}{7} \times {\left( 7 \right)^2}\]

That gives us,

\[ \Rightarrow 4\pi {r^2} = 4 \times 22 \times 7\]

i.e.

\[ \Rightarrow 4\pi {r^2} = 616c{m^2}\]

Therefore, the area of the square sheet that is not covered by the circular plates is,

\[ \Rightarrow 784 - 616\]

Hence,

\[ \Rightarrow 168c{m^2}\]

11. Floor of a room is of dimensions 5m × 4 m and it is covered with circular tiles of diameters 50 cm each as shown in figure. Find the area of the floor that remains uncovered with tiles. (Use π = 3.14)

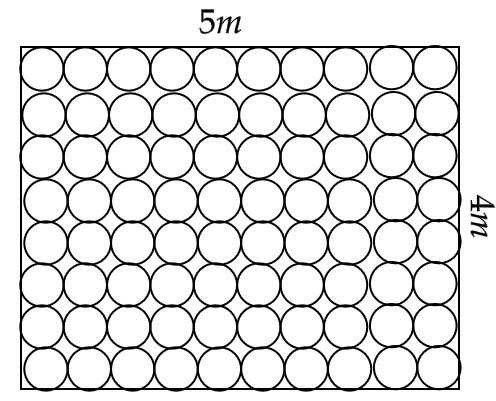
Ans: Given that, the dimensions of the floor are \[l = 5m\] and \[b = 4m\]

Hence, area of the floor is

\[ \Rightarrow l \times b = 5 \times 4 = 20{m^2}\]

Now, from the figure we can say that the number of tiles is \[10 \times 8 = 80\]

The diameter of each tile is given as \[d = 0.5m\] hence its radius is \[r = 0.25m\]

Now the area covered by 80 circular tiles of radius \[r = 0.25m\] is given by,

\[ \Rightarrow 80 \times \pi {r^2} = 80 \times 3.14 \times {\left( {0.25} \right)^2}\]

That is,

\[ \Rightarrow 80 \times \pi {r^2} = 80 \times 3.14 \times \dfrac{1}{4} \times \dfrac{1}{4}\]

Hence,

\[ \Rightarrow 80 \times \pi {r^2} = 15.7{m^2}\]

Therefore, the area of the floor that remains uncovered with tiles is,

\[ \Rightarrow 20 - 15.7\]

i.e.

\[ \Rightarrow 4.3{m^2}\]

12. All the vertices of a rhombus lie on a circle. Find the area of the rhombus if area of the circle is 1256 cm2. (Use π = 3.14)

Ans: Given that, all the vertices of a rhombus lie on a circle i.e. a rhombus is inscribed in a circle.

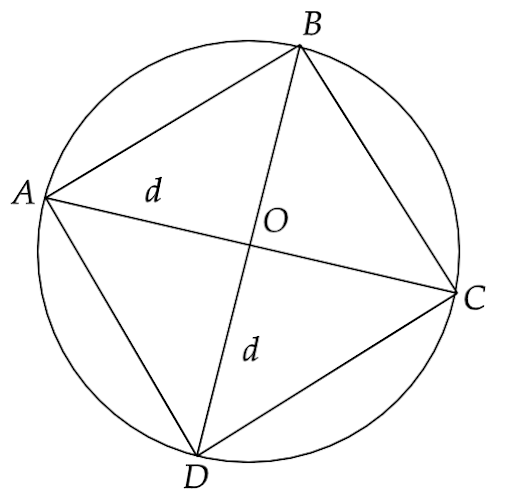
Also, area of the circle is given as,

\[ \Rightarrow \pi {r^2} = 1256c{m^2}\]

That gives us,

\[ \Rightarrow {r^2} = \dfrac{{1256}}{{3.14}}\]

Or,

\[ \Rightarrow {r^2} = \dfrac{{1256}}{{314}} \times 100\]

That is,

\[ \Rightarrow {r^2} = 4 \times 100\]

i.e.

\[ \Rightarrow r = 2 \times 10\]

Hence,

\[ \Rightarrow r = 20cm\]

Now since the vertices of the rhombus lie on the circle, hence the diagonals of the rhombus are equal to the diameter of the circle, i.e. \[{d_1} = {d_2} = 2r = 40cm\]

Therefore, area of the rhombus is given by,

\[ \Rightarrow \dfrac{1}{2}{d_1}{d_2} = \dfrac{1}{2} \times 40 \times 40\]

Hence,

\[ \Rightarrow \dfrac{1}{2}{d_1}{d_2} = 800c{m^2}\]

13. An archery target has three regions formed by three concentric circles as shown in figure. If the diameters of the concentric circles are in the ratio 1 : 2 : 3, then find the ratio of the areas of three regions.

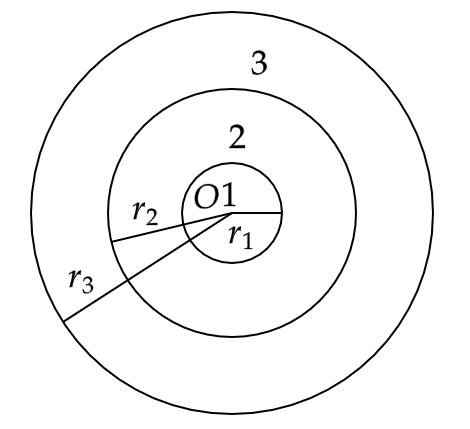
Ans: Given that, the ratio of diameters of three concentric circles is \[1:2:3\]

Hence, the ratio of their radii will also be \[1:2:3\]

Let their radii be \[r\] , \[2r\] and \[3r\] respectively.

Then area of region 1 is,

\[ \Rightarrow \pi {r^2}\]

Area of region 2 is,

\[ \Rightarrow \pi {\left( {2r} \right)^2} - \pi {r^2} = 4\pi {r^2} - \pi {r^2}\]

i.e.

\[ \Rightarrow \pi {\left( {2r} \right)^2} - \pi {r^2} = 3\pi {r^2}\]

Area of region 3 is,

\[ \Rightarrow \pi {\left( {3r} \right)^2} - \pi {\left( {2r} \right)^2} = 9\pi {r^2} - 4\pi {r^2}\]

i.e.

\[ \Rightarrow \pi {\left( {3r} \right)^2} - \pi {\left( {2r} \right)^2} = 5\pi {r^2}\]

Therefore, the ratio of areas of three regions is,

\[ \Rightarrow \pi {r^2}:3\pi {r^2}:5\pi {r^2}\]

i.e.

\[ \Rightarrow 1:3:5\]

14. The length of minute hand of a clock is 5 cm. Find the area swept by the minute hand during the time 6 : 05 am and 6 : 40 am.

Ans: The time duration between 6 : 05 am and 6 : 40 am is 35 minutes.

In 35 minutes, the minute hand makes an angle \[\theta  = \dfrac{{35}}{{60}} \times 360^\circ  = 210^\circ \]

Now, consider \[r = 5cm\]

Then the area swept by the minute hand during the time 6 : 05 am and 6 : 40 am will be given by,

\[ \Rightarrow \pi {r^2} \cdot \dfrac{\theta }{{360^\circ }}\]

That gives us,

\[ \Rightarrow \pi {\left( 5 \right)^2} \cdot \dfrac{{210^\circ }}{{360^\circ }}\]

Or,

\[ \Rightarrow 25 \times \dfrac{{22}}{7} \times \dfrac{7}{{12}}\]

Hence,

\[ \Rightarrow 45.83c{m^2}\]

15. Area of sector of central angle 200° of a circle is 770 \[c{m^2}\]. Find the length of the corresponding arc of this sector.

Ans: Given that, the area of sector of a circle is \[A = 770c{m^2}\] where \[\theta  = 200^\circ \]

That gives us,

\[ \Rightarrow \pi {r^2} \cdot \dfrac{\theta }{{360^\circ }} = A\]

Or,

\[ \Rightarrow {r^2} = \dfrac{A}{\pi } \times \dfrac{{360^\circ }}{\theta }\]

Hence,

\[ \Rightarrow {r^2} = \dfrac{{770}}{{22}} \times 7 \times \dfrac{{360^\circ }}{{200^\circ }}\]

Or,

\[ \Rightarrow {r^2} = \dfrac{{70}}{2} \times 7 \times \dfrac{9}{5}\]

i.e.

\[ \Rightarrow {r^2} = 7 \times 7 \times 3 \times 3\]

Hence,

\[ \Rightarrow r = 7 \times 3 = 21cm\]

Now, the corresponding arc length will be given by,

\[ \Rightarrow l = 2\pi r \cdot \dfrac{\theta }{{360^\circ }}\]

That gives us,

\[ \Rightarrow l = 2 \times \dfrac{{22}}{7} \times 21 \times \dfrac{{200^\circ }}{{360^\circ }}\]

Hence,

\[ \Rightarrow l = \dfrac{{220}}{3}\]

i.e.

\[ \Rightarrow l = 73.33cm\]

16. The central angles of two sectors of circles of radii 7 cm and 21 cm are respectively 120° and 40°. Find the areas of the two sectors as well as the lengths of the corresponding arcs. What do you observe?

Ans: Given that, two circles of radii \[{r_1} = 7cm\] and \[{r_2} = 21cm\] with the central angles \[{\theta _1} = 120^\circ \] and \[{\theta _2} = 40^\circ \] respectively.

Now their areas of sectors are,

\[ \Rightarrow {A_1} = \pi {r_1}^2 \cdot \dfrac{{{\theta _1}}}{{360^\circ }}\]

That is,

\[ \Rightarrow {A_1} = \pi {\left( 7 \right)^2} \cdot \dfrac{{120^\circ }}{{360^\circ }}\]

Or,

\[ \Rightarrow {A_1} = 22 \times 7 \times \dfrac{1}{3}\]

Hence,

\[ \Rightarrow {A_1} = \dfrac{{154}}{3}c{m^2}\]

And,

\[ \Rightarrow {A_2} = \pi {r_2}^2 \cdot \dfrac{{{\theta _2}}}{{360^\circ }}\]

That gives us,

\[ \Rightarrow {A_2} = \pi {\left( {21} \right)^2} \cdot \dfrac{{40^\circ }}{{360^\circ }}\]

Or,

\[ \Rightarrow {A_2} = 22 \times 3 \times 21 \times \dfrac{1}{9}\]

Hence,

\[ \Rightarrow {A_2} = 154c{m^2}\]

Therefore, the area of sector of the second circle is three times than that of the first circle.

Now, their arc lengths will be given by

\[ \Rightarrow {l_1} = 2\pi {r_1} \cdot \dfrac{{{\theta _1}}}{{360^\circ }}\]

That gives us,

\[ \Rightarrow {l_1} = 2 \times \dfrac{{22}}{7} \times 7 \times \dfrac{{120^\circ }}{{360^\circ }}\]

That is,

\[ \Rightarrow {l_1} = 2 \times 22 \times \dfrac{1}{3}\]

Hence,

\[ \Rightarrow {l_1} = \dfrac{{44}}{3}cm\]

And,

\[ \Rightarrow {l_2} = 2\pi {r_2} \cdot \dfrac{{{\theta _2}}}{{360^\circ }}\]

That gives us,

\[ \Rightarrow {l_2} = 2 \times \dfrac{{22}}{7} \times 21 \times \dfrac{{40^\circ }}{{360^\circ }}\]

That is,

\[ \Rightarrow {l_2} = 2 \times 22 \times 3 \times \dfrac{1}{9}\]

Hence,

\[ \Rightarrow {l_2} = \dfrac{{44}}{3}\]

Therefore, both circles have the same arc length.

17. Find the area of the shaded region given in figure here.

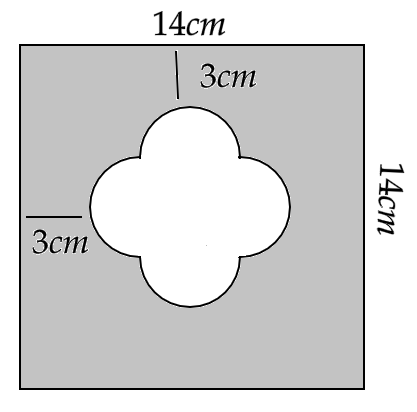
Ans: First we have to find the area of the unshaded region which is made up of 4 semicircles and a square.

Now the diameter of each semicircle can be given by,

\[ \Rightarrow 14 - 3 - 3 = 2d\]

That gives us,

\[ \Rightarrow d = 4cm\]

Hence, the radius of each semicircle is \[r = 2cm\]

Now the area of four semicircles of radius \[r = 2cm\] is given by,

\[ \Rightarrow 4 \times \dfrac{1}{2} \times \pi {r^2} = 2\pi {\left( 2 \right)^2}\]

Hence,

\[ \Rightarrow 4 \times \dfrac{1}{2} \times \pi {r^2} = 8\pi c{m^2}\]

Now the length of the unshaded square is equal to the diameter of the semicircle, i.e. \[a = d = 4cm\]

Hence, area of the unshaded square is,

\[ \Rightarrow {a^2} = {4^2} = 16c{m^2}\]

Total area of the unshaded region is,

\[ \Rightarrow \left( {8 \times 3.14} \right) + 16\]

Hence,

\[ \Rightarrow 41.12c{m^2}\]

Now, area of the whole square is,

\[ \Rightarrow 14 \times 14 = 196c{m^2}\]

Hence, area of the shaded region is,

\[ \Rightarrow 196 - 41.12\]

i.e.

\[ \Rightarrow 154.88c{m^2}\]

18. Find the number of revolutions made by circular wheel of area 1.54 \[{m^2}\] in rolling a distance of 176 m.

Ans: Given that, the area of a circular wheel is \[A = 1.54{m^2}\]

Therefore,

\[ \Rightarrow \pi {r^2} = A\]

Or,

\[ \Rightarrow \dfrac{{22}}{7} \cdot {r^2} = 1.54\]

That is,

\[ \Rightarrow {r^2} = \dfrac{{154}}{{100}} \times \dfrac{7}{{22}}\]

That gives us,

\[ \Rightarrow {r^2} = \dfrac{7}{{100}} \times 7\]

Hence,

\[ \Rightarrow r = \dfrac{7}{{10}}\]

Now, if the wheel take n revolutions to cover a distance of 176m then we can write,

\[ \Rightarrow 2\pi rn = 176\]

That gives,

\[ \Rightarrow n = \dfrac{{176}}{{2\pi r}}\]

That is,

\[ \Rightarrow n = \dfrac{{176 \times 7 \times 10}}{{2 \times 22 \times 7}}\]

Hence,

\[ \Rightarrow n = 40\]

19. Find the difference of the areas of two segments of a circle formed by a chord of length 5 cm subtending angle of 90° at the centre.

Ans: Let a chord of a circle be \[AB = 5cm\] which subtends a right angle at the centre O.

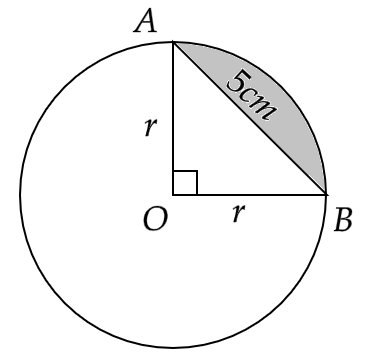
Now is the radius of the circle is \[r\] , then in triangle AOB,we have

\[ \Rightarrow {r^2} + {r^2} = {\left( 5 \right)^2}\]

i.e.

\[ \Rightarrow r = \dfrac{5}{{\sqrt 2 }}cm\]

Now the area of triangle AOB is given by,

\[ \Rightarrow \dfrac{1}{2}{r^2} = \dfrac{{25}}{4}c{m^2}\]

Now area of the minor segment is,

\[ \Rightarrow \dfrac{{\pi {r^2}}}{4} - \dfrac{{25}}{4}\]

That is,

\[ \Rightarrow \dfrac{{25\pi  - 50}}{8}c{m^2}\]

And area of the major segment is,

\[ \Rightarrow \dfrac{{3\pi {r^2}}}{4} + \dfrac{{25}}{4}\]

That is,

\[ \Rightarrow \dfrac{{75\pi  + 50}}{8}c{m^2}\]

Hence, the difference between the areas of major and minor segments is,

\[ \Rightarrow \dfrac{{75\pi  + 50}}{8} - \dfrac{{25\pi  - 50}}{8}\]

That gives us,

\[ \Rightarrow \dfrac{{75\pi  + 50 - 25\pi  + 50}}{8}\]

i.e.

\[ \Rightarrow \dfrac{{50\pi  + 100}}{8}\]

Hence,

\[ \Rightarrow \dfrac{{25}}{4}\left( {\pi  + 2} \right)c{m^2}\]

20. Find the difference of the areas of a sector of angle 120° and its corresponding major sector of a circle of radius 21 cm.

Ans: Given that, a circle of radius \[r = 21cm\] and a central angle of sector \[{\theta _1} = 120^\circ \]

Now, if \[{\theta _1} = 120^\circ \] is the central angle of minor sector, then for the major sector the central angle will be \[{\theta _2} = 360^\circ  - 120^\circ  = 240^\circ \]

Now the difference between the areas of major and minor sector is given by,

\[ \Rightarrow \pi {r^2} \cdot \dfrac{{{\theta _2}}}{{360^\circ }} - \pi {r^2} \cdot \dfrac{{{\theta _1}}}{{360^\circ }}\]

That gives us,

\[ \Rightarrow \pi {r^2} \cdot \dfrac{{\left( {{\theta _2} - {\theta _1}} \right)}}{{360^\circ }}\]

i.e.

\[ \Rightarrow \dfrac{{22}}{7} \times 21 \times 21 \times \dfrac{{\left( {240^\circ  - 120^\circ } \right)}}{{360^\circ }}\]

Hence,

\[ \Rightarrow 22 \times 21 \times 3 \times \dfrac{{120^\circ }}{{360^\circ }}\]

Or,

\[ \Rightarrow 22 \times 21 \times 3 \times \dfrac{1}{3}\]

Therefore,

\[ \Rightarrow 462c{m^2}\]

What is NCERT Exemplar Class 10 Maths Chapter 11 all About?

NCERT exemplar for Class 10 Maths Chapter 11 - areas related to circles are available in PDF format for free at Vedantu.com. The PDF is prepared as per CBSE book guidelines. The NCERT exemplar for chapter areas related to circles is designed by the expert faculty of Vedantu according to the latest CBSE syllabus. By using this exemplar, students can enhance their preparations while practicing the questions one after. 

These exemplars are explained step by step for the students so that they can understand each and every concept that is important for their exams. Students can easily clear their doubts by solving the detailed solutions to all the questions possible in the chapter areas related to circles and can study effectively for the exams. 

These exemplars help students to get solved questions that give them a clear idea of the formulas and how to use them to find the answers. The listed below topics are covered by the NCERT exemplar for Class 10 chapter 11 - areas related to circles-

• To find the area and perimeter of circles

• To find the segment and areas of the sector of a circle

• To find the areas of a combination of plane figures.

Chapter 11 areas related to circles of Class 10 given in the textbooks have been especially learning the concept of perimeter and area of a circle. Through the exemplar, students will get their theoretical concepts for a better understanding of the concepts they have learned by solving the problems related to areas of the circle. 

Benefits of  Using Vedantu Solutions for NCERT Exemplar Class 10 Chapter 11

Chapter 11 area related to circles has tricky questions. Vedantu provides a Free NCERT exemplar PDF for the respective chapter. Students can learn and practice through this exemplar and can clear their doubts during the live sessions conducted by the expert faculty of Vedantu. Vedantu also provides notes, and question papers for the respective chapter for the students so that they can easily score good marks in their examinations. The students who follow the exemplar to the fullest will remain a step ahead of their mates and will experience a totally new format of learning through online learning.

Till the time schools will open, students have this opportunity to learn by being at their homes. All the online classes can be replayed for any reference to their doubts. Also, the faculty gives live sessions where students can ask their doubts. They can directly communicate with their teachers which gives them a plus point. 

Why wait then? Get the perfect solution for Class 10 chapter 11 NCERT Exemplar today from Vedantu and make your study material for mathematics complete. Use these solutions formulated by the experts to understand the concepts behind solving critical problems given in the exercise. Learn how to manage your time whole solving these problems and build a strategy to score more in the board exams.

Significance of NCERT Exemplar Class 10 Maths Areas Related to Circles Solutions

Determining the area of a circle or its part is what you will learn in this chapter. You will be introduced to new concepts and principles related to the geometric elements of a circle and formulas to determine their values.

Learning these concepts, formulas and their derivations will need a practice ground. For this, students often choose to solve the NCERT Exemplar and fortify their foundation. They also prefer using the solutions for these exercises to find accurate measures to attempt to answer such questions.

Hence, the NCERT Exemplar solutions for Class 10 Areas Related to Circles will become a significant part of your study material.

Advantages of using CBSE Class 10 Areas Related to Circles Exemplar Solutions

• Get a consolidated platform to find the answers to NCERT Exemplar questions. Learn how to proceed with a circle problem and solve it precisely.

• Resolve doubts on your own when you have exemplary solutions in your hands. There is no need to wait to clarify your doubts. Proceed with your preparation and complete preparing this chapter by using this solution.

• Follow the precise answering formats composed by the experts. Check how the experts have skillfully answered certain questions and practice accordingly. Develop your answering skills to score more in the exams.