Maths Notes for Chapter 3 How Many Squares Class 5 - FREE PDF Download
FAQs on How Many Squares Class 5 Maths Chapter 3 CBSE Notes - 2025-26
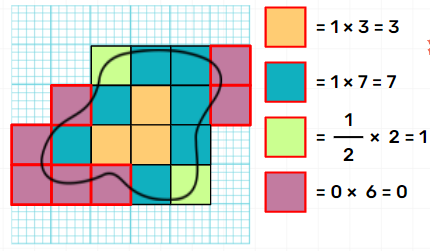
1. Can I measure areas of irregular shapes?
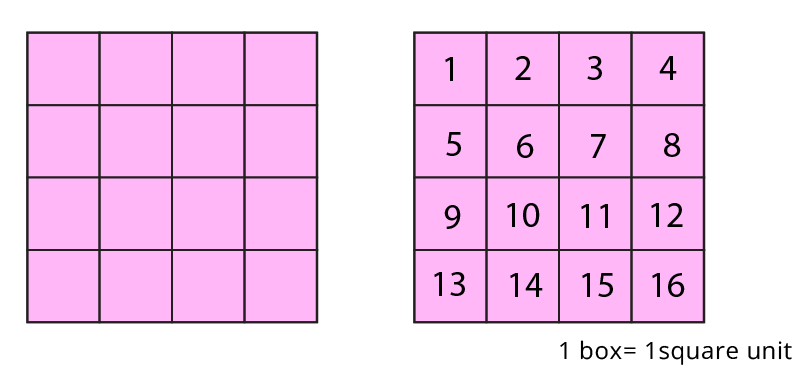
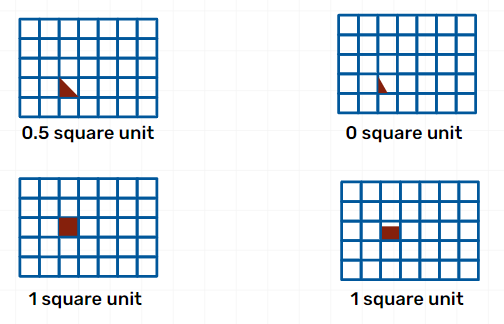
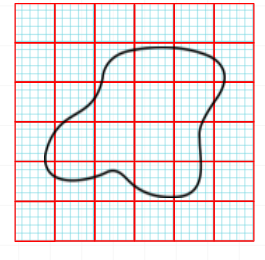
NCERT Maths Class 5 Chapter 3 explains how the irregular shapes are plotted on paper with smaller equal squares drawn on them. Start counting the squares and add them to get the rough area of an irregular shape.
2. How to learn concepts related to areas of rectangles and triangles?
It is easier to learn how to determine the area of triangles and rectangles using smaller square units. You will also be able to correlate these fundamental concepts with advanced geometrical theorems later.
3. Can I download the NCERT Solutions for Class 5 Maths Chapter 3 How Many Squares for free?
Yes you can download the NCERT Solutions for Maths Class 5 Chapter 3 for free from Vedantu. Refer to these NCERT Solutions to determine how our experts have solved the exercise problems effectively.
4. What topics are covered in the "How Many Squares" chapter?
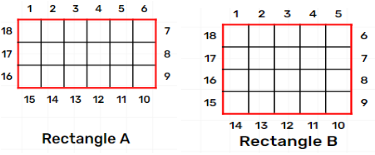
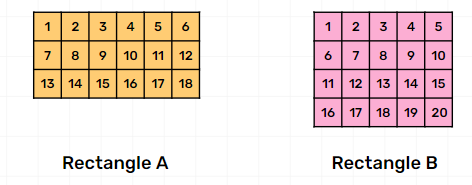
The chapter covers various topics, including identifying different orientations of squares, counting squares in a grid, finding squares in a given pattern, and exploring patterns in real-life scenarios.
5. Is the free PDF download of Class 5 Notes a comprehensive resource?
Yes, the free PDF download provides valuable notes, explanations, examples, and exercises that help students grasp the concepts effectively and reinforce their learning.