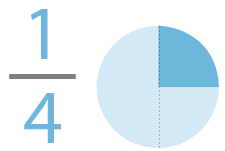Class 4 Maths Chapter 9 Summary Notes PDF Download
FAQs on Halves and Quarters Class 4 Maths Chapter 9 CBSE Notes - 2025-26
1. Is a half bigger than a quarter?
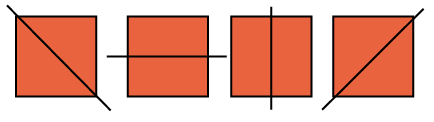
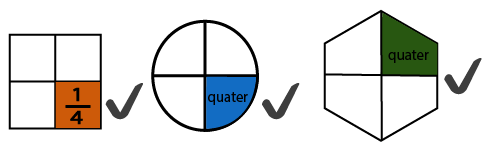
A half is represented by ½ and a quarter is represented by ¼. We have studied that if the denominator is bigger in one fraction than the other one, then the former one is smaller. Here denominator 4 is bigger than denominator 2. Hence, a half is bigger than a quarter.
2. How can I experiment to find out whether a half is bigger than a quarter?
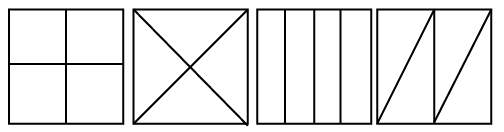
If you tear a page into two halves and then tear half of the page into two halves, you will get a quarter of that full page.
3. How can I study this chapter?
Study the concepts and solve the exercise questions first. Practice using the worksheets and revise the notes before an exam.
Recently Updated Pages
Conic Sections Class 10 Notes CBSE Maths Chapter 11 [PDF]

Khelen Mein Ko Kaako Gusaaiyaan, Murli Tau Gupalhin Bhaavati Class 11 Hindi Antra Notes - Free PDF

Arey In Dohun Raah na Paayi, Balam Aavo Hamare Geh re Class 11 Hindi Antra Notes - Free PDF

Glory at Twilight Class 11 English Woven Words Notes - Free PDF

Cbse Class 11 English Woven Words Notes Chapter 4 Essay

Hasi ki Chot, Sapna, Darbar Class 11 Hindi Antra Notes - Free PDF

Trending pages
CBSE Class 3 to 12 All Subjects Revision CBSE Notes - 2025-26

Hudhud Class 4 Hindi Chapter 13 CBSE Notes - 2025-26

Electric Charges and Fields Class 12 Physics Chapter 1 CBSE Notes - 2025-26

Class 12 Physics CBSE Notes - 2025-26

Class 10 Science All Chapters CBSE Notes - 2025-26

Class 10 Social Science CBSE Notes - 2025-26

Other Pages
Number to Words Converter – Translate Numbers to Words Easily

What is Savitribai Phule Jayanti and Why Is It Celebrated in 2026?

Full Stop in English Grammar: Definition, Rules & Usage

Leap Year: Meaning, Rules & Examples

What is the Full Form of AM and PM?

Essay on New Year 2026: Meaning, Celebrations, and Reflection