NCERT Exemplar for Class 11 Maths Chapter 3 - Trigonometric Functions (Book Solutions)

Examples

Short Answer Type

Example 1: A circular wire of radius \[3cm\] is cut and bent so as to lie along the circumference of a hoop whose radius is  $48cm$ . Find the angle in degrees which is subtended at the centre of hoop.

Ans: Given that, radius of circular wire = $3cm$ 

When it is cut then its length becomes $2\pi  \times 3$ = $6\pi $ 

Again, it is being placed along a circular hoop of radius $48cm$. 

The length $\left( s \right)$ of the arc = $6\pi $

Radius of circle, $r = 48cm$ 

Therefore, the angle $\theta $ (in radian) subtended by the arc at the centre of circle is given by

$ \Rightarrow \theta  = \dfrac{{Arc}}{{Radius}}$ 

$ \Rightarrow \theta  = \dfrac{{6\pi }}{{48}}$

$ \Rightarrow \theta  = \dfrac{\pi }{8}$

$ \Rightarrow \theta  = 22.5^\circ $

Example 2: If $A = {\cos ^2}\theta  + {\sin ^4}\theta $ for all values of $\theta $, then prove that $\dfrac{3}{4} \leqslant A \leqslant 1$

Ans: Given that, $A = {\cos ^2}\theta  + {\sin ^4}\theta $ 

$ \Rightarrow A = {\cos ^2}\theta  + {\sin ^2}\theta {\sin ^2}\theta  \leqslant {\cos ^2}\theta  + {\sin ^2}\theta $

We know that ${\sin ^2}\theta  + {\cos ^2}\theta  = 1$. Hence, we get

$ \Rightarrow A = {\cos ^2}\theta  + {\sin ^2}\theta {\sin ^2}\theta  \leqslant 1.......\left( i \right)$

Now, $A = {\cos ^2}\theta  + {\sin ^4}\theta $

We know that ${\sin ^2}\theta  + {\cos ^2}\theta  = 1$. So, we can write above written equation as,

$ \Rightarrow A = \left( {1 - {{\sin }^2}\theta } \right) + {\sin ^4}\theta $

$ \Rightarrow A = {\sin ^4}\theta  - {\sin ^2}\theta  + 1$

Add $\dfrac{1}{4}$ from RHS and subtract $\dfrac{1}{4}$ from the RHS

$ \Rightarrow A = {\sin ^4}\theta  - {\sin ^2}\theta  + \dfrac{1}{4} + 1 - \dfrac{1}{4}$

$ \Rightarrow A = {\left( {{{\sin }^2}\theta  - \dfrac{1}{2}} \right)^2} + \dfrac{{4 - 1}}{4}$

$ \Rightarrow A = {\left( {{{\sin }^2}\theta  - \dfrac{1}{2}} \right)^2} + \dfrac{3}{4}$

Therefore, $A = {\left( {{{\sin }^2}\theta  - \dfrac{1}{2}} \right)^2} + \dfrac{3}{4} \geqslant \dfrac{3}{4}......\left( {ii} \right)$

Thus, from equation $\left( i \right)$ and $\left( {ii} \right)$, we get

$ \Rightarrow \dfrac{3}{4} \leqslant A \leqslant 1$

Example 3: Find the value of $\sqrt 3 \cos ec20^\circ  - \sec 20^\circ $ 

Ans: We have, $\sqrt 3 \cos ec20^\circ  - \sec 20^\circ $

We can also write it as,

$ \Rightarrow \dfrac{{\sqrt 3 }}{{\sin 20^\circ }} - \dfrac{1}{{\cos 20^\circ }}$

$ \Rightarrow \dfrac{{\sqrt 3 \cos 20^\circ  - \sin 20^\circ }}{{\sin 20^\circ \cos 20^\circ }}$

Multiply and divide numerator by $2$ 

$ \Rightarrow \dfrac{{2\left( {\dfrac{{\sqrt 3 }}{2}\cos 20^\circ  - \dfrac{1}{2}\sin 20^\circ } \right)}}{{\sin 20^\circ \cos 20^\circ }}$

We know that $\dfrac{{\sqrt 3 }}{2} = \sin 60^\circ $ and $\dfrac{1}{2} = \cos 60^\circ $. So, we can write above-written expression as,

$ \Rightarrow \dfrac{{2\left( {\sin 60^\circ \cos 20^\circ  - \cos 60^\circ \sin 20^\circ } \right)}}{{\sin 20^\circ \cos 20^\circ }}$

We know that $\sin \left( {A - B} \right) = \sin A\cos B - \cos A\sin B$. Therefore, we get

$ \Rightarrow \dfrac{{2\sin \left( {60^\circ  - 20^\circ } \right)}}{{\sin 20^\circ \cos 20^\circ }}$

Multiply and divide the above-written expression by $2$ 

$ \Rightarrow \dfrac{{2 \times 2\sin \left( {60^\circ  - 20^\circ } \right)}}{{2\sin 20^\circ \cos 20^\circ }}$

We know that $2\sin x\cos x = \sin 2x$. Therefore, we get

$ \Rightarrow \dfrac{{4\sin \left( {60^\circ  - 20^\circ } \right)}}{{\sin 2 \times 20^\circ }}$

$ \Rightarrow \dfrac{{4\sin 40^\circ }}{{\sin 40^\circ }}$

$ \Rightarrow 4$

Example 4: If $\theta $ lies in the second quadrant, then show that $\sqrt {\dfrac{{1 - \sin \theta }}{{1 + \sin \theta }}}  + \sqrt {\dfrac{{1 + \sin \theta }}{{1 - \sin \theta }}}  =  - 2\sec \theta $ 

Ans: We have, $\sqrt {\dfrac{{1 - \sin \theta }}{{1 + \sin \theta }}}  + \sqrt {\dfrac{{1 + \sin \theta }}{{1 - \sin \theta }}}  =  - 2\sec \theta $

Take LHS,

$ \Rightarrow \sqrt {\dfrac{{1 - \sin \theta }}{{1 + \sin \theta }}}  + \sqrt {\dfrac{{1 + \sin \theta }}{{1 - \sin \theta }}} $

$ \Rightarrow \sqrt {\dfrac{{\left( {1 - \sin \theta } \right)\left( {1 - \sin \theta } \right)}}{{\left( {1 + \sin \theta } \right)\left( {1 - \sin \theta } \right)}}}  + \sqrt {\dfrac{{\left( {1 + \sin \theta } \right)\left( {1 + \sin \theta } \right)}}{{\left( {1 + \sin \theta } \right)\left( {1 + \sin \theta } \right)}}} $

$ \Rightarrow \sqrt {\dfrac{{{{\left( {1 - \sin \theta } \right)}^2}}}{{\left( {{1^2} - {{\sin }^2}\theta } \right)}}}  + \sqrt {\dfrac{{{{\left( {1 + \sin \theta } \right)}^2}}}{{\left( {{1^2} - {{\sin }^2}\theta } \right)}}} $

$ \Rightarrow \dfrac{{\left( {1 - \sin \theta } \right)}}{{\sqrt {\left( {{1^2} - {{\sin }^2}\theta } \right)} }} + \dfrac{{\left( {1 + \sin \theta } \right)}}{{\sqrt {\left( {{1^2} - {{\sin }^2}\theta } \right)} }}$

$ \Rightarrow \dfrac{{1 - \sin \theta  + 1 + \sin \theta }}{{\sqrt {\left( {{1^2} - {{\sin }^2}\theta } \right)} }}$

$ \Rightarrow \dfrac{2}{{\sqrt {\left( {{1^2} - {{\sin }^2}\theta } \right)} }}$

We know that ${\sin ^2}\theta  + {\cos ^2}\theta  = 1$. Therefore, we get

$ \Rightarrow \dfrac{2}{{\sqrt {\cos \theta } }}$

$ \Rightarrow \dfrac{2}{{\left| {\cos \theta } \right|}}$

(Since $\sqrt {{\alpha ^2}}  = \left| \alpha  \right|$ for every real number $\alpha $ )

Given that, $\theta $ lies in second quadrant and we know that in second quadrant $\cos $ is negative. Therefore, we get

$ \Rightarrow \dfrac{2}{{ - \cos \theta }}$

$ \Rightarrow  - 2\sec \theta $

Hence proved

Example 5: Find the value of $\tan 9^\circ  - \tan 27^\circ  - \tan 63^\circ  + \tan 81^\circ $ 

Ans: We have, $\tan 9^\circ  - \tan 27^\circ  - \tan 63^\circ  + \tan 81^\circ $

$ \Rightarrow \tan 9^\circ  + \tan 81^\circ  - \tan 27^\circ  - \tan 63^\circ $

$ \Rightarrow \tan 9^\circ  + \tan \left( {90^\circ  - 9^\circ } \right) - \tan 27^\circ  - \tan \left( {90^\circ  - 27^\circ } \right)$

We know that $\tan \left( {90^\circ  - \theta } \right) = \cos \theta $. Therefore, we get

$ \Rightarrow \tan 9^\circ  + \cot 9^\circ  - \tan 27^\circ  - \cot 27^\circ $

$ \Rightarrow \tan 9^\circ  + \cot 9^\circ  - \left( {\tan 27^\circ  + \cot 27^\circ } \right)$

Now, we will write the above-written expression in terms of $\sin e$ and $\cos ine$.

$ \Rightarrow \dfrac{{\sin 9^\circ }}{{\cos 9^\circ }} + \dfrac{{\cos 9^\circ }}{{\sin 9^\circ }} - \left( {\dfrac{{\sin 27^\circ }}{{\cos 27^\circ }} + \dfrac{{\cos 27^\circ }}{{\sin 27^\circ }}} \right)$

Take LCM

$ \Rightarrow \dfrac{{\sin 9^\circ  \times \sin 9^\circ  + \cos 9^\circ  \times \cos 9^\circ }}{{\sin 9^\circ \cos 9^\circ }} - \left( {\dfrac{{\sin 27^\circ  \times \sin 27^\circ  + \cos 27^\circ  \times \cos 27^\circ }}{{\sin 27^\circ \cos 27^\circ }}} \right)$

$ \Rightarrow \dfrac{{{{\sin }^2}9^\circ  + {{\cos }^2}9^\circ }}{{\sin 9^\circ \cos 9^\circ }} - \left( {\dfrac{{{{\sin }^2}27^\circ  + {{\cos }^2}27^\circ }}{{\sin 27^\circ \cos 27^\circ }}} \right)$

We know that ${\sin ^2}\theta  + {\cos ^2}\theta  = 1$. Therefore, we get

\[ \Rightarrow \dfrac{1}{{\sin 9^\circ \cos 9^\circ }} - \dfrac{1}{{\sin 27^\circ \cos 27^\circ }}\]

Multiply and divide the expression by $2$ 

\[ \Rightarrow \dfrac{2}{{2\sin 9^\circ \cos 9^\circ }} - \dfrac{2}{{2\sin 27^\circ \cos 27^\circ }}\]

We know that $2\sin x\cos x = \sin 2x$. Therefore, we get

\[ \Rightarrow \dfrac{2}{{\sin 18^\circ }} - \dfrac{2}{{\sin 54^\circ }}\]

We know that $\sin 18^\circ  = \dfrac{{\sqrt 5  - 1}}{4}$ and $\sin 54^\circ  = \dfrac{{\sqrt 5  + 1}}{4}$. Therefore, we get

\[ \Rightarrow \dfrac{{2 \times 4}}{{\sqrt 5  - 1}} - \dfrac{{2 \times 4}}{{\sqrt 5  + 1}}\]

\[ \Rightarrow \dfrac{{8\left( {\sqrt 5  + 1} \right) - 8\left( {\sqrt 5  - 1} \right)}}{{5 - 1}}\]

\[ \Rightarrow \dfrac{{8\sqrt 5  + 8 - 8\sqrt 5  + 8}}{4}\]

\[ \Rightarrow \dfrac{{16}}{4}\]

\[ \Rightarrow 4\]

Example 6: Prove that $\dfrac{{\sec 8\theta  - 1}}{{\sec 4\theta  - 1}} = \dfrac{{\tan 8\theta }}{{\tan 2\theta }}$ 

Ans: We have, LHS $\dfrac{{\sec 8\theta  - 1}}{{\sec 4\theta  - 1}}$

Write the above-written expression in terms of $\cos ine$ 

$ \Rightarrow \dfrac{{\dfrac{1}{{\cos 8\theta }} - 1}}{{\dfrac{1}{{\cos 4\theta }} - 1}}$

$ \Rightarrow \dfrac{{\dfrac{{1 - \cos 8\theta }}{{\cos 8\theta }}}}{{\dfrac{{1 - \cos 4\theta }}{{\cos 4\theta }}}}$

$ \Rightarrow \dfrac{{1 - \cos 8\theta }}{{\cos 8\theta }} \times \dfrac{{\cos 4\theta }}{{1 - \cos 4\theta }}$

$ \Rightarrow \dfrac{{\left( {1 - \cos 8\theta } \right)\cos 4\theta }}{{\cos 8\theta \left( {1 - \cos 4\theta } \right)}}$

We know that $1 - \cos 2x = 2{\sin ^2}x$. Therefore, we get

$ \Rightarrow \dfrac{{2{{\sin }^2}4\theta \cos 4\theta }}{{\cos 8\theta 2{{\sin }^2}2\theta }}$

$ \Rightarrow \dfrac{{\sin 4\theta \left( {2\sin 4\theta \cos 4\theta } \right)}}{{2\cos 8\theta {{\sin }^2}2\theta }}$

We know that $2\sin x\cos x = \sin 2x$. Therefore, we get

$ \Rightarrow \dfrac{{\sin 4\theta \sin 8\theta }}{{2\cos 8\theta {{\sin }^2}2\theta }}$

We know that $2\sin x\cos x = \sin 2x$. Therefore, we get

$ \Rightarrow \dfrac{{2\sin 2\theta \cos 2\theta \sin 8\theta }}{{2\cos 8\theta {{\sin }^2}2\theta }}$

On canceling common terms, we get

$ \Rightarrow \dfrac{{\sin 8\theta \cos 2\theta }}{{\cos 8\theta \sin 2\theta }}$

$ \Rightarrow \dfrac{{\tan 8\theta }}{{\tan 2\theta }}$

Hence proved

Example 7: Solve the equation $\sin \theta  + \sin 3\theta  + \sin 5\theta  = 0$ 

Ans: We have, $\sin \theta  + \sin 3\theta  + \sin 5\theta  = 0$

$ \Rightarrow \left( {\sin 5\theta  + \sin \theta } \right) + \sin 3\theta  = 0$

We know that $\sin A + \sin B = 2\sin \dfrac{{A + B}}{2}\cos \dfrac{{A - B}}{2}$. Therefore, we get

$ \Rightarrow \left( {2\sin \dfrac{{5\theta  + \theta }}{2}\cos \dfrac{{5\theta  - \theta }}{2}} \right) + \sin 3\theta  = 0$

$ \Rightarrow 2\sin 3\theta \cos 2\theta  + \sin 3\theta  = 0$

$ \Rightarrow \sin 3\theta \left( {2\cos 2\theta  + 1} \right) = 0$

$ \Rightarrow \sin 3\theta  = 0$ or $2\cos 2\theta  + 1 = 0$

$ \Rightarrow \sin 3\theta  = 0$ or $\cos 2\theta  = \dfrac{{ - 1}}{2}$

Now, $\sin 3\theta  = 0$ 

$ \Rightarrow 3\theta  = n\pi ,n \in Z$

$ \Rightarrow \theta  = \dfrac{{n\pi }}{3},n \in Z$

And, $\cos 2\theta  = \dfrac{{ - 1}}{2}$

$ \Rightarrow \cos 2\theta  = \cos \left( {\pi  - \dfrac{\pi }{3}} \right)$

$ \Rightarrow \cos 2\theta  = \cos \left( {\dfrac{{3\pi  - \pi }}{3}} \right)$

$ \Rightarrow \cos 2\theta  = \cos \left( {\dfrac{{2\pi }}{3}} \right)$

We know that if $\cos \theta  = \cos \alpha $, then $\theta  = 2m\pi  \pm \alpha $. Therefore, we get

$ \Rightarrow 2\theta  = 2m\pi  \pm \dfrac{{2\pi }}{3},m \in Z$

$ \Rightarrow \theta  = m\pi  \pm \dfrac{\pi }{3},m \in Z$

Hence, the general solution of the given equation is $\theta  = \dfrac{{n\pi }}{3},n \in Z$ or, $\theta  = m\pi  \pm \dfrac{\pi }{3},m \in Z$.

Example 8: Solve $2{\tan ^2}x + {\sec ^2}x = 2$ for $0 \leqslant x \leqslant 2\pi $ 

Ans: We have, $2{\tan ^2}x + {\sec ^2}x = 2$

We know that ${\sec ^2}\theta  = 1 + {\tan ^2}\theta $. Therefore, we get

$ \Rightarrow 2{\tan ^2}x + 1 + {\tan ^2}x = 2$

$ \Rightarrow 3{\tan ^2}x = 2 - 1$

$ \Rightarrow 3{\tan ^2}x = 1$

$ \Rightarrow {\tan ^2}x = \dfrac{1}{3}$

$ \Rightarrow {\left( {\tan x} \right)^2} = {\left( {\dfrac{1}{{\sqrt 3 }}} \right)^2}$

$ \Rightarrow {\left( {\tan x} \right)^2} = {\left( {\tan \dfrac{\pi }{6}} \right)^2}$

$ \Rightarrow {\tan ^2}x = {\tan ^2}\dfrac{\pi }{6}$

We know that if ${\tan ^2}\theta  = {\tan ^2}\alpha $, then $\theta  = n\pi  \pm \alpha $, $n \in Z$.

$ \Rightarrow x = n\pi  \pm \dfrac{\pi }{6}$

Therefore, possible solutions are $\dfrac{\pi }{6}$, $\dfrac{{5\pi }}{6}$, $\dfrac{{7\pi }}{6}$, $\dfrac{{11\pi }}{6}$ where $0 \leqslant x \leqslant 2\pi $.

Long Answer Type

Example 9: Find the value of $\left( {1 + \cos \dfrac{\pi }{8}} \right)\left( {1 + \cos \dfrac{{3\pi }}{8}} \right)\left( {1 + \cos \dfrac{{5\pi }}{8}} \right)\left( {1 + \cos \dfrac{{7\pi }}{8}} \right)$ 

Ans: We have, $\left( {1 + \cos \dfrac{\pi }{8}} \right)\left( {1 + \cos \dfrac{{3\pi }}{8}} \right)\left( {1 + \cos \dfrac{{5\pi }}{8}} \right)\left( {1 + \cos \dfrac{{7\pi }}{8}} \right)$

$ \Rightarrow \left( {1 + \cos \dfrac{\pi }{8}} \right)\left( {1 + \cos \dfrac{{3\pi }}{8}} \right)\left( {1 + \cos \left( {\pi  - \dfrac{{3\pi }}{8}} \right)} \right)\left( {1 + \cos \left( {\pi  - \dfrac{\pi }{8}} \right)} \right)$

We know that $\cos \left( {\pi  - \theta } \right) =  - \cos \theta $. Therefore, we get

$ \Rightarrow \left( {1 + \cos \dfrac{\pi }{8}} \right)\left( {1 + \cos \dfrac{{3\pi }}{8}} \right)\left( {1 - \cos \dfrac{{3\pi }}{8}} \right)\left( {1 - \cos \dfrac{\pi }{8}} \right)$

$ \Rightarrow \left( {1 - {{\cos }^2}\dfrac{\pi }{8}} \right)\left( {1 - {{\cos }^2}\dfrac{{3\pi }}{8}} \right)$

We know that ${\sin ^2}\theta  = 1 - {\cos ^2}\theta $. Therefore, we get

$ \Rightarrow {\sin ^2}\dfrac{\pi }{8}{\sin ^2}\dfrac{{3\pi }}{8}$

Multiply and divide the above written expression by $4$.

$ \Rightarrow \dfrac{1}{4}\left( {2{{\sin }^2}\dfrac{\pi }{8}} \right)\left( {2{{\sin }^2}\dfrac{{3\pi }}{8}} \right)$

We know that $1 - \cos 2A = 2{\sin ^2}A$. Therefore, we get

$ \Rightarrow \dfrac{1}{4}\left( {1 - \cos \dfrac{\pi }{4}} \right)\left( {1 - \cos \dfrac{{3\pi }}{4}} \right)$

$ \Rightarrow \dfrac{1}{4}\left( {1 - \dfrac{1}{{\sqrt 2 }}} \right)\left( {1 + \dfrac{1}{{\sqrt 2 }}} \right)$

$ \Rightarrow \dfrac{1}{4}\left( {{1^2} - {{\left( {\dfrac{1}{{\sqrt 2 }}} \right)}^2}} \right)$

$ \Rightarrow \dfrac{1}{4}\left( {1 - \dfrac{1}{2}} \right)$

$ \Rightarrow \dfrac{1}{4}\left( {\dfrac{1}{2}} \right)$

$ \Rightarrow \dfrac{1}{8}$

Example 10: If $x\cos \theta  = y\cos \left( {\theta  + \dfrac{{2\pi }}{3}} \right) = z\cos \left( {\theta  + \dfrac{{4\pi }}{3}} \right)$, then find the value of $xy + yz + zx$ 

Ans: Note that $xy + yz + zx = xyz\left( {\dfrac{1}{x} + \dfrac{1}{y} + \dfrac{1}{z}} \right)$ 

Given that, $x\cos \theta  = y\cos \left( {\theta  + \dfrac{{2\pi }}{3}} \right) = z\cos \left( {\theta  + \dfrac{{4\pi }}{3}} \right)$

Let $x\cos \theta  = y\cos \left( {\theta  + \dfrac{{2\pi }}{3}} \right) = z\cos \left( {\theta  + \dfrac{{4\pi }}{3}} \right) = k$

Then, $x = \dfrac{k}{{\cos \theta }}$, $y = \dfrac{k}{{\cos \left( {\theta  + \dfrac{{2\pi }}{3}} \right)}}$ and $z = \dfrac{k}{{\cos \left( {\theta  + \dfrac{{4\pi }}{3}} \right)}}$ 

Now, we have 

$ \Rightarrow \dfrac{1}{x} + \dfrac{1}{y} + \dfrac{1}{z} = \dfrac{1}{{\dfrac{k}{{\cos \theta }}}} + \dfrac{1}{{\dfrac{k}{{\cos \left( {\theta  + \dfrac{{2\pi }}{3}} \right)}}}} + \dfrac{1}{{\dfrac{k}{{\cos \left( {\theta  + \dfrac{{4\pi }}{3}} \right)}}}}$ 

\[ \Rightarrow \dfrac{1}{x} + \dfrac{1}{y} + \dfrac{1}{z} = \dfrac{{\cos \theta }}{k} + \dfrac{{\cos \left( {\theta  + \dfrac{{2\pi }}{3}} \right)}}{k} + \dfrac{{\cos \left( {\theta  + \dfrac{{4\pi }}{3}} \right)}}{k}\]

\[ \Rightarrow \dfrac{1}{x} + \dfrac{1}{y} + \dfrac{1}{z} = \dfrac{1}{k}\left[ {\cos \theta  + \cos \left( {\theta  + \dfrac{{2\pi }}{3}} \right) + \cos \left( {\theta  + \dfrac{{4\pi }}{3}} \right)} \right]\]

We know that $\cos \left( {A + B} \right) = \cos A\cos B - \sin A\sin B$. Therefore, we get

\[ \Rightarrow \dfrac{1}{x} + \dfrac{1}{y} + \dfrac{1}{z} = \dfrac{1}{k}\left[ {\cos \theta  + \cos \theta \cos \dfrac{{2\pi }}{3} - \sin \theta \sin \dfrac{{2\pi }}{3} + \cos \theta \cos \dfrac{{4\pi }}{3} - \sin \theta \sin \dfrac{{4\pi }}{3}} \right]\]

\[ \Rightarrow \dfrac{1}{x} + \dfrac{1}{y} + \dfrac{1}{z} = \dfrac{1}{k}\left[ {\cos \theta  + \cos \theta \left( {\dfrac{{ - 1}}{2}} \right) - \sin \theta \left( {\dfrac{{\sqrt 3 }}{2}} \right) + \cos \theta \left( {\dfrac{{ - 1}}{2}} \right) - \sin \theta \left( {\dfrac{{ - \sqrt 3 }}{2}} \right)} \right]\]

\[ \Rightarrow \dfrac{1}{x} + \dfrac{1}{y} + \dfrac{1}{z} = \dfrac{1}{k}\left[ {\cos \theta  - \dfrac{1}{2}\cos \theta  - \dfrac{{\sqrt 3 }}{2}\sin \theta  - \dfrac{1}{2}\cos \theta  + \dfrac{{\sqrt 3 }}{2}\sin \theta } \right]\]

\[ \Rightarrow \dfrac{1}{x} + \dfrac{1}{y} + \dfrac{1}{z} = \dfrac{1}{k}\left[ {\cos \theta  - \cos \theta  - \dfrac{{\sqrt 3 }}{2}\sin \theta  + \dfrac{{\sqrt 3 }}{2}\sin \theta } \right]\]

\[ \Rightarrow \dfrac{1}{x} + \dfrac{1}{y} + \dfrac{1}{z} = \dfrac{1}{k}\left( 0 \right)\]

\[ \Rightarrow \dfrac{1}{x} + \dfrac{1}{y} + \dfrac{1}{z} = 0\]

$\therefore xy + yz + zx = xyz\left( 0 \right)$

$ \Rightarrow xy + yz + zx = 0$

Example 11: If $\alpha $ and $\beta $ are the solutions of the equation $a\tan \theta  + b\sec \theta  = c$, then show that $\tan \left( {\alpha  + \beta } \right) = \dfrac{{2ac}}{{{a^2} - {c^2}}}$.

Ans: Given that, $a\tan \theta  + b\sec \theta  = c$

Now, we will write the above written equation in terms of $\sin e$ and $\cos ine$.

$ \Rightarrow a\dfrac{{\sin \theta }}{{\cos \theta }} + b\dfrac{1}{{\cos \theta }} = c$

\[ \Rightarrow \dfrac{{a\sin \theta  + b}}{{\cos \theta }} = c\]

\[ \Rightarrow a\sin \theta  + b = c\cos \theta \]

We know that $\sin \theta  = \dfrac{{2\tan \dfrac{\theta }{2}}}{{1 + {{\tan }^2}\dfrac{\theta }{2}}}$ and $\cos \theta  = \dfrac{{1 - {{\tan }^2}\dfrac{\theta }{2}}}{{1 + {{\tan }^2}\dfrac{\theta }{2}}}$. Therefore, we get

\[ \Rightarrow \dfrac{{a\left( {2\tan \dfrac{\theta }{2}} \right)}}{{1 + {{\tan }^2}\dfrac{\theta }{2}}} + b = \dfrac{{c\left( {1 - {{\tan }^2}\dfrac{\theta }{2}} \right)}}{{1 + {{\tan }^2}\dfrac{\theta }{2}}}\]

\[ \Rightarrow \dfrac{{a\left( {2\tan \dfrac{\theta }{2}} \right) + b\left( {1 + {{\tan }^2}\dfrac{\theta }{2}} \right)}}{{1 + {{\tan }^2}\dfrac{\theta }{2}}} = \dfrac{{c\left( {1 - {{\tan }^2}\dfrac{\theta }{2}} \right)}}{{1 + {{\tan }^2}\dfrac{\theta }{2}}}\]

\[ \Rightarrow 2a\tan \dfrac{\theta }{2} + b\left( {1 + {{\tan }^2}\dfrac{\theta }{2}} \right) = c\left( {1 - {{\tan }^2}\dfrac{\theta }{2}} \right)\]

\[ \Rightarrow 2a\tan \dfrac{\theta }{2} + b + b{\tan ^2}\dfrac{\theta }{2} = c - c{\tan ^2}\dfrac{\theta }{2}\]

\[ \Rightarrow 2a\tan \dfrac{\theta }{2} + b{\tan ^2}\dfrac{\theta }{2} + c{\tan ^2}\dfrac{\theta }{2} + b - c = 0\]

\[ \Rightarrow \left( {b + c} \right){\tan ^2}\dfrac{\theta }{2} + 2a\tan \dfrac{\theta }{2} + b - c = 0\]

Above written equation is quadratic in $\tan \dfrac{\theta }{2}$ and hence $\tan \dfrac{\alpha }{2}$ and $\tan \dfrac{\beta }{2}$ are the roots of this equation.

We know that if the roots of the quadratic equation $a{x^2} + bx + c = 0$ are $\alpha $ and $\beta $. Then we have, $\alpha  + \beta  =  - \dfrac{b}{a}$ and $\alpha \beta  = \dfrac{c}{a}$. Therefore, we get

$ \Rightarrow \tan \dfrac{\alpha }{2} + \tan \dfrac{\beta }{2} = \dfrac{{ - 2a}}{{b + c}}$ and $\tan \dfrac{\alpha }{2}\tan \dfrac{\beta }{2} = \dfrac{{b - c}}{{b + c}}$ 

We know that $\tan \left( {x + y} \right) = \dfrac{{\tan x + \tan y}}{{1 - \tan x\tan y}}$. Therefore, we get

$ \Rightarrow \tan \left( {\dfrac{\alpha }{2} + \dfrac{\beta }{2}} \right) = \dfrac{{\tan \dfrac{\alpha }{2} + \tan \dfrac{\beta }{2}}}{{1 - \tan \dfrac{\alpha }{2}\tan \dfrac{\beta }{2}}}$

On substituting the values, we get

$ \Rightarrow \tan \left( {\dfrac{\alpha }{2} + \dfrac{\beta }{2}} \right) = \dfrac{{\dfrac{{ - 2a}}{{b + c}}}}{{1 - \left( {\dfrac{{b - c}}{{b + c}}} \right)}}$

$ \Rightarrow \tan \left( {\dfrac{\alpha }{2} + \dfrac{\beta }{2}} \right) = \dfrac{{\dfrac{{ - 2a}}{{b + c}}}}{{\dfrac{{b + c - b + c}}{{b + c}}}}$

$ \Rightarrow \tan \left( {\dfrac{\alpha }{2} + \dfrac{\beta }{2}} \right) = \dfrac{{ - 2a}}{{2c}}$

$ \Rightarrow \tan \left( {\dfrac{{\alpha  + \beta }}{2}} \right) = \dfrac{{ - a}}{c}......\left( i \right)$

We know that $\tan 2x = \dfrac{{2\tan x}}{{1 - {{\tan }^2}x}}$. Thus, we have

$ \Rightarrow \tan 2\left( {\dfrac{{\alpha  + \beta }}{2}} \right) = \dfrac{{2\tan \left( {\dfrac{{\alpha  + \beta }}{2}} \right)}}{{1 - {{\tan }^2}\left( {\dfrac{{\alpha  + \beta }}{2}} \right)}}$

On substituting the values, we get

$ \Rightarrow \tan \left( {\alpha  + \beta } \right) = \dfrac{{2\left( {\dfrac{{ - a}}{c}} \right)}}{{1 - {{\left( {\dfrac{{ - a}}{c}} \right)}^2}}}$

$ \Rightarrow \tan \left( {\alpha  + \beta } \right) = \dfrac{{\dfrac{{ - 2a}}{c}}}{{\dfrac{{{c^2} - {a^2}}}{{{c^2}}}}}$

$ \Rightarrow \tan \left( {\alpha  + \beta } \right) = \dfrac{{ - 2a}}{c} \times \dfrac{{{c^2}}}{{{c^2} - {a^2}}}$

$ \Rightarrow \tan \left( {\alpha  + \beta } \right) = \dfrac{{ - 2ac}}{{{c^2} - {a^2}}}$

$ \Rightarrow \tan \left( {\alpha  + \beta } \right) = \dfrac{{2ac}}{{{a^2} - {c^2}}}$

Hence proved

Example 12: Show that $2{\sin ^2}\beta  + 4\cos \left( {\alpha  + \beta } \right)\sin \alpha \sin \beta  + \cos 2\left( {\alpha  + \beta } \right) = \cos 2\alpha $ 

Ans: We have LHS, $2{\sin ^2}\beta  + 4\cos \left( {\alpha  + \beta } \right)\sin \alpha \sin \beta  + \cos 2\left( {\alpha  + \beta } \right)$

$2{\sin ^2}\beta  + 4\cos \left( {\alpha  + \beta } \right)\sin \alpha \sin \beta  + \cos \left( {2\alpha  + 2\beta } \right)$

We know that $\cos \left( {A + B} \right) = \cos A\cos B - \sin A\sin B$. Therefore, we get

$ \Rightarrow 2{\sin ^2}\beta  + 4\left( {\cos \alpha \cos \beta  - \sin \alpha \sin \beta } \right)\sin \alpha \sin \beta  + \left( {\cos 2\alpha \cos 2\beta  - \sin 2\alpha \sin 2\beta } \right)$

\[ \Rightarrow 2{\sin ^2}\beta  + 4\sin \alpha \cos \alpha \sin \beta \cos \beta  - 4{\sin ^2}\alpha {\sin ^2}\beta  + \cos 2\alpha \cos 2\beta  - \sin 2\alpha \sin 2\beta \]

We know that $2\sin x\cos x = \sin 2x$. Therefore, we get

\[ \Rightarrow 2{\sin ^2}\beta  + \sin 2\alpha \sin 2\beta  - 4{\sin ^2}\alpha {\sin ^2}\beta  + \cos 2\alpha \cos 2\beta  - \sin 2\alpha \sin 2\beta \]

\[ \Rightarrow 2{\sin ^2}\beta  - 4{\sin ^2}\alpha {\sin ^2}\beta  + \cos 2\alpha \cos 2\beta \]

We can also the above written expression as,

\[ \Rightarrow 2{\sin ^2}\beta  - \left( {2{{\sin }^2}\alpha } \right)\left( {2{{\sin }^2}\beta } \right) + \cos 2\alpha \cos 2\beta \]

We know that $2{\sin ^2}A = 1 - \cos 2A$. Therefore, we get

\[ \Rightarrow \left( {1 - \cos 2\beta } \right) - \left( {1 - \cos 2\alpha } \right)\left( {1 - \cos 2\beta } \right) + \cos 2\alpha \cos 2\beta \]

\[ \Rightarrow 1 - \cos 2\beta  - \left( {1 - \cos 2\beta  - \cos 2\alpha  + \cos 2\beta \cos 2\alpha } \right) + \cos 2\alpha \cos 2\beta \]

\[ \Rightarrow 1 - \cos 2\beta  - 1 + \cos 2\beta  + \cos 2\alpha  - \cos 2\beta \cos 2\alpha  + \cos 2\alpha \cos 2\beta \]

$ \Rightarrow \cos 2\alpha $ 

Hence proved

Example 13: If an angle $\theta $ is divided into two parts such that the tangent of one part is $k$ times the tangent of other, and $\phi $ is their difference, then show that $\sin \theta  = \dfrac{{k + 1}}{{k - 1}}\sin \phi $.

Ans: Let $\theta  = \alpha  + \beta $. Then $\tan \alpha  = k\tan \beta $.

$ \Rightarrow \dfrac{{\tan \alpha }}{{\tan \beta }} = \dfrac{k}{1}$ 

Now, we will apply componendo and dividend 

$ \Rightarrow \dfrac{{\tan \alpha  + \tan \beta }}{{\tan \alpha  - \tan \beta }} = \dfrac{{k + 1}}{{k - 1}}$

Now, we will write the above written expression in terms of $\sin e$ and $\cos ine$ 

$ \Rightarrow \dfrac{{\dfrac{{\sin \alpha }}{{\cos \alpha }} + \dfrac{{\sin \beta }}{{\cos \beta }}}}{{\dfrac{{\sin \alpha }}{{\cos \alpha }} - \dfrac{{\sin \beta }}{{\cos \beta }}}} = \dfrac{{k + 1}}{{k - 1}}$

$ \Rightarrow \dfrac{{\dfrac{{\sin \alpha \cos \beta  + \cos \alpha \sin \beta }}{{\cos \alpha \cos \beta }}}}{{\dfrac{{\sin \alpha \cos \beta  - \cos \alpha \sin \beta }}{{\cos \alpha \cos \beta }}}} = \dfrac{{k + 1}}{{k - 1}}$

$ \Rightarrow \dfrac{{\sin \alpha \cos \beta  + \cos \alpha \sin \beta }}{{\sin \alpha \cos \beta  - \cos \alpha \sin \beta }} = \dfrac{{k + 1}}{{k - 1}}$

We know that $\sin \left( {A + B} \right) = \sin A\cos B + \cos A\sin B$ and $\sin \left( {A - B} \right) = \sin A\cos B - \cos A\sin B$. Therefore, we get

$ \Rightarrow \dfrac{{\sin \left( {\alpha  + \beta } \right)}}{{\sin \left( {\alpha  - \beta } \right)}} = \dfrac{{k + 1}}{{k - 1}}$

Given that, $\alpha  - \beta  = \phi $ and $\alpha  + \beta  = \theta $. Therefore, we get

$ \Rightarrow \dfrac{{\sin \theta }}{{\sin \phi }} = \dfrac{{k + 1}}{{k - 1}}$

$ \Rightarrow \sin \theta  = \dfrac{{k + 1}}{{k - 1}}\sin \phi $

Hence proved

Example 14: Solve $\sqrt 3 \cos \theta  + \sin \theta  = \sqrt 2 $.

Ans: We have equation, $\sqrt 3 \cos \theta  + \sin \theta  = \sqrt 2 $

Divide the equation by $2$ 

$ \Rightarrow \dfrac{{\sqrt 3 }}{2}\cos \theta  + \dfrac{1}{2}\sin \theta  = \dfrac{{\sqrt 2 }}{2}$

$ \Rightarrow \dfrac{{\sqrt 3 }}{2}\cos \theta  + \dfrac{1}{2}\sin \theta  = \dfrac{1}{{\sqrt 2 }}$

We know that $\cos \dfrac{\pi }{6} = \dfrac{{\sqrt 3 }}{2}$, $\cos \dfrac{\pi }{4} = \dfrac{1}{{\sqrt 2 }}$and $\sin \dfrac{\pi }{6} = \dfrac{1}{2}$. So, we can written above-written equation as

$ \Rightarrow \cos \dfrac{\pi }{6}\cos \theta  + \sin \dfrac{\pi }{6}\sin \theta  = \cos \dfrac{\pi }{4}$

$ \Leftrightarrow \cos \theta \cos \dfrac{\pi }{6} + \sin \theta \sin \dfrac{\pi }{6} = \cos \dfrac{\pi }{4}$

We know that $\cos \left( {x - y} \right) = \cos x\cos y + \sin x\sin y$. Therefore, we get

$ \Rightarrow \cos \left( {\theta  - \dfrac{\pi }{6}} \right) = \cos \dfrac{\pi }{4}$

We know that when $\cos \theta  = \cos \alpha $, then $\theta  = 2n\pi  \pm \alpha $, where $n \in Z$.

$ \Rightarrow \theta  - \dfrac{\pi }{6} = 2n\pi  \pm \dfrac{\pi }{4}$

$ \Rightarrow \theta  = 2n\pi  \pm \dfrac{\pi }{4} + \dfrac{\pi }{6}$

Hence, the solutions are $\theta  = 2n\pi  + \dfrac{\pi }{4} + \dfrac{\pi }{6}$ and $\theta  = 2n\pi  - \dfrac{\pi }{4} + \dfrac{\pi }{6}$

i.e., $\theta  = 2n\pi  + \dfrac{{5\pi }}{{12}}$ and $\theta  = 2n\pi  - \dfrac{\pi }{{12}}$

Objective Type Questions

Choose the correct answer from the given four options against each of the examples $15$ to $19$.

Example 15: If $\tan \theta  = \dfrac{{ - 4}}{3}$, then $\sin \theta $ is

a) $\dfrac{{ - 4}}{5}$ but not $\dfrac{4}{5}$

 b) $\dfrac{{ - 4}}{5}$ or $\dfrac{4}{5}$

c) $\dfrac{4}{5}$ but not $\dfrac{{ - 4}}{5}$

d) None of these

Ans: The correct answer is option (b) $\dfrac{{ - 4}}{5}$ or $\dfrac{4}{5}$

Given that, $\tan \theta  = \dfrac{{ - 4}}{3} = \dfrac{P}{B}$.

By Pythagoras theorem, we have

$ \Rightarrow {H^2} = {P^2} + {B^2}$ 

$ \Rightarrow {H^2} = {4^2} + {3^2}$

(Here, we have taken positive value of perpendicular because length can’t be negative)

$ \Rightarrow {H^2} = 16 + 9$

$ \Rightarrow {H^2} = 25$

$ \Rightarrow H = 5$

Since $\tan \theta  = \dfrac{{ - 4}}{3}$ is negative, $\theta $ lies either in second quadrant or in fourth quadrant. 

We know that $\sin \theta  = \dfrac{P}{H}$. Therefore, we get

If $\theta $ lies in second quadrant, $\sin \theta  = \dfrac{4}{5}$ and if $\theta $ lies in fourth quadrant, $\sin \theta  =  - \dfrac{4}{5}$.

Hence, the required answer is (b) $\dfrac{{ - 4}}{5}$ or $\dfrac{4}{5}$

Example 16: If $\sin \theta $ and $\cos \theta $ are the roots of the equation $a{x^2} - bx + c = 0$, then $a$, $b$ and $c$ satisfy the relation.

a) ${a^2} + {b^2} + 2ac = 0$

b) ${a^2} - {b^2} + 2ac = 0$

c) ${a^2} + {c^2} + 2ab = 0$

d) \[{a^2} - {b^2} - 2ac = 0\]

Ans: The correct answer is option (b) ${a^2} - {b^2} + 2ac = 0$

Given that, $\sin \theta $ and $\cos \theta $ are the roots of the equation $a{x^2} - bx + c = 0$.

We know that if the roots of the quadratic equation $a{x^2} + bx + c = 0$ are $\alpha $ and $\beta $. Then we have, $\alpha  + \beta  =  - \dfrac{b}{a}$ and $\alpha \beta  = \dfrac{c}{a}$. Therefore, we get

$ \Rightarrow \sin \theta  + \cos \theta  = \dfrac{b}{a}...\left( i \right)$ and $\sin \theta \cos \theta  = \dfrac{c}{a}.....\left( {ii} \right)$

On squaring both the sides in equation $\left( i \right)$, we get

$ \Rightarrow {\sin ^2}\theta  + {\cos ^2}\theta  + 2\sin \theta \cos \theta  = \dfrac{{{b^2}}}{{{a^2}}}$

We have, $\sin \theta \cos \theta  = \dfrac{c}{a}$ and we know that ${\sin ^2}\theta  + {\cos ^2}\theta  = 1$. Therefore, we get

$ \Rightarrow 1 + \dfrac{{2c}}{a} = \dfrac{{{b^2}}}{{{a^2}}}$

$ \Rightarrow \dfrac{{a + 2c}}{a} = \dfrac{{{b^2}}}{{{a^2}}}$

$ \Rightarrow \dfrac{{a + 2c}}{1} = \dfrac{{{b^2}}}{a}$

On cross multiplication, we get

$ \Rightarrow {a^2} + 2ac = {b^2}$

$ \Rightarrow {a^2} - {b^2} + 2ac = 0$

Example 17: The greatest value of $\sin x\cos x$ is

a) $1$

b) $2$

c) $\sqrt 2 $

d) \[\dfrac{1}{2}\]

Ans: The correct answer is option (d) $\dfrac{1}{2}$ 

We have, $\sin x\cos x$

Multiply and divide the expression by $2$  

$ \Rightarrow \dfrac{1}{2} \times 2\sin x\cos x$

We know that $2\sin x\cos x = \sin 2x$. Therefore, we get

\[ \Rightarrow \dfrac{1}{2} \times \sin 2x\]

We know that, 

$ \Rightarrow  - 1 \leqslant \sin 2x \leqslant 1$ 

Divide the expression by $2$ 

$ \Rightarrow  - \dfrac{1}{2} \leqslant \dfrac{{\sin 2x}}{2} \leqslant \dfrac{1}{2}$

Hence, the greatest is $\dfrac{1}{2}$.

Example 18: The value of $\sin 20^\circ \sin 40^\circ \sin 60^\circ \sin 80^\circ $ is

a) $\dfrac{{ - 3}}{{16}}$

b) $\dfrac{5}{{16}}$

c) $\dfrac{3}{{16}}$

d) $\dfrac{1}{{16}}$

Ans: The correct answer is option (c) $\dfrac{3}{{16}}$

$ \Rightarrow \sin 60^\circ \sin 20^\circ \sin 40^\circ \sin 80^\circ $

We know that $\sin 60^\circ  = \dfrac{{\sqrt 3 }}{2}$. Therefore, we get

$ \Rightarrow \dfrac{{\sqrt 3 }}{2}\sin 20^\circ \left( {\sin 40^\circ \sin 80^\circ } \right)$

Multiply and divide the expression by $2$.

$ \Rightarrow \dfrac{{\sqrt 3 }}{2} \times \dfrac{1}{2}\sin 20^\circ \left( {2\sin 80^\circ \sin 40^\circ } \right)$

We know that $2\sin A\sin B = \cos \left( {A - B} \right) - \cos \left( {A + B} \right)$. Therefore, we get

$ \Rightarrow \dfrac{{\sqrt 3 }}{4}\sin 20^\circ \left( {\cos 40^\circ  - \cos 120^\circ } \right)$

$ \Rightarrow \dfrac{{\sqrt 3 }}{4}\left[ {\sin 20^\circ \cos 40^\circ  - \sin 20^\circ \cos 120^\circ } \right]$

We know that $\cos 120^\circ  =  - \dfrac{1}{2}$. Therefore, we get

$ \Rightarrow \dfrac{{\sqrt 3 }}{4}\left[ {\sin 20^\circ \cos 40^\circ  - \sin 20^\circ \left( { - \dfrac{1}{2}} \right)} \right]$

Multiply and divide the expression by $2$ 

$ \Rightarrow \dfrac{{\sqrt 3 }}{{4 \times 2}}\left[ {2\sin 20^\circ \cos 40^\circ  - 2\sin 20^\circ \left( { - \dfrac{1}{2}} \right)} \right]$

$ \Rightarrow \dfrac{{\sqrt 3 }}{8}\left[ {2\sin 20^\circ \cos 40^\circ  + \sin 20^\circ } \right]$

We know that $2\sin A\cos B = \sin \left( {A + B} \right) + \sin \left( {A - B} \right)$. Therefore, we get

$ \Rightarrow \dfrac{{\sqrt 3 }}{8}\left[ {\sin 60^\circ  + \sin \left( { - 20^\circ } \right) + \sin 20^\circ } \right]$

We know that $\sin \left( { - \theta } \right) =  - \sin \theta $. Therefore, we get

$ \Rightarrow \dfrac{{\sqrt 3 }}{8}\left( {\dfrac{{\sqrt 3 }}{2}} \right)$

$ \Rightarrow \dfrac{3}{{16}}$

Example 19: The value of $\cos \dfrac{\pi }{5}\cos \dfrac{{2\pi }}{5}\cos \dfrac{{4\pi }}{5}\cos \dfrac{{8\pi }}{5}$ is

a) $\dfrac{1}{{16}}$

b) $0$

c) $\dfrac{{ - 1}}{8}$

d) $\dfrac{{ - 1}}{{16}}$

Ans: The correct answer is option (d) $\dfrac{{ - 1}}{{16}}$ 

We have, $\cos \dfrac{\pi }{5}\cos \dfrac{{2\pi }}{5}\cos \dfrac{{4\pi }}{5}\cos \dfrac{{8\pi }}{5}$

Multiply the above-written expression by $2\sin \dfrac{\pi }{5}$.

$ \Rightarrow \dfrac{1}{{2\sin \dfrac{\pi }{5}}}2\sin \dfrac{\pi }{5}\cos \dfrac{\pi }{5}\cos \dfrac{{2\pi }}{5}\cos \dfrac{{4\pi }}{5}\cos \dfrac{{8\pi }}{5}$

We know that $2\sin x\cos x = \sin 2x$. Therefore, we get

$ \Rightarrow \dfrac{1}{{2\sin \dfrac{\pi }{5}}}\sin \dfrac{{2\pi }}{5}\cos \dfrac{{2\pi }}{5}\cos \dfrac{{4\pi }}{5}\cos \dfrac{{8\pi }}{5}$

Multiply and divide the expression by $2$ 

$ \Rightarrow \dfrac{1}{{2 \times 2\sin \dfrac{\pi }{5}}}2\sin \dfrac{{2\pi }}{5}\cos \dfrac{{2\pi }}{5}\cos \dfrac{{4\pi }}{5}\cos \dfrac{{8\pi }}{5}$

We know that $2\sin x\cos x = \sin 2x$. Therefore, we get

$ \Rightarrow \dfrac{1}{{4\sin \dfrac{\pi }{5}}}\sin \dfrac{{4\pi }}{5}\cos \dfrac{{4\pi }}{5}\cos \dfrac{{8\pi }}{5}$

Multiply and divide the expression by $2$ 

$ \Rightarrow \dfrac{1}{{2 \times 4\sin \dfrac{\pi }{5}}}2\sin \dfrac{{4\pi }}{5}\cos \dfrac{{4\pi }}{5}\cos \dfrac{{8\pi }}{5}$

$ \Rightarrow \dfrac{1}{{8\sin \dfrac{\pi }{5}}}\sin \dfrac{{8\pi }}{5}\cos \dfrac{{8\pi }}{5}$

Multiply and divide the expression by $2$ 

$ \Rightarrow \dfrac{1}{{2 \times 8\sin \dfrac{\pi }{5}}}2\sin \dfrac{{8\pi }}{5}\cos \dfrac{{8\pi }}{5}$

$ \Rightarrow \dfrac{1}{{16\sin \dfrac{\pi }{5}}}\sin \dfrac{{16\pi }}{5}$

$ \Rightarrow \dfrac{{\sin \left( {3\pi  + \dfrac{\pi }{5}} \right)}}{{16\sin \dfrac{\pi }{5}}}$

$ \Rightarrow \dfrac{{ - \sin \dfrac{\pi }{5}}}{{16\sin \dfrac{\pi }{5}}}$

$ \Rightarrow \dfrac{{ - 1}}{{16}}$

Fill in the blank:

Example 20: If $3\tan \left( {\theta  - 15^\circ } \right) = \tan \left( {\theta  + 15^\circ } \right)$, $0^\circ  < \theta  < 90^\circ $, then $\theta $ = _____.

Ans: Given that, $3\tan \left( {\theta  - 15^\circ } \right) = \tan \left( {\theta  + 15^\circ } \right)$

$ \Rightarrow \dfrac{{\tan \left( {\theta  + 15^\circ } \right)}}{{\tan \left( {\theta  - 15^\circ } \right)}} = \dfrac{3}{1}$

Now, we will apply componendo and dividendo rule. Therefore, we get

$ \Rightarrow \dfrac{{\tan \left( {\theta  + 15^\circ } \right) + \tan \left( {\theta  - 15^\circ } \right)}}{{\tan \left( {\theta  + 15^\circ } \right) - \tan \left( {\theta  - 15^\circ } \right)}} = \dfrac{{3 + 1}}{{3 - 1}}$

$ \Rightarrow \dfrac{{\dfrac{{\sin \left( {\theta  + 15^\circ } \right)}}{{\cos \left( {\theta  + 15^\circ } \right)}} + \dfrac{{\sin \left( {\theta  - 15^\circ } \right)}}{{\cos \left( {\theta  - 15^\circ } \right)}}}}{{\dfrac{{\sin \left( {\theta  + 15^\circ } \right)}}{{\cos \left( {\theta  + 15^\circ } \right)}} - \dfrac{{\sin \left( {\theta  - 15^\circ } \right)}}{{\cos \left( {\theta  - 15^\circ } \right)}}}} = \dfrac{4}{2}$

$ \Rightarrow \dfrac{{\dfrac{{\sin \left( {\theta  + 15^\circ } \right)\cos \left( {\theta  - 15^\circ } \right) + \sin \left( {\theta  - 15^\circ } \right)\cos \left( {\theta  + 15^\circ } \right)}}{{\cos \left( {\theta  + 15^\circ } \right)\cos \left( {\theta  - 15^\circ } \right)}}}}{{\dfrac{{\sin \left( {\theta  + 15^\circ } \right)\cos \left( {\theta  - 15^\circ } \right) - \sin \left( {\theta  - 15^\circ } \right)\cos \left( {\theta  + 15^\circ } \right)}}{{\cos \left( {\theta  + 15^\circ } \right)\cos \left( {\theta  - 15^\circ } \right)}}}} = 2$

$ \Rightarrow \dfrac{{\sin \left( {\theta  + 15^\circ } \right)\cos \left( {\theta  - 15^\circ } \right) + \sin \left( {\theta  - 15^\circ } \right)\cos \left( {\theta  + 15^\circ } \right)}}{{\sin \left( {\theta  + 15^\circ } \right)\cos \left( {\theta  - 15^\circ } \right) - \sin \left( {\theta  - 15^\circ } \right)\cos \left( {\theta  + 15^\circ } \right)}} = 2$

We know that $\sin \left( {A + B} \right) = \sin A\cos B + \cos A\sin B$ and $\sin \left( {A - B} \right) = \sin A\cos B - \cos A\sin B$. Therefore, we get

$ \Rightarrow \dfrac{{\sin \left( {\theta  + 15^\circ  + \theta  - 15^\circ } \right)}}{{\sin \left( {\theta  + 15^\circ  - \left( {\theta  - 15^\circ } \right)} \right)}} = 2$

$ \Rightarrow \dfrac{{\sin 2\theta }}{{\sin \left( {\theta  + 15^\circ  - \theta  + 15^\circ } \right)}} = 2$

$ \Rightarrow \dfrac{{\sin 2\theta }}{{\sin 30^\circ }} = 2$

We know that $\sin 30^\circ  = \dfrac{1}{2}$. Therefore, we get

$ \Rightarrow \dfrac{{\sin 2\theta }}{{\dfrac{1}{2}}} = 2$

$ \Rightarrow \dfrac{{2\sin 2\theta }}{1} = 2$

$ \Rightarrow \sin 2\theta  = 1$

Given that, $0^\circ  < \theta  < 90^\circ $ i.e., $0 < \theta  < \dfrac{\pi }{2}$ 

$\therefore 0 < 2\theta  < \pi $

$ \Rightarrow \sin 2\theta  = \sin \dfrac{\pi }{2}$ 

$ \Rightarrow 2\theta  = \dfrac{\pi }{2}$

$ \Rightarrow \theta  = \dfrac{\pi }{4}$

Or 

$ \Rightarrow \theta  = 45^\circ $

State whether the following statement is true or false. Justify your answer.

Example 21: “The inequality ${2^{\sin \theta }} + {2^{\cos \theta }} \geqslant {2^{1 - \dfrac{1}{{\sqrt 2 }}}}$ holds for all real values of $\theta $ ”.

Ans: The given statement is true.

Since, ${2^{\sin \theta }}$ and ${2^{\cos \theta }}$ are positive real numbers, so arithmetic mean of these two numbers is greater or equal to their geometric mean.

$ \Rightarrow \dfrac{{{2^{\sin \theta }} + {2^{\cos \theta }}}}{2} \geqslant \sqrt {{2^{\sin \theta }} \times {2^{\cos \theta }}} $

$ \Rightarrow {2^{\sin \theta }} + {2^{\cos \theta }} \geqslant 2\sqrt {{2^{\sin \theta  + \cos \theta }}} $

$ \Rightarrow {2^{\sin \theta }} + {2^{\cos \theta }} \geqslant {2.2^{\dfrac{{\sin \theta  + \cos \theta }}{2}}}......\left( i \right)$

We have, $\sin \theta  + \cos \theta $.

Divide and multiply the expression by $\sqrt 2 $ 

$ \Rightarrow \sqrt 2 \left( {\sin \theta  \times \dfrac{1}{{\sqrt 2 }} + \cos \theta  \times \dfrac{1}{{\sqrt 2 }}} \right)$ 

We know that $\sin \dfrac{\pi }{4} = \dfrac{1}{{\sqrt 2 }}$ and $\cos \dfrac{\pi }{4} = \dfrac{1}{{\sqrt 2 }}$. Therefore, we get

$ \Rightarrow \sqrt 2 \left( {\sin \theta \cos \dfrac{\pi }{4} + \cos \theta \sin \dfrac{\pi }{4}} \right)$

We know that $\sin \left( {x + y} \right) = \sin x\cos y + \cos x\sin y$. Therefore, we get

$ \Rightarrow \sqrt 2 \sin \left( {\theta  + \dfrac{\pi }{4}} \right)$

Since, $ - 1 \leqslant \sin \left( {\theta  + \dfrac{\pi }{4}} \right) \leqslant 1$

$ \Rightarrow  - \sqrt 2  \leqslant \sqrt 2 \sin \left( {\theta  + \dfrac{\pi }{4}} \right) \leqslant \sqrt 2 $

As we solved above, $\sin \theta  + \cos \theta  = \sqrt 2 \sin \left( {\theta  + \dfrac{\pi }{4}} \right)$. Therefore, we get

$ \Rightarrow  - \sqrt 2  \leqslant \sin \theta  + \cos \theta  \leqslant \sqrt 2 $

$ \Rightarrow  - \dfrac{{\sqrt 2 }}{2} \leqslant \dfrac{{\sin \theta  + \cos \theta }}{2} \leqslant \dfrac{{\sqrt 2 }}{2}$

$ \Rightarrow  - \dfrac{1}{{\sqrt 2 }} \leqslant \dfrac{{\sin \theta  + \cos \theta }}{2} \leqslant \dfrac{1}{{\sqrt 2 }}$

We have, ${2^{\sin \theta }} + {2^{\cos \theta }} \geqslant {2.2^{\dfrac{{\sin \theta  + \cos \theta }}{2}}}......\left( i \right)$

$ \Rightarrow {2^{\sin \theta }} + {2^{\cos \theta }} \geqslant {2.2^{\dfrac{{ - 1}}{{\sqrt 2 }}}}$

$ \Rightarrow {2^{\sin \theta }} + {2^{\cos \theta }} \geqslant {2^{1 + \left( {\dfrac{{ - 1}}{{\sqrt 2 }}} \right)}}$

\[ \Rightarrow {2^{\sin \theta }} + {2^{\cos \theta }} \geqslant {2^{1 - \dfrac{1}{{\sqrt 2 }}}}\]

State whether the following statement is true or false. Justify your answer.

Example 22: Match each item given under the column ${C_1}$ to its correct answer given under the column ${C_2}$.       

         ${C_1}$                                                                            ${C_2}$                                                 

a) $\dfrac{{1 - \cos x}}{{\sin x}}$                                                                 (i) ${\cot ^2}\dfrac{x}{2}$      

b) $\dfrac{{1 + \cos x}}{{1 - \cos x}}$                                                                 (ii) $\cot \dfrac{x}{2}$

c) $\dfrac{{1 + \cos x}}{{\sin x}}$                                                                  (iii) $\left| {\cos x + \sin x} \right|$

d) $\sqrt {1 + \sin 2x} $                                                              (iv) $\tan \dfrac{x}{2}$

Ans: 

a) $\dfrac{{1 - \cos x}}{{\sin x}}$         

We know that $1 - \cos 2A = 2{\sin ^2}A$ and $\sin 2A = 2\sin A\cos A$. Therefore, we get

 $ \Rightarrow \dfrac{{2{{\sin }^2}\dfrac{x}{2}}}{{2\sin \dfrac{x}{2}\cos \dfrac{x}{2}}}$

$ \Rightarrow \dfrac{{\sin \dfrac{x}{2}}}{{\cos \dfrac{x}{2}}}$

$ \Rightarrow \tan \dfrac{x}{2}$

Hence, $\left( a \right) \leftrightarrow \left( {iv} \right)$.

b) $\dfrac{{1 + \cos x}}{{1 - \cos x}}$

We know that $1 + \cos 2A = 2{\cos ^2}A$ and $1 - \cos 2A = 2{\sin ^2}A$. Therefore, we get

$ \Rightarrow \dfrac{{2{{\cos }^2}\dfrac{x}{2}}}{{2{{\sin }^2}\dfrac{x}{2}}}$

$ \Rightarrow {\cot ^2}\dfrac{x}{2}$

Hence, $\left( b \right) \leftrightarrow \left( i \right)$.

c) $\dfrac{{1 + \cos x}}{{\sin x}}$

We know that $1 + \cos 2A = 2{\cos ^2}A$ and $\sin 2A = 2\sin A\cos A$. Therefore, we get

$ \Rightarrow \dfrac{{2{{\cos }^2}\dfrac{x}{2}}}{{2\sin \dfrac{x}{2}\cos \dfrac{x}{2}}}$

$ \Rightarrow \dfrac{{\cos \dfrac{x}{2}}}{{\sin \dfrac{x}{2}}}$

$ \Rightarrow \cot \dfrac{x}{2}$

Hence, $\left( c \right) \leftrightarrow \left( {ii} \right)$

d) $\sqrt {1 + \sin 2x} $

We know that ${\sin ^2}A + {\cos ^2}A = 1$ and $\sin 2A = 2\sin A\cos A$. Therefore, we get

$ \Rightarrow \sqrt {{{\sin }^2}x + {{\cos }^2}x + 2\sin x\cos x} $

$ \Rightarrow \sqrt {{{\left( {\sin x + \cos x} \right)}^2}} $

$ \Rightarrow \left| {\left( {\sin x + \cos x} \right)} \right|$

$ \Rightarrow \left| {\cos x + \sin x} \right|$ 

Hence, $\left( d \right) \leftrightarrow \left( {iii} \right)$.

Exercise 3.3

Short Answer Type

1. Prove that $\dfrac{{\tan A + \sec A - 1}}{{\tan A - \sec A + 1}} = \dfrac{{1 + \sin A}}{{\cos A}}$.

Ans: We need to prove that $\dfrac{{\tan A + \sec A - 1}}{{\tan A - \sec A + 1}} = \dfrac{{1 + \sin A}}{{\cos A}}$

L.H.S. = $\dfrac{{\tan A + \sec A - 1}}{{\tan A - \sec A + 1}}$

We know that ${\sec ^2}A - {\tan ^2}A = 1$. Therefore, we get

$ \Rightarrow \dfrac{{\tan A + \sec A - \left( {{{\sec }^2}A - {{\tan }^2}A} \right)}}{{\tan A - \sec A + 1}}$

We know that ${a^2} - {b^2} = \left( {a + b} \right)\left( {a - b} \right)$. Therefore, we get

$ \Rightarrow \dfrac{{\tan A + \sec A - \left[ {\left( {\sec A + \tan A} \right)\left( {\sec A - \tan A} \right)} \right]}}{{\tan A - \sec A + 1}}$

Take $\sec A + \tan A$ as a common term

$ \Rightarrow \dfrac{{\left( {\sec A + \tan A} \right)\left[ {1 - \left( {\sec A - \tan A} \right)} \right]}}{{\tan A - \sec A + 1}}$

\[ \Rightarrow \dfrac{{\left( {\sec A + \tan A} \right)\left[ {1 - \sec A + \tan A} \right]}}{{\tan A - \sec A + 1}}\]

On canceling common term, we get

\[ \Rightarrow \sec A + \tan A\]

Now, we will convert above written expression in terms of $\sin e$ and $\cos $.

\[ \Rightarrow \dfrac{1}{{\cos A}} + \dfrac{{\sin A}}{{\cos A}}\]

Take LCM

\[ \Rightarrow \dfrac{{1 + \sin A}}{{\cos A}}\]

Hence proved.

2. If $\dfrac{{2\sin \alpha }}{{1 + \cos \alpha  + \sin \alpha }} = y$, prove that $\dfrac{{1 - \cos \alpha  + \sin \alpha }}{{1 + \sin \alpha }}$ is also equal to $y$.

Ans: Given, $y = \dfrac{{2\sin \alpha }}{{1 + \cos \alpha  + \sin \alpha }}$

Let us multiply and divide the above written expression by $1 + \sin \alpha  - \cos \alpha $.

$ \Rightarrow \dfrac{{2\sin \alpha }}{{1 + \cos \alpha  + \sin \alpha }} \times \dfrac{{1 + \sin \alpha  - \cos \alpha }}{{1 + \sin \alpha  - \cos \alpha }}$

$ \Rightarrow \dfrac{{2\sin \alpha \left( {1 + \sin \alpha  - \cos \alpha } \right)}}{{\left( {1 + \cos \alpha  + \sin \alpha } \right)\left( {1 + \sin \alpha  - \cos \alpha } \right)}}$

Now we will apply $\left( {a + b} \right)\left( {a - b} \right) = {a^2} - {b^2}$ formula to simplify the denominator.

$ \Rightarrow \dfrac{{2\sin \alpha \left( {1 + \sin \alpha  - \cos \alpha } \right)}}{{{{\left( {1 + \sin \alpha } \right)}^2} - {{\cos }^2}\alpha }}$

On expansion using ${\left( {a + b} \right)^2} = {a^2} + {b^2} + 2ab$ , we get

$ \Rightarrow \dfrac{{2\sin \alpha \left( {1 + \sin \alpha  - \cos \alpha } \right)}}{{{1^2} + {{\sin }^2}\alpha  + 2\sin \alpha  - {{\cos }^2}\alpha }}$

$ \Rightarrow \dfrac{{2\sin \alpha \left( {1 + \sin \alpha  - \cos \alpha } \right)}}{{\left( {{1^2} - {{\cos }^2}\alpha } \right) + {{\sin }^2}\alpha  + 2\sin \alpha }}$

We know that \[1 - {\cos ^2}x = {\sin ^2}x\]. Therefore, we get

$ \Rightarrow \dfrac{{2\sin \alpha \left( {1 + \sin \alpha  - \cos \alpha } \right)}}{{{{\sin }^2}\alpha  + {{\sin }^2}\alpha  + 2\sin \alpha }}$

$ \Rightarrow \dfrac{{2\sin \alpha \left( {1 + \sin \alpha  - \cos \alpha } \right)}}{{2{{\sin }^2}\alpha  + 2\sin \alpha }}$

Take $2\sin \alpha $ as a common term

$ \Rightarrow \dfrac{{2\sin \alpha \left( {1 + \sin \alpha  - \cos \alpha } \right)}}{{2\sin \alpha \left( {\sin \alpha  + 1} \right)}}$

On canceling common term, we get

$ \Rightarrow \dfrac{{1 + \sin \alpha  - \cos \alpha }}{{\sin \alpha  + 1}} = y$

Hence proved.

3. If $m\sin \theta  = n\sin \left( {\theta  + 2\alpha } \right)$, then prove that $\tan \left( {\theta  + \alpha } \right)\cot \alpha  = \dfrac{{m + n}}{{m - n}}$.

Ans: Given, $m\sin \theta  = n\sin \left( {\theta  + 2\alpha } \right)$

We can also write it as,

$ \Rightarrow \dfrac{{\sin \left( {\theta  + 2\alpha } \right)}}{{\sin \theta }} = \dfrac{m}{n}$

Now, we will apply componendo and dividend rule on the above written expression.

$ \Rightarrow \dfrac{{\sin \left( {\theta  + 2\alpha } \right) + \sin \theta }}{{\sin \left( {\theta  + 2\alpha } \right) - \sin \theta }} = \dfrac{{m + n}}{{m - n}}$

We know that $\sin A + \sin B = 2\sin \dfrac{{A + B}}{2}.\cos \dfrac{{A - B}}{2}$ and $\sin A - \sin B = 2\cos \dfrac{{A + B}}{2}.\sin \dfrac{{A - B}}{2}$. Therefore, we get

$ \Rightarrow \dfrac{{2\sin \left( {\dfrac{{\theta  + 2\alpha  + \theta }}{2}} \right).\cos \left( {\dfrac{{\theta  + 2\alpha  - \theta }}{2}} \right)}}{{2\cos \left( {\dfrac{{\theta  + 2\alpha  + \theta }}{2}} \right).\sin \left( {\dfrac{{\theta  + 2\alpha  - \theta }}{2}} \right)}} = \dfrac{{m + n}}{{m - n}}$

$ \Rightarrow \dfrac{{2\sin \left( {\dfrac{{2\theta  + 2\alpha }}{2}} \right).\cos \left( {\dfrac{{2\alpha }}{2}} \right)}}{{2\cos \left( {\dfrac{{2\theta  + 2\alpha }}{2}} \right).\sin \left( {\dfrac{{2\alpha }}{2}} \right)}} = \dfrac{{m + n}}{{m - n}}$

On simplification, we get

$ \Rightarrow \dfrac{{2\sin \left( {\theta  + \alpha } \right).\cos \left( \alpha  \right)}}{{2\cos \left( {\theta  + \alpha } \right).\sin \left( \alpha  \right)}} = \dfrac{{m + n}}{{m - n}}$

Now we will write above written expression in terms of $\tan $ and $\cot $.

$ \Rightarrow \tan \left( {\theta  + \alpha } \right).\cot \alpha  = \dfrac{{m + n}}{{m - n}}$

Hence proved.

4. If $\cos \left( {\alpha  + \beta } \right) = \dfrac{4}{5}$ and $\sin \left( {\alpha  - \beta } \right) = \dfrac{5}{{13}}$, where $\alpha $ lie between $0$ and $\dfrac{\pi }{4}$, find the value of $\tan 2\alpha $.

Ans: Given, $\cos \left( {\alpha  + \beta } \right) = \dfrac{4}{5}$ and $\sin \left( {\alpha  - \beta } \right) = \dfrac{5}{{13}}$

At first we will find the value $\tan \left( {\alpha  + \beta } \right)$ and $\tan \left( {\alpha  - \beta } \right)$.

For value of $\tan \left( {\alpha  + \beta } \right)$, we have

$ \Rightarrow \cos \left( {\alpha  + \beta } \right) = \dfrac{4}{5} = \dfrac{B}{H}$

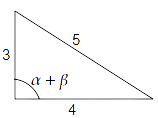
We know that ${H^2} = {P^2} + {B^2}$ 

$ \Rightarrow {5^2} = {P^2} + {4^2}$

$ \Rightarrow {P^2} = {5^2} - {4^2} = 25 - 16$

$ \Rightarrow {P^2} = 9$

$ \Rightarrow P = 3$

We know that $\tan x = \dfrac{P}{B}$. Therefore, we get

$ \Rightarrow \tan \left( {\alpha  + \beta } \right) = \dfrac{3}{4}$

For value of $\tan \left( {\alpha  - \beta } \right)$, we have

$ \Rightarrow \sin \left( {\alpha  - \beta } \right) = \dfrac{5}{{13}} = \dfrac{P}{H}$

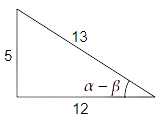
We know that ${H^2} = {P^2} + {B^2}$ 

$ \Rightarrow {13^2} = {5^2} + {B^2}$

$ \Rightarrow {B^2} = {13^2} - {5^2} = 169 - 25$

$ \Rightarrow {B^2} = 144$

$ \Rightarrow B = 12$

We know that $\tan x = \dfrac{P}{B}$. Therefore, we get

$ \Rightarrow \tan \left( {\alpha  - \beta } \right) = \dfrac{5}{{12}}$

As here we need to find value of $\tan 2\alpha $, we can write it as

$ \Rightarrow \tan 2\alpha  = \left[ {\alpha  + \beta  + \alpha  - \beta } \right]$

$ \Rightarrow \tan 2\alpha  = \left[ {\left( {\alpha  + \beta } \right) + \left( {\alpha  - \beta } \right)} \right]$

We know that $\tan \left( {x + y} \right) = \dfrac{{\tan x + \tan y}}{{1 - \tan x\tan y}}$. Therefore, we get

$ \Rightarrow \tan 2\alpha  = \dfrac{{\tan \left( {\alpha  + \beta } \right) + \tan \left( {\alpha  - \beta } \right)}}{{1 - \tan \left( {\alpha  + \beta } \right)\tan \left( {\alpha  - \beta } \right)}}$

$ \Rightarrow \tan 2\alpha  = \dfrac{{\dfrac{3}{4} + \dfrac{5}{{12}}}}{{1 - \dfrac{3}{4} \times \dfrac{5}{{12}}}}$

$ \Rightarrow \tan 2\alpha  = \dfrac{{\dfrac{{9 + 5}}{{12}}}}{{\dfrac{{48 - 15}}{{48}}}}$

$ \Rightarrow \tan 2\alpha  = \dfrac{{14}}{{12}} \times \dfrac{{48}}{{33}}$

$ \Rightarrow \tan 2\alpha  = \dfrac{{56}}{{33}}$

This is our required answer.

5. If $\tan x = \dfrac{b}{a}$, then find the value of $\sqrt {\dfrac{{a + b}}{{a - b}}}  + \sqrt {\dfrac{{a - b}}{{a + b}}} $.

Ans: Given, $\tan x = \dfrac{b}{a}$ and we need to find the value of $\sqrt {\dfrac{{a + b}}{{a - b}}}  + \sqrt {\dfrac{{a - b}}{{a + b}}} $.

Let us first take LCM of the above written expression

\[ \Rightarrow \dfrac{{\sqrt {a + b}  \times \sqrt {a + b}  + \sqrt {a - b}  \times \sqrt {a - b} }}{{\sqrt {a - b}  \times \sqrt {a + b} }}\]

On multiplication of terms, we get

\[ \Rightarrow \dfrac{{{{\left( {\sqrt {a + b} } \right)}^2} + {{\left( {\sqrt {a - b} } \right)}^2}}}{{\sqrt {\left( {a - b} \right)\left( {a + b} \right)} }}\]

As we know $\left( {a - b} \right)\left( {a + b} \right) = {a^2} + {b^2}$. Therefore, we get

\[ \Rightarrow \dfrac{{a + b + a - b}}{{\sqrt {{a^2} - {b^2}} }}\]

\[ \Rightarrow \dfrac{{2a}}{{a\sqrt {1 - \dfrac{{{b^2}}}{{{a^2}}}} }}\]

We are given that $\tan x = \dfrac{b}{a}$. Therefore, we get

\[ \Rightarrow \dfrac{2}{{\sqrt {1 - {{\tan }^2}x} }}\]

We can also write it as,

\[ \Rightarrow \dfrac{2}{{\sqrt {1 - \dfrac{{{{\sin }^2}x}}{{{{\cos }^2}x}}} }}\]

On taking LCM, we get

\[ \Rightarrow \dfrac{2}{{\sqrt {\dfrac{{{{\cos }^2}x - {{\sin }^2}x}}{{{{\cos }^2}x}}} }}\]

We know that \[{\cos ^2}x - {\sin ^2}x = \cos 2x\]. Therefore, we get

\[ \Rightarrow \dfrac{2}{{\dfrac{{\sqrt {\cos 2x} }}{{\cos x}}}}\]

\[ \Rightarrow \dfrac{{2\cos x}}{{\sqrt {\cos 2x} }}\]

Hence, $\sqrt {\dfrac{{a + b}}{{a - b}}}  + \sqrt {\dfrac{{a - b}}{{a + b}}}  = \dfrac{{2\cos x}}{{\sqrt {\cos 2x} }}$.

6. Prove that $\cos \theta \cos \dfrac{\theta }{2} - \cos 3\theta \cos \dfrac{{9\theta }}{2} = \sin 4\theta \sin \left( {\dfrac{{7\theta }}{2}} \right)$.

Ans: We need to prove that $\cos \theta \cos \dfrac{\theta }{2} - \cos 3\theta \cos \dfrac{{9\theta }}{2} = \sin 4\theta \sin \left( {\dfrac{{7\theta }}{2}} \right)$

Let us start to solve L.H.S. = $\cos \theta \cos \dfrac{\theta }{2} - \cos 3\theta \cos \dfrac{{9\theta }}{2}$

On multiplication and division of the above written expression by $2$, we get

$ \Rightarrow \dfrac{1}{2}\left[ {2\cos \theta \cos \dfrac{\theta }{2}} \right] - \dfrac{1}{2}\left[ {2\cos 3\theta \cos \dfrac{{9\theta }}{2}} \right]$

Now, we will apply $\cos \left( {A + B} \right) + \cos \left( {A - B} \right) = 2\cos A\cos B$ formula.

$ \Rightarrow \dfrac{1}{2}\left[ {\cos \left( {\theta  + \dfrac{\theta }{2}} \right) + \cos \left( {\theta  - \dfrac{\theta }{2}} \right)} \right] - \dfrac{1}{2}\left[ {\cos \left( {3\theta  + \dfrac{{9\theta }}{2}} \right) + \cos \left( {3\theta  - \dfrac{{9\theta }}{2}} \right)} \right]$

On simplification, we get

$ \Rightarrow \dfrac{1}{2}\left[ {\cos \dfrac{{3\theta }}{2} + \cos \dfrac{\theta }{2}} \right] - \dfrac{1}{2}\left[ {\cos \dfrac{{15\theta }}{2} + \cos \left( { - \dfrac{{3\theta }}{2}} \right)} \right]$

$ \Rightarrow \dfrac{1}{2}\left[ {\cos \dfrac{{3\theta }}{2} + \cos \dfrac{\theta }{2} - \cos \dfrac{{15\theta }}{2} - \cos \left( { - \dfrac{{3\theta }}{2}} \right)} \right]$

As we know $\cos \left( { - \theta } \right) = \cos \theta $. Therefore, we get

$ \Rightarrow \dfrac{1}{2}\left[ {\cos \dfrac{{3\theta }}{2} + \cos \dfrac{\theta }{2} - \cos \dfrac{{15\theta }}{2} - \cos \dfrac{{3\theta }}{2}} \right]$

$ \Rightarrow \dfrac{1}{2}\left[ {\cos \dfrac{\theta }{2} - \cos \dfrac{{15\theta }}{2}} \right]$

We know that $\cos C - \cos D =  - 2\sin \left( {\dfrac{{C + D}}{2}} \right)\sin \left( {\dfrac{{C - D}}{2}} \right)$. Therefore, we get

\[ \Rightarrow \dfrac{1}{2}\left[ { - 2\sin \left( {\dfrac{{\dfrac{\theta }{2} + \dfrac{{15\theta }}{2}}}{2}} \right)\sin \left( {\dfrac{{\dfrac{\theta }{2} - \dfrac{{15\theta }}{2}}}{2}} \right)} \right]\]

\[ \Rightarrow  - \sin \left( {\dfrac{{\dfrac{{16\theta }}{2}}}{2}} \right)\sin \left( {\dfrac{{\dfrac{{ - 14\theta }}{2}}}{2}} \right)\]

\[ \Rightarrow  - \sin \left( {4\theta } \right)\sin \left( {\dfrac{{ - 7\theta }}{2}} \right)\]

As we know $\sin \left( { - \theta } \right) =  - \sin \theta $. Therefore, we get

\[ \Rightarrow \sin \left( {4\theta } \right)\sin \left( {\dfrac{{7\theta }}{2}} \right)\]

Hence proved.

7. If $a\cos \theta  + b\sin \theta  = m$ and $a\sin \theta  - b\cos \theta  = n$, then show that ${a^2} + {b^2} = {m^2} + {n^2}$.

Ans: Given, $a\cos \theta  + b\sin \theta  = m$ and $a\sin \theta  - b\cos \theta  = n$

$ \Rightarrow a\cos \theta  + b\sin \theta  = m$

On squaring both the side, we get

$ \Rightarrow {\left( {a\cos \theta  + b\sin \theta } \right)^2} = {m^2}$

$ \Rightarrow {a^2}{\cos ^2}\theta  + {b^2}{\sin ^2}\theta  + 2ab\sin \theta \cos \theta  = {m^2}.....\left( i \right)$

$ \Rightarrow a\sin \theta  - b\cos \theta  = n$

On squaring both the side, we get

$ \Rightarrow {\left( {a\sin \theta  - b\cos \theta } \right)^2} = {n^2}$

$ \Rightarrow {a^2}{\sin ^2}\theta  + {b^2}{\cos ^2}\theta  - 2ab\sin \theta \cos \theta  = {n^2}.....\left( {ii} \right)$

Add equation $\left( i \right)$ and $\left( {ii} \right)$.

$ \Rightarrow {m^2} + {n^2} = {a^2}{\cos ^2}\theta  + {b^2}{\sin ^2}\theta  + 2ab\sin \theta \cos \theta  + {a^2}{\sin ^2}\theta  + {b^2}{\cos ^2}\theta  - 2ab\sin \theta \cos \theta $

$ \Rightarrow {m^2} + {n^2} = {a^2}\left( {{{\cos }^2}\theta  + {{\sin }^2}\theta } \right) + {b^2}\left( {{{\sin }^2}\theta  + {{\cos }^2}\theta } \right)$

As we know ${\sin ^2}\theta  + {\cos ^2}\theta  = 1$. Therefore, we get

$ \Rightarrow {m^2} + {n^2} = {a^2}\left( 1 \right) + {b^2}\left( 1 \right)$

$ \Rightarrow {m^2} + {n^2} = {a^2} + {b^2}$

Hence proved.

8. Find the value of $\tan 20^\circ 30'$.

Ans: We need to find the value of $\tan 20^\circ 30'$.

Let $22^\circ 33' = \dfrac{\theta }{2}$ 

$ \Rightarrow \theta  = 45^\circ $ 

$ \Rightarrow \tan 20^\circ 30' = \tan \dfrac{\theta }{2}$

We know that $\tan x = \dfrac{{\sin x}}{{\cos x}}$. Therefore, we get

$ \Rightarrow \tan 20^\circ 30' = \dfrac{{\sin \dfrac{\theta }{2}}}{{\cos \dfrac{\theta }{2}}}$

Multiply numerator and denominator by $2\cos \dfrac{\theta }{2}$ 

$ \Rightarrow \tan 20^\circ 30' = \dfrac{{2\sin \dfrac{\theta }{2}\cos \dfrac{\theta }{2}}}{{2\cos \dfrac{\theta }{2}\cos \dfrac{\theta }{2}}}$

$ \Rightarrow \tan 20^\circ 30' = \dfrac{{2\sin \dfrac{\theta }{2}\cos \dfrac{\theta }{2}}}{{2{{\cos }^2}\dfrac{\theta }{2}}}$

We know that $\sin x = 2\sin \dfrac{x}{2}\cos \dfrac{x}{2}$ and $2{\cos ^2}\dfrac{x}{2} = 1 + \cos x$. Therefore, we get

$ \Rightarrow \tan 20^\circ 30' = \dfrac{{\sin \theta }}{{1 + \cos \theta }}$

Put $\theta  = 45^\circ $ 

$ \Rightarrow \tan 20^\circ 30' = \dfrac{{\sin 45^\circ }}{{1 + \cos 45^\circ }}$

Substitute value of $\sin 45^\circ  = \dfrac{1}{{\sqrt 2 }}$ and $\cos 45^\circ  = \dfrac{1}{{\sqrt 2 }}$

$ \Rightarrow \tan 20^\circ 30' = \dfrac{{\dfrac{1}{{\sqrt 2 }}}}{{1 + \dfrac{1}{{\sqrt 2 }}}}$

$ \Rightarrow \tan 20^\circ 30' = \dfrac{{\dfrac{1}{{\sqrt 2 }}}}{{\dfrac{{\sqrt 2  + 1}}{{\sqrt 2 }}}}$

$ \Rightarrow \tan 20^\circ 30' = \dfrac{1}{{\sqrt 2  + 1}}$

Multiply numerator and denominator by $\sqrt 2  - 1$ 

$ \Rightarrow \tan 20^\circ 30' = \dfrac{1}{{\sqrt 2  + 1}} \times \dfrac{{\sqrt 2  - 1}}{{\sqrt 2  - 1}}$

$ \Rightarrow \tan 20^\circ 30' = \dfrac{{\sqrt 2  - 1}}{{2 - 1}}$

$ \Rightarrow \tan 20^\circ 30' = \sqrt 2  - 1$

This is our required answer.

9. Prove that $\sin 4A = 4\sin A{\cos ^3}A - 4\cos A{\sin ^3}A$.

Ans: We need to prove that $\sin 4A = 4\sin A{\cos ^3}A - 4\cos A{\sin ^3}A$

We can write $\sin 4A = \sin \left( {A + 3A} \right)$

As we know $\sin \left( {A + B} \right) = \sin A\cos B.\cos A\sin B$. Therefore, we get

$ \Rightarrow \sin 4A = \sin A\cos 3A + \cos A\sin 3A$

As we know $\cos 3A = 4{\cos ^3}A - 3\cos A$ and $\sin 3A = 3\sin A - 4{\sin ^3}A$. Therefore, we get

$ \Rightarrow \sin 4A = \sin A\left( {4{{\cos }^3}A - 3\cos A} \right) + \cos A\left( {3\sin A - 4{{\sin }^3}A} \right)$

On multiplication of terms, we get

$ \Rightarrow \sin 4A = 4\sin A{\cos ^3}A - 3\sin A\cos A + 3\cos A\sin A - 4\cos A{\sin ^3}A$

$ \Rightarrow \sin 4A = 4\sin A{\cos ^3}A - 4\cos A{\sin ^3}A$

Hence proved.

10.  If $\tan \theta  + \sin \theta  = m$ and $\tan \theta  - \sin \theta  = n$, then prove that ${m^2} - {n^2} = 4\sin \theta \tan \theta $.

Ans: Given, $\tan \theta  + \sin \theta  = m$ and $\tan \theta  - \sin \theta  = n$

$ \Rightarrow \tan \theta  + \sin \theta  = m$

On squaring both the sides, we get

$ \Rightarrow {\left( {\tan \theta  + \sin \theta } \right)^2} = {m^2}$

As we know ${\left( {a + b} \right)^2} = {a^2} + {b^2} + 2ab$. Therefore, we get

$ \Rightarrow {\tan ^2}\theta  + {\sin ^2}\theta  + 2\tan \theta \sin \theta  = {m^2}....\left( i \right)$

$ \Rightarrow \tan \theta  - \sin \theta  = n$

On squaring both the sides, we get

$ \Rightarrow {\left( {\tan \theta  - \sin \theta } \right)^2} = {n^2}$

As we know ${\left( {a + b} \right)^2} = {a^2} + {b^2} + 2ab$. Therefore, we get

$ \Rightarrow {\tan ^2}\theta  + {\sin ^2}\theta  - 2\tan \theta \sin \theta  = {n^2}....\left( {ii} \right)$

Now, we will subtract equation $\left( {ii} \right)$ from $\left( i \right)$.

$ \Rightarrow {m^2} - {n^2} = {\tan ^2}\theta  + {\sin ^2}\theta  + 2\tan \theta \sin \theta  - \left( {{{\tan }^2}\theta  + {{\sin }^2}\theta  - 2\tan \theta \sin \theta } \right)$

$ \Rightarrow {m^2} - {n^2} = {\tan ^2}\theta  + {\sin ^2}\theta  + 2\tan \theta \sin \theta  - {\tan ^2}\theta  - {\sin ^2}\theta  + 2\tan \theta \sin \theta $

On subtraction of terms, we get

$ \Rightarrow {m^2} - {n^2} = 2\tan \theta \sin \theta  + 2\tan \theta \sin \theta $

$ \Rightarrow {m^2} - {n^2} = 4\sin \theta \tan \theta $

Hence proved.

11.  If $\tan \left( {A + B} \right) = p$, $\tan \left( {A - B} \right) = q$, then show that $\tan 2A = \dfrac{{p + q}}{{1 - pq}}$.

Ans: Given, $\tan \left( {A + B} \right) = p$ and $\tan \left( {A - B} \right) = q$

Let us start with LHS of $\tan 2A = \dfrac{{p + q}}{{1 - pq}}$.

$ \Rightarrow \tan 2A = \tan \left( {A + B + A - B} \right)$

This can also be written as,

$ \Rightarrow \tan 2A = \tan \left[ {\left( {A + B} \right) + \left( {A - B} \right)} \right]$

We know that $\tan \left( {x + y} \right) = \dfrac{{\tan x + \tan y}}{{1 - \tan x\tan y}}$. Now, we will apply this formula on the RHS.

$ \Rightarrow \tan 2A = \dfrac{{\tan \left( {A + B} \right) + \tan \left( {A - B} \right)}}{{1 - \tan \left( {A + B} \right)\tan \left( {A - B} \right)}}$

We are given that $\tan \left( {A + B} \right) = p$ and $\tan \left( {A - B} \right) = q$. Therefore, we get

$ \Rightarrow \tan 2A = \dfrac{{p + q}}{{1 - pq}}$

Hence proved.

12.  If $\cos \alpha  + \cos \beta  = 0 = \sin \alpha  + \sin \beta $, then prove that $\cos 2\alpha  + \cos 2\beta  =  - 2\cos \left( {\alpha  + \beta } \right)$.

Ans: Given, $\cos \alpha  + \cos \beta  = 0$ and $\sin \alpha  + \sin \beta  = 0$.

$ \Rightarrow {\left( {\cos \alpha  + \cos \beta } \right)^2} = 0$

On squaring both the sides, we get

$ \Rightarrow {\cos ^2}\alpha  + {\cos ^2}\beta  + 2\cos \alpha \cos \beta  = 0........\left( 1 \right)$

$ \Rightarrow \sin \alpha  + \sin \beta  = 0$

On squaring both the sides, we get

$ \Rightarrow {\left( {\sin \alpha  + \sin \beta } \right)^2} = 0$

$ \Rightarrow {\sin ^2}\alpha  + {\sin ^2}\beta  + 2\sin \alpha \sin \beta  = 0.......\left( 2 \right)$

Now, we will subtract equation $\left( 2 \right)$ from $\left( 1 \right)$.$ \Rightarrow {\cos ^2}\alpha  + {\cos ^2}\beta  + 2\cos \alpha \cos \beta  - \left( {{{\sin }^2}\alpha  + {{\sin }^2}\beta  + 2\sin \alpha \sin \beta } \right) = 0$

$ \Rightarrow {\cos ^2}\alpha  + {\cos ^2}\beta  + 2\cos \alpha \cos \beta  - {\sin ^2}\alpha  - {\sin ^2}\beta  - 2\sin \alpha \sin \beta  = 0$

$ \Rightarrow {\cos ^2}\alpha  - {\sin ^2}\alpha  + {\cos ^2}\beta  - {\sin ^2}\beta  + 2\cos \alpha \cos \beta  - 2\sin \alpha \sin \beta  = 0$

We know that ${\cos ^2}x - {\sin ^2}x = \cos 2x$. Therefore, we get

\[ \Rightarrow \cos 2\alpha  + \cos 2\beta  + 2\left( {\cos \alpha \cos \beta  - \sin \alpha \sin \beta } \right) = 0\]

We know that $\cos \left( {A + B} \right) = \cos A\cos B - \sin A\sin B$. Therefore, we get

\[ \Rightarrow \cos 2\alpha  + \cos 2\beta  + 2\cos \left( {\alpha  + \beta } \right) = 0\]

\[ \Rightarrow \cos 2\alpha  + \cos 2\beta  =  - 2\cos \left( {\alpha  + \beta } \right)\]

Hence proved.

13.  If $\dfrac{{\sin \left( {x + y} \right)}}{{\sin \left( {x - y} \right)}} = \dfrac{{a + b}}{{a - b}}$, then show that $\dfrac{{\tan x}}{{\tan y}} = \dfrac{a}{b}$.

Ans: Given, $\dfrac{{\sin \left( {x + y} \right)}}{{\sin \left( {x - y} \right)}} = \dfrac{{a + b}}{{a - b}}$

We will apply componendo and dividend rule on the above written expression.

$ \Rightarrow \dfrac{{\sin \left( {x + y} \right) + \sin \left( {x - y} \right)}}{{\sin \left( {x + y} \right) - \sin \left( {x - y} \right)}} = \dfrac{{a + b + a + b}}{{a + b - \left( {a - b} \right)}}$

We know that $\sin A + \sin B = 2\sin \dfrac{{A + B}}{2}.\cos \dfrac{{A - B}}{2}$ and $\sin A - \sin B = 2\cos \dfrac{{A + B}}{2}.\sin \dfrac{{A - B}}{2}$. Therefore, we get

$ \Rightarrow \dfrac{{2\sin \left( {\dfrac{{x + y + x - y}}{2}} \right)\cos \left( {\dfrac{{x + y - x + y}}{2}} \right)}}{{2\cos \left( {\dfrac{{x + y + x - y}}{2}} \right)\sin \left( {\dfrac{{x + y - x + y}}{2}} \right)}} = \dfrac{{a + b + a + b}}{{a + b - a + b}}$

On simplification, we get

$ \Rightarrow \dfrac{{2\sin \left( {\dfrac{{2x}}{2}} \right)\cos \left( {\dfrac{{2y}}{2}} \right)}}{{2\cos \left( {\dfrac{{2x}}{2}} \right)\sin \left( {\dfrac{{2y}}{2}} \right)}} = \dfrac{{2\left( {a + b} \right)}}{{2b}}$

On canceling common terms, we get

$ \Rightarrow \dfrac{{\sin x\cos y}}{{\cos x\sin y}} = \dfrac{{a + b}}{b}$

Now we will write above written expression in terms of $\tan $ and $\cot $.

$ \Rightarrow \tan x.\cot y = \dfrac{{a + b}}{b}$

\[ \Rightarrow \dfrac{{\tan x}}{{\tan y}} = \dfrac{{a + b}}{b}\]

Hence proved.

14.  If $\tan \theta  = \dfrac{{\sin \alpha  - \cos \alpha }}{{\sin \alpha  + \cos \alpha }}$, then show that $\sin \alpha  + \cos \alpha  = \sqrt 2 \cos \theta $.

Ans: Given, $\tan \theta  = \dfrac{{\sin \alpha  - \cos \alpha }}{{\sin \alpha  + \cos \alpha }}$

Divide numerator and denominator of RHS by $\cos \alpha $.

$ \Rightarrow \tan \theta  = \dfrac{{\dfrac{{\sin \alpha  - \cos \alpha }}{{\cos \alpha }}}}{{\dfrac{{\sin \alpha  + \cos \alpha }}{{\cos \alpha }}}}$

$ \Rightarrow \tan \theta  = \dfrac{{\dfrac{{\sin \alpha }}{{\cos \alpha }} - \dfrac{{\cos \alpha }}{{\cos \alpha }}}}{{\dfrac{{\sin \alpha }}{{\cos \alpha }} + \dfrac{{\cos \alpha }}{{\cos \alpha }}}}$

As we know $\dfrac{{\sin x}}{{\cos x}} = \tan x$. Therefore, we get

$ \Rightarrow \tan \theta  = \dfrac{{\tan \alpha  - 1}}{{\tan \alpha  + 1}}$

We know that $\tan \dfrac{\pi }{4} = 1$. So, we can write above written equation as,

$ \Rightarrow \tan \theta  = \dfrac{{\tan \alpha  - \tan \dfrac{\pi }{4}}}{{\tan \alpha  + \tan \dfrac{\pi }{4}}}$

We know that $\tan \left( {x - y} \right) = \dfrac{{\tan x - \tan y}}{{1 + \tan x\tan y}}$. Therefore, we get

$ \Rightarrow \tan \theta  = \tan \left( {\alpha  - \dfrac{\pi }{4}} \right)$

$\therefore \theta  = \alpha  - \dfrac{\pi }{4}$

$ \Rightarrow \cos \theta  = \cos \left( {\alpha  - \dfrac{\pi }{4}} \right)$

We know that $\cos \left( {A - B} \right) = \cos A.\cos B + \sin A.\sin B$. Therefore, we get

$ \Rightarrow \cos \theta  = \cos \alpha .\cos \dfrac{\pi }{4} + \sin \alpha .\sin \dfrac{\pi }{4}$

Substitute values of $\cos \dfrac{\pi }{4} = \dfrac{1}{{\sqrt 2 }}$ and $\sin \dfrac{\pi }{4} = \dfrac{1}{{\sqrt 2 }}$

$ \Rightarrow \cos \theta  = \cos \alpha .\dfrac{1}{{\sqrt 2 }} + \sin \alpha .\dfrac{1}{{\sqrt 2 }}$

Multiply both sides by $\sqrt 2 $.

\[ \Rightarrow \sqrt 2 \cos \theta  = \cos \alpha  + \sin \alpha \]

\[ \Rightarrow \sin \alpha  + \cos \alpha  = \sqrt 2 \cos \theta \]

Hence proved.

15.  If $\sin \theta  + \cos \theta  = 1$, then find the general value of $\theta $.

Ans: We have, $\sin \theta  + \cos \theta  = 1$

Divide both sides by $\sqrt 2 $.

$ \Rightarrow \dfrac{1}{{\sqrt 2 }}\sin \theta  + \dfrac{1}{{\sqrt 2 }}\cos \theta  = \dfrac{1}{{\sqrt 2 }}$ 

We know that $\dfrac{1}{{\sqrt 2 }} = \sin \dfrac{\pi }{4}$ and $\dfrac{1}{{\sqrt 2 }} = \cos \dfrac{\pi }{4}$. Therefore, we get

$ \Rightarrow \sin \dfrac{\pi }{4}\sin \theta  + \cos \dfrac{\pi }{4}\cos \theta  = \dfrac{1}{{\sqrt 2 }}$

We know that $\cos \left( {A - B} \right) = \cos A\cos B + \sin A\sin B$. So, we can write above-written expression as

$ \Rightarrow \cos \left( {\theta  - \dfrac{\pi }{4}} \right) = \cos \dfrac{\pi }{4}$

We know that if $\cos \theta  = \cos \alpha $, then $\theta  = 2n\pi  \pm \alpha $. Therefore, we get

$ \Rightarrow \theta  - \dfrac{\pi }{4} = 2n\pi  \pm \dfrac{\pi }{4},n \in Z$

Transport $ - \dfrac{\pi }{4}$ to RHS

$ \Rightarrow \theta  = 2n\pi  \pm \dfrac{\pi }{4} - \dfrac{\pi }{4}$

$ \Rightarrow \theta  = 2n\pi  + \dfrac{\pi }{4} + \dfrac{\pi }{4}$ or $ \Rightarrow \theta  = 2n\pi  - \dfrac{\pi }{4} + \dfrac{\pi }{4}$

$ \Rightarrow \theta  = 2n\pi  + \dfrac{\pi }{2}$ or $ \Rightarrow \theta  = 2n\pi ,n \in Z$

Therefore, the general values of $\theta $ are $2n\pi  + \dfrac{\pi }{2}$ and $2n\pi $ where $n \in Z$.

16.  Find the most general value of $\theta $ satisfying the equation $\tan \theta  =  - 1$ and $\cos \theta  = \dfrac{1}{{\sqrt 2 }}$.

Ans: We have, $\tan \theta  =  - 1$ and $\cos \theta  = \dfrac{1}{{\sqrt 2 }}$.

As we can see $\tan \theta $ is negative and $\cos \theta $. It means $\theta $ lies in the fourth quadrant.

We have, $\tan \theta  =  - 1$

$ \Rightarrow \tan \theta  = \tan \left( { - \dfrac{\pi }{4}} \right)$

$ \Rightarrow \tan \theta  = \tan \left( { - \dfrac{\pi }{4}} \right)$

We know that $\tan \left( {2\pi  - x} \right) =  - \tan x$. So, we can write above written expression as

$ \Rightarrow \tan \theta  = \tan \left( {2\pi  - \dfrac{\pi }{4}} \right)$

$ \Rightarrow \tan \theta  = \tan \left( {\dfrac{{7\pi }}{4}} \right)$

$ \Rightarrow \theta  = \dfrac{{7\pi }}{4}$

We have, $\cos \theta  = \dfrac{1}{{\sqrt 2 }}$

$ \Rightarrow \cos \theta  = \cos \dfrac{\pi }{4}$

We know that $\cos \left( {2\pi  - x} \right) = \cos x$. So, we can write above written expression as

$ \Rightarrow \cos \theta  = \cos \left( {2\pi  - \dfrac{\pi }{4}} \right)$

$ \Leftarrow \cos \theta  = \cos \dfrac{{7\pi }}{4}$

$ \Rightarrow \theta  = \dfrac{{7\pi }}{4}$

Therefore, the general solution is $\theta  = 2n\pi  + \dfrac{{7\pi }}{4},n \in Z$.

17.  If $\cot \theta  + \tan \theta  = 2\cos ec\theta $, then find the general value of $\theta $.

Ans: Given, $\cot \theta  + \tan \theta  = 2\cos ec\theta $

Let us write above written expression in terms of $\sin $ and $\cos $.

\[ \Rightarrow \dfrac{{\cos \theta }}{{\sin \theta }} + \dfrac{{\sin \theta }}{{\cos \theta }} = \dfrac{2}{{\sin \theta }}\]

Take LCM

\[ \Rightarrow \dfrac{{{{\cos }^2}\theta  + {{\sin }^2}\theta }}{{\sin \theta \cos \theta }} = \dfrac{2}{{\sin \theta }}\]

We know that ${\sin ^2}\theta  + {\cos ^2}\theta  = 1$. Therefore, we get

\[ \Rightarrow \dfrac{1}{{\sin \theta \cos \theta }} = \dfrac{2}{{\sin \theta }}\]

On cross multiplication, we get

\[ \Rightarrow \dfrac{1}{{\sin \theta \cos \theta }} = \dfrac{2}{{\sin \theta }}\]

\[ \Rightarrow 2\sin \theta \cos \theta  = \sin \theta \]

Transport $\sin \theta $ to LHS

\[ \Rightarrow 2\sin \theta \cos \theta  - \sin \theta  = 0\]

\[ \Rightarrow \sin \theta \left( {2\cos \theta  - 1} \right) = 0\]

\[ \Rightarrow \sin \theta  = 0\] or \[2\cos \theta  - 1 = 0\]

\[ \Rightarrow \sin \theta  = 0\] or \[\cos \theta  = \dfrac{1}{2}\]

As we have, \[\sin \theta  = 0\]

$ \Rightarrow \theta  = n\pi ,n \in Z$ 

As we have, \[\cos \theta  = \dfrac{1}{2}\]

$ \Rightarrow \cos \theta  = \cos \dfrac{\pi }{3}$ 

$ \Rightarrow \theta  = 2n\pi  \pm \dfrac{\pi }{3}$ 

Therefore, the general value of $\theta $ is $2n\pi  \pm \dfrac{\pi }{3}$ and $n\pi $, $n \in Z$.

18.  If $2{\sin ^2}\theta  = 3\cos \theta $, where $0 \leqslant \theta  \leqslant 2\pi $, then find the value of $\theta $.

Ans: Given, $2{\sin ^2}\theta  = 3\cos \theta $

We know that ${\sin ^2}x = 1 - {\cos ^2}x$. Therefore, we get

$ \Rightarrow 2\left( {1 - {{\cos }^2}\theta } \right) = 3\cos \theta $

$ \Rightarrow 2 - 2{\cos ^2}\theta  = 3\cos \theta $

$ \Rightarrow 2{\cos ^2}\theta  + 3\cos \theta  - 2 = 0$

$ \Rightarrow 2{\cos ^2}\theta  + 4\cos \theta  - \cos \theta  - 2 = 0$

$ \Rightarrow 2\cos \theta \left( {\cos \theta  + 2} \right) - 1\left( {\cos \theta  + 2} \right) = 0$

$ \Rightarrow \left( {\cos \theta  + 2} \right)\left( {2\cos \theta  - 1} \right) = 0$

\[ \Rightarrow \cos \theta  + 2 = 0\] or $ \Rightarrow 2\cos \theta  - 1 = 0$

\[ \Rightarrow \cos \theta  \ne  - 2\] $\left[ { - 1 \leqslant \cos \theta  \leqslant 1} \right]$ 

Therefore, $2\cos \theta  - 1 = 0$

\[ \Rightarrow \cos \theta  = \dfrac{1}{2}\]

$ \Rightarrow \cos \theta  = \cos \dfrac{\pi }{3}$ 

$ \Rightarrow \theta  = \dfrac{\pi }{3}$ or $2\pi  - \dfrac{\pi }{3}$

$ \Rightarrow \theta  = \dfrac{\pi }{3}$ or $\dfrac{{5\pi }}{3}$ ( As it is mentioned in the question that $0 \leqslant \theta  \leqslant 2\pi $ )

Therefore, the value of $\theta $ are $\dfrac{\pi }{3}$ and $\dfrac{{5\pi }}{3}$.

19.  If $\sec x\cos 5x + 1 = 0$, where \[0 < x \leqslant \dfrac{\pi }{2}\], then find the value of $x$.

Ans: Given, $\sec x\cos 5x + 1 = 0$

We can also write it as,

$ \Rightarrow \dfrac{1}{{\cos x}}\cos 5x + 1 = 0$

Take LCM

$ \Rightarrow \dfrac{{\cos 5x + \cos x}}{{\cos x}} = 0$

$ \Rightarrow \cos 5x + \cos x = 0$

We know that $\cos C + \cos D = 2\cos \left( {\dfrac{{C + D}}{2}} \right)\cos \left( {\dfrac{{C - D}}{2}} \right)$. Therefore, we get

$ \Rightarrow 2\cos \left( {\dfrac{{5x + x}}{2}} \right)\cos \left( {\dfrac{{5x - x}}{2}} \right) = 0$

$ \Rightarrow \cos \left( {\dfrac{{6x}}{2}} \right)\cos \left( {\dfrac{{4x}}{2}} \right) = 0$

$ \Rightarrow \cos 3x.\cos 2x = 0$

$ \Rightarrow \cos 3x = 0$ or $\cos 2x = 0$

$ \Rightarrow 3x = \dfrac{\pi }{2}$ or $2x = \dfrac{\pi }{2}$

$ \Rightarrow x = \dfrac{\pi }{6}$ or $x = \dfrac{\pi }{4}$

Therefore, the value of $x$ are $\dfrac{\pi }{6}$, $\dfrac{\pi }{4}$.

Long Answer Type

20.  If $\sin \left( {\theta  + \alpha } \right) = a$ and $\sin \left( {\theta  + \beta } \right) = b$, then prove that $\cos 2\left( {\alpha  - \beta } \right) - 4ab\cos \left( {\alpha  - \beta } \right) = 1 - 2{a^2} - 2{b^2}$.

Ans: Given that, $\sin \left( {\theta  + \alpha } \right) = a$ and $\sin \left( {\theta  + \beta } \right) = b$.

We know that $\cos x = \sqrt {1 - {{\sin }^2}x} $. Therefore, we get

$ \Rightarrow \cos \left( {\theta  + \alpha } \right) = \sqrt {1 - {{\left( {\sin \left( {\theta  + \alpha } \right)} \right)}^2}} $ 

$ \Rightarrow \cos \left( {\theta  + \alpha } \right) = \sqrt {1 - {a^2}} $

Similarly, 

$ \Rightarrow \cos \left( {\theta  + \beta } \right) = \sqrt {1 - {{\left( {\sin \left( {\theta  + \beta } \right)} \right)}^2}} $ 

$ \Rightarrow \cos \left( {\theta  + \beta } \right) = \sqrt {1 - {b^2}} $

Now, let us find value of $\cos \left( {\alpha  - \beta } \right)$.

$ \Rightarrow \cos \left( {\alpha  - \beta } \right) = \cos \left[ {\left( {\theta  + \alpha } \right) - \left( {\theta  + \beta } \right)} \right]$ 

We know that $\cos \left( {A - B} \right) = \cos A.\cos B + \sin A.\sin B$. Therefore, we get

$ \Rightarrow \cos \left( {\alpha  - \beta } \right) = \cos \left( {\theta  + \alpha } \right)\cos \left( {\theta  + \beta } \right) + \sin \left( {\theta  + \alpha } \right)\sin \left( {\theta  + \beta } \right)$

On substituting the values, we get

$ \Rightarrow \cos \left( {\alpha  - \beta } \right) = \sqrt {1 - {a^2}} \sqrt {1 - {b^2}}  + ab$

$ \Rightarrow \cos \left( {\alpha  - \beta } \right) = ab + \sqrt {1 - {b^2} - {a^2} + {a^2}{b^2}} $

Now, we will find the value of $\cos 2\left( {\alpha  - \beta } \right)$

We know that $\cos 2A = 2{\cos ^2}A - 1$. Therefore, we get

$ \Rightarrow \cos 2\left( {\alpha  - \beta } \right) = 2{\cos ^2}\left( {\alpha  - \beta } \right) - 1$

\[ \Rightarrow \cos 2\left( {\alpha  - \beta } \right) = 2{\left( {ab + \sqrt {1 - {b^2} - {a^2} + {a^2}{b^2}} } \right)^2} - 1\]

$ \Rightarrow \cos 2\left( {\alpha  - \beta } \right) = 2\left( {{a^2}{b^2} + 1 - {b^2} - {a^2} + {a^2}{b^2} + 2ab\sqrt {1 - {b^2} - {a^2} + {a^2}{b^2}} } \right) - 1$

We have, L.H.S. = $\cos 2\left( {\alpha  - \beta } \right) - 4ab\cos \left( {\alpha  - \beta } \right)$. On substituting the values, we get

$ \Rightarrow 2\left( {{a^2}{b^2} + 1 - {b^2} - {a^2} + {a^2}{b^2} + 2ab\sqrt {1 - {b^2} - {a^2} + {a^2}{b^2}} } \right) - 1 - 4ab\left( {ab + \sqrt {1 - {b^2} - {a^2} + {a^2}{b^2}} } \right)$

$ \Rightarrow 2{a^2}{b^2} + 2 - 2{b^2} - 2{a^2} + 2{a^2}{b^2} + 4ab\sqrt {1 - {b^2} - {a^2} + {a^2}{b^2}}  - 1 - 4{a^2}{b^2} - 4ab\sqrt {1 - {b^2} - {a^2} + {a^2}{b^2}} $

$ \Rightarrow 4{a^2}{b^2} + 1 - 2{a^2} - 2{b^2} + 4ab\sqrt {1 - {b^2} - {a^2} + {a^2}{b^2}}  - 4{a^2}{b^2} - 4ab\sqrt {1 - {b^2} - {a^2} + {a^2}{b^2}} $

On subtraction, we get

$ \Rightarrow 1 - 2{a^2} - 2{b^2}$ 

Hence proved.

21.  If $\cos \left( {\theta  + \phi } \right) = m\cos \left( {\theta  - \phi } \right)$, then prove that $\tan \theta  = \dfrac{{1 - m}}{{1 + m}}\cot \phi $.

Ans: Given, $\cos \left( {\theta  + \phi } \right) = m\cos \left( {\theta  - \phi } \right)$

We can also write it as,

$ \Rightarrow \dfrac{{\cos \left( {\theta  + \phi } \right)}}{{\cos \left( {\theta  - \phi } \right)}} = \dfrac{m}{1}$

Now, we will apply componendo and dividend rule on the above written expression.

$ \Rightarrow \dfrac{{\cos \left( {\theta  + \phi } \right) + \cos \left( {\theta  - \phi } \right)}}{{\cos \left( {\theta  + \phi } \right) - \cos \left( {\theta  - \phi } \right)}} = \dfrac{{m + 1}}{{m - 1}}$

We know that $\cos A - \cos B =  - 2\sin \dfrac{{A + B}}{2}.\sin \dfrac{{A - B}}{2}$ and $\cos A + \cos B = 2\cos \dfrac{{A + B}}{2}.\cos \dfrac{{A - B}}{2}$. Therefore, we get

$ \Rightarrow \dfrac{{2\cos \left( {\dfrac{{\theta  + \phi  + \theta  - \phi }}{2}} \right).\cos \left( {\dfrac{{\theta  + \phi  - \theta  + \phi }}{2}} \right)}}{{ - 2\sin \left( {\dfrac{{\theta  + \phi  + \theta  - \phi }}{2}} \right).\sin \left( {\dfrac{{\theta  + \phi  - \theta  + \phi }}{2}} \right)}} = \dfrac{{m + 1}}{{m - 1}}$

\[ \Rightarrow \dfrac{{2\cos \left( {\dfrac{{2\theta }}{2}} \right).\cos \left( {\dfrac{{2\phi }}{2}} \right)}}{{ - 2\sin \left( {\dfrac{{2\theta }}{2}} \right).\sin \left( {\dfrac{{2\phi }}{2}} \right)}} = \dfrac{{m + 1}}{{m - 1}}\]

On canceling common terms, we get

\[ \Rightarrow \dfrac{{\cos \left( \theta  \right).\cos \left( \phi  \right)}}{{ - \sin \left( \theta  \right).\sin \left( \phi  \right)}} = \dfrac{{m + 1}}{{m - 1}}\]

As we know $\dfrac{{\cos x}}{{\sin x}} = \cot x$. So, we can write above-written equation as,

\[ \Rightarrow  - \cot \theta .\cot \phi  = \dfrac{{m + 1}}{{m - 1}}\]

\[ \Rightarrow  - \dfrac{{\cot \phi }}{{\tan \theta }} = \dfrac{{m + 1}}{{m - 1}}\]

On cross multiplication, we get

\[ \Rightarrow \tan \theta \left( {1 + m} \right) = \cot \phi \left( {1 - m} \right)\]

\[ \Rightarrow \tan \theta  = \dfrac{{\left( {1 - m} \right)}}{{\left( {1 + m} \right)}}\cot \phi \]

Hence proved.

22.  Find  the  value  of  the  expression  $3\left[ {{{\sin }^4}\left( {\dfrac{{3\pi }}{2} - \alpha } \right) + {{\sin }^4}\left( {3\pi  + \alpha } \right)} \right] - 2\left[ {{{\sin }^6}\left( {\dfrac{\pi }{2} + \alpha } \right) + {{\sin }^6}\left( {5\pi  - \alpha } \right)} \right]$ 

Ans: Given, $3\left[ {{{\sin }^4}\left( {\dfrac{{3\pi }}{2} - \alpha } \right) + {{\sin }^4}\left( {3\pi  + \alpha } \right)} \right] - 2\left[ {{{\sin }^6}\left( {\dfrac{\pi }{2} + \alpha } \right) + {{\sin }^6}\left( {5\pi  - \alpha } \right)} \right]$

We can also write it as,

 \[ \Rightarrow 3\left[ {{{\sin }^4}\left( {\dfrac{{3\pi }}{2} - \alpha } \right) + {{\sin }^4}\left( {2\pi  + \left( {\pi  + \alpha } \right)} \right)} \right] - 2\left[ {{{\sin }^6}\left( {\dfrac{\pi }{2} + \alpha } \right) + {{\sin }^6}\left( {4\pi  + \left( {\pi  - \alpha } \right)} \right)} \right]\]

As we know $\sin \left( {\dfrac{{3\pi }}{2} - x} \right) =  - \cos x$, $\sin \left( {2\pi  + x} \right) = \sin x$, $\sin \left( {\dfrac{\pi }{2} + x} \right) = \cos x$ and $\sin \left( {4\pi  + x} \right) = \sin x$. Therefore, we get

\[ \Rightarrow 3\left[ {{{\cos }^4}\alpha  + {{\sin }^4}\left( {\pi  + \alpha } \right)} \right] - 2\left[ {{{\cos }^6}\alpha  + {{\sin }^6}\left( {\pi  - \alpha } \right)} \right]\]

As we know $\sin \left( {\pi  + \alpha } \right) =  - \sin \alpha $ and $\sin \left( {\pi  - \alpha } \right) = \sin \alpha $. Therefore, we get

\[ \Rightarrow 3\left[ {{{\cos }^4}\alpha  + {{\sin }^4}\alpha } \right] - 2\left[ {{{\cos }^6}\alpha  + {{\sin }^6}\alpha } \right]\]

\[ \Rightarrow 3\left[ {{{\left( {{{\cos }^2}\alpha } \right)}^2} + {{\left( {{{\sin }^2}\alpha } \right)}^2}} \right] - 2\left[ {{{\left( {{{\cos }^2}\alpha } \right)}^3} + {{\left( {{{\sin }^2}\alpha } \right)}^3}} \right]..........\left( i \right)\]

As we know ${\left( {a + b} \right)^2} = {a^2} + {b^2} + 2ab$. Therefore, we can write \[{\left( {{{\cos }^2}\alpha } \right)^2} + {\left( {{{\sin }^2}\alpha } \right)^2}\] as \[{\left( {{{\cos }^2}\alpha  + {{\sin }^2}\alpha } \right)^2} - 2{\cos ^2}\alpha {\sin ^2}\alpha \]. From here we can conclude that \[\left( {{{\cos }^4}\alpha } \right) + \left( {{{\sin }^4}\alpha } \right) = {\left( {{{\cos }^2}\alpha  + {{\sin }^2}\alpha } \right)^2} - 2{\cos ^2}\alpha {\sin ^2}\alpha ..........\left( {ii} \right)\]

Also, as we know ${a^3} + {b^3} = \left( {a + b} \right)\left( {{a^2} + {b^2} - ab} \right)$. Therefore, we can write on expansion of  \[{\left( {{{\cos }^2}\alpha } \right)^3} + {\left( {{{\sin }^2}\alpha } \right)^3}\], we get \[\left( {{{\cos }^2}\alpha  + {{\sin }^2}\alpha } \right)\left( {{{\cos }^4}\alpha  + {{\sin }^4}\alpha  - {{\cos }^2}\alpha {{\sin }^2}\alpha } \right)\].

Now, we will substitute these value in equation $\left( i \right)$.

\[ \Rightarrow 3\left[ {{{\left( {{{\cos }^2}\alpha  + {{\sin }^2}\alpha } \right)}^2} - 2{{\cos }^2}\alpha {{\sin }^2}\alpha } \right] - 2\left[ {\left( {{{\cos }^2}\alpha  + {{\sin }^2}\alpha } \right)\left( {{{\cos }^4}\alpha  + {{\sin }^4}\alpha  - {{\cos }^2}\alpha {{\sin }^2}\alpha } \right)} \right]\]

As we know ${\sin ^2}x + {\cos ^2}x = 1$. Therefore, we get

\[ \Rightarrow 3\left( {1 - 2{{\cos }^2}\alpha {{\sin }^2}\alpha } \right) - 2\left( {{{\cos }^4}\alpha  + {{\sin }^4}\alpha  - {{\cos }^2}\alpha {{\sin }^2}\alpha } \right)\]

From $\left( {ii} \right)$, we get

\[ \Rightarrow 3\left( {1 - 2{{\cos }^2}\alpha {{\sin }^2}\alpha } \right) - 2\left( {{{\left( {{{\cos }^2}\alpha  + {{\sin }^2}\alpha } \right)}^2} - 2{{\cos }^2}\alpha {{\sin }^2}\alpha  - {{\cos }^2}\alpha {{\sin }^2}\alpha } \right)\]

As we know ${\sin ^2}x + {\cos ^2}x = 1$. Therefore, we get

\[ \Rightarrow 3\left( {1 - 2{{\cos }^2}\alpha {{\sin }^2}\alpha } \right) - 2\left( {1 - 2{{\cos }^2}\alpha {{\sin }^2}\alpha  - {{\cos }^2}\alpha {{\sin }^2}\alpha } \right)\]

\[ \Rightarrow 3\left( {1 - 2{{\cos }^2}\alpha {{\sin }^2}\alpha } \right) - 2\left( {1 - 3{{\cos }^2}\alpha {{\sin }^2}\alpha } \right)\]

On multiplication, we get

\[ \Rightarrow 3 - 6{\cos ^2}\alpha {\sin ^2}\alpha  - 2 + 6{\cos ^2}\alpha {\sin ^2}\alpha \]

On subtraction, we get

\[ \Rightarrow 1\]

Hence, value of $3\left[ {{{\sin }^4}\left( {\dfrac{{3\pi }}{2} - \alpha } \right) + {{\sin }^4}\left( {3\pi  + \alpha } \right)} \right] - 2\left[ {{{\sin }^6}\left( {\dfrac{\pi }{2} + \alpha } \right) + {{\sin }^6}\left( {5\pi  - \alpha } \right)} \right]$ is $1$.

23.  If $a\cos 2\theta  + b\sin 2\theta  = c$ has $\alpha $ and $\beta $ as its roots, then prove that $\tan \alpha  + \tan \beta  = \dfrac{{2b}}{{a + c}}$.

Ans: Given, $a\cos 2\theta  + b\sin 2\theta  = c$ has $\alpha $ and $\beta $ as its roots.

Let $a\cos 2\theta  + b\sin 2\theta  = c$ be equation $\left( i \right)$.

We know that $\cos 2x = \dfrac{{1 - {{\tan }^2}x}}{{1 + {{\tan }^2}x}}$ and  $\sin 2x = \dfrac{{2\tan x}}{{1 + {{\tan }^2}x}}$. Therefore, we get

$ \Rightarrow a\left( {\dfrac{{1 - {{\tan }^2}\theta }}{{1 + {{\tan }^2}\theta }}} \right) + b\left( {\dfrac{{2\tan \theta }}{{1 + {{\tan }^2}\theta }}} \right) = c$

Take LCM

$ \Rightarrow \dfrac{{a\left( {1 - {{\tan }^2}\theta } \right) + b\left( {2\tan \theta } \right)}}{{1 + {{\tan }^2}\theta }} = c$

On cross multiplication, we get

$ \Rightarrow a\left( {1 - {{\tan }^2}\theta } \right) + b\left( {2\tan \theta } \right) = c\left( {1 + {{\tan }^2}\theta } \right)$

On multiplication of terms, we get

$ \Rightarrow a - a{\tan ^2}\theta  + 2b\tan \theta  = c + c{\tan ^2}\theta $

$ \Rightarrow a - a{\tan ^2}\theta  + 2b\tan \theta  - c - c{\tan ^2}\theta  = 0$

Divide whole equation by $ - 1$.

$ \Rightarrow  - a + a{\tan ^2}\theta  - 2b\tan \theta  + c + c{\tan ^2}\theta  = 0$

$ \Rightarrow \left( {a + c} \right){\tan ^2}\theta  - 2b\tan \theta  + \left( {c - a} \right) = 0.......\left( {ii} \right)$

We are given that $\alpha $ and $\beta $ are the roots of equation $\left( i \right)$. Thus,  $\tan \alpha $ and $\tan \beta $ are the roots of the equation $\left( {ii} \right)$.

As we know sum of roots of a quadratic equation $a{x^2} + bx + c = 0$ is $\dfrac{{ - b}}{a}$. Therefore, we get

$ \Rightarrow \tan \alpha  + \tan \beta  = \dfrac{{ - \left( { - 2b} \right)}}{{a + c}}$ 

$ \Rightarrow \tan \alpha  + \tan \beta  = \dfrac{{2b}}{{a + c}}$

Hence proved.

24.  If $x = \sec \phi  - \tan \phi $ and $y = \cos ec\phi  + \cot \phi $ then show that $xy + x - y + 1 = 0$.

Ans: Given, $x = \sec \phi  - \tan \phi $ and $y = \cos ec\phi  + \cot \phi $

We have, L.H.S. = $xy + x - y + 1$.

Now, we will substitute the given values in above written expression.

$ \Rightarrow \left( {\sec \phi  - \tan \phi } \right)\left( {\cos ec\phi  + \cot \phi } \right) + \left( {\sec \phi  - \tan \phi } \right) - \left( {\cos ec\phi  + \cot \phi } \right) + 1$

Now, we will write above written expression in terms of $\sin $ and $\cos $.

\[ \Rightarrow \left( {\dfrac{{1 - \sin \phi }}{{\cos \phi }}} \right)\left( {\dfrac{{1 + \cos \phi }}{{\sin \phi }}} \right) + \left( {\dfrac{{1 - \sin \phi }}{{\cos \phi }}} \right) - \left( {\dfrac{{1 + \cos \phi }}{{\sin \phi }}} \right) + 1\]

\[ \Rightarrow \dfrac{{\left( {1 - \sin \phi } \right)\left( {1 + \cos \phi } \right)}}{{\cos \phi \sin \phi }} + \left( {\dfrac{{\sin \phi \left( {1 - \sin \phi } \right) - \cos \phi \left( {1 + \cos \phi } \right)}}{{\cos \phi \sin \phi }}} \right) + 1\]

\[ \Rightarrow \dfrac{{1 - \sin \phi  + \cos \phi  - \sin \phi \cos \phi }}{{\cos \phi \sin \phi }} + \left( {\dfrac{{\sin \phi  - {{\sin }^2}\phi  - \cos \phi  - {{\cos }^2}\phi }}{{\cos \phi \sin \phi }}} \right) + 1\]

\[ \Rightarrow \dfrac{{1 - \sin \phi  + \cos \phi  - \sin \phi \cos \phi  + \sin \phi  - \cos \phi  - \left( {{{\sin }^2}\phi  + {{\cos }^2}\phi } \right) + \sin \phi \cos \phi }}{{\cos \phi \sin \phi }}\]

We know that ${\sin ^2}x + {\cos ^2}x = 1$. Therefore, we get

\[ \Rightarrow \dfrac{{1 - 1}}{{\cos \phi \sin \phi }} = 0\]

Hence proved.

25.  If $\theta $ lies in the first quadrant and $\cos \theta  = \dfrac{8}{{17}}$, then find the value of $\cos \left( {30^\circ  + \theta } \right) + \cos \left( {45^\circ  - \theta } \right) + \cos \left( {120^\circ  - \theta } \right)$.

Ans: Here, we are given that $\cos \theta  = \dfrac{8}{{17}}$, $\theta $ lies in the first quadrant. 

We know that $\sin x = \sqrt {1 - {{\cos }^2}x} $. Therefore, we get

$ \Rightarrow \sin \theta  = \sqrt {1 - {{\left( {\dfrac{8}{{17}}} \right)}^2}} $ 

$ \Rightarrow \sin \theta  = \sqrt {1 - \dfrac{{64}}{{289}}} $

$ \Rightarrow \sin \theta  = \sqrt {\dfrac{{289 - 64}}{{289}}} $

$ \Rightarrow \sin \theta  = \sqrt {\dfrac{{225}}{{289}}} $

\[ \Rightarrow \sin \theta  =  \pm \dfrac{{15}}{{17}}\]

But $\theta $ lies in the first quadrant and in first quadrant $\sin e$ is positive.

\[ \Rightarrow \sin \theta  = \dfrac{{15}}{{17}}\]

We need to find the value of $\cos \left( {30^\circ  + \theta } \right) + \cos \left( {45^\circ  - \theta } \right) + \cos \left( {120^\circ  - \theta } \right)$.

We know that $\cos \left( {A + B} \right) = \cos A\cos B - \sin A\sin B$ and $\cos \left( {A - B} \right) = \cos A\cos B + \sin A\sin B$. Therefore, we get

$ \Rightarrow \cos 30^\circ \cos \theta  - \sin 30^\circ \sin \theta  + \cos 45^\circ \cos \theta  + \sin 45^\circ \sin \theta  + \cos 120^\circ \cos \theta  + \sin 120^\circ \sin \theta $

Substitute value of $\cos 30^\circ  = \dfrac{{\sqrt 3 }}{2}$, $\sin 30^\circ  = \dfrac{1}{2}$, $\cos 45^\circ  = \dfrac{1}{{\sqrt 2 }}$, $\sin 45^\circ  = \dfrac{1}{{\sqrt 2 }}$, $\cos 120^\circ  =  - \dfrac{1}{2}$ and $\sin 120^\circ  = \dfrac{{\sqrt 3 }}{2}$.

$ \Rightarrow \dfrac{{\sqrt 3 }}{2} \times \cos \theta  - \dfrac{1}{2} \times \sin \theta  + \dfrac{1}{{\sqrt 2 }} \times \cos \theta  + \dfrac{1}{{\sqrt 2 }} \times \sin \theta  - \dfrac{1}{2}\cos \theta  + \dfrac{{\sqrt 3 }}{2}\sin \theta $

$ \Rightarrow \dfrac{{\sqrt 3 }}{2}\left( {\cos \theta  + \sin \theta } \right) - \dfrac{1}{2}\left( {\cos \theta  + \sin \theta } \right) + \dfrac{1}{{\sqrt 2 }}\left( {\cos \theta  + \sin \theta } \right)$

$ \Rightarrow \left( {\dfrac{{\sqrt 3 }}{2} - \dfrac{1}{2} + \dfrac{1}{{\sqrt 2 }}} \right)\left( {\cos \theta  + \sin \theta } \right)$

$ \Rightarrow \left( {\dfrac{{\sqrt 3  - 1}}{2} + \dfrac{1}{{\sqrt 2 }}} \right)\left( {\dfrac{8}{{17}} + \dfrac{{15}}{{17}}} \right)$

$ \Rightarrow \left( {\dfrac{{\sqrt 3  - 1 + \sqrt 2 }}{2}} \right)\left( {\dfrac{{23}}{{17}}} \right)$

$ \Rightarrow \dfrac{{23}}{{34}}\left( {\sqrt 3  - 1 + \sqrt 2 } \right)$

This is our required answer.

26.  Find the value of the expression ${\cos ^4}\dfrac{\pi }{8} + {\cos ^4}\dfrac{{3\pi }}{8} + {\cos ^4}\dfrac{{5\pi }}{8} + {\cos ^4}\dfrac{{7\pi }}{8}$.

Ans: Given expression, ${\cos ^4}\dfrac{\pi }{8} + {\cos ^4}\dfrac{{3\pi }}{8} + {\cos ^4}\dfrac{{5\pi }}{8} + {\cos ^4}\dfrac{{7\pi }}{8}$

This can also be written as,

$ \Rightarrow {\cos ^4}\dfrac{\pi }{8} + {\cos ^4}\dfrac{{3\pi }}{8} + {\cos ^4}\left( {\pi  - \dfrac{{3\pi }}{8}} \right) + {\cos ^4}\left( {\pi  - \dfrac{\pi }{8}} \right)$

We know that $\cos \left( {\pi  - \theta } \right) =  - \cos \theta $. Therefore, we get

$ \Rightarrow {\cos ^4}\dfrac{\pi }{8} + {\cos ^4}\dfrac{{3\pi }}{8} + {\cos ^4}\dfrac{{3\pi }}{8} + {\cos ^4}\dfrac{\pi }{8}$

(Here, ${\cos ^4}\dfrac{{3\pi }}{8}$, ${\cos ^4}\dfrac{\pi }{8}$ are positive because power is even)

$ \Rightarrow 2{\cos ^4}\dfrac{\pi }{8} + 2{\cos ^4}\dfrac{{3\pi }}{8}$

$ \Rightarrow 2\left[ {{{\cos }^4}\dfrac{\pi }{8} + {{\cos }^4}\dfrac{{3\pi }}{8}} \right]$

$ \Rightarrow 2\left[ {{{\cos }^4}\dfrac{\pi }{8} + {{\cos }^4}\left( {\dfrac{\pi }{2} - \dfrac{\pi }{8}} \right)} \right]$

We know that $\cos \left( {\dfrac{\pi }{2} - \theta } \right) = \sin \theta $. Therefore, we get

$ \Rightarrow 2\left[ {{{\cos }^4}\dfrac{\pi }{8} + {{\sin }^4}\dfrac{\pi }{8}} \right]$

We know that ${a^2} + {b^2} = {\left( {a + b} \right)^2} - 2ab$. Therefore, we get

$ \Rightarrow 2\left[ {{{\left( {{{\cos }^2}\dfrac{\pi }{8} + {{\sin }^2}\dfrac{\pi }{8}} \right)}^2} - 2{{\sin }^2}\dfrac{\pi }{8} \times {{\cos }^2}\dfrac{\pi }{8}} \right]$

$ \Rightarrow 2\left[ {1 - 2{{\sin }^2}\dfrac{\pi }{8} \times {{\cos }^2}\dfrac{\pi }{8}} \right]$

$ \Rightarrow 2 - 4{\sin ^2}\dfrac{\pi }{8} \times {\cos ^2}\dfrac{\pi }{8}$

$ \Rightarrow 2 - {\left( {2\sin \dfrac{\pi }{8} \times \cos \dfrac{\pi }{8}} \right)^2}$

We know that $\sin 2x = 2\sin x\cos x$. Therefore, we get

$ \Rightarrow 2 - {\left( {\sin \dfrac{\pi }{4}} \right)^2}$

Substitute $\sin \dfrac{\pi }{4} = \dfrac{1}{{\sqrt 2 }}$.

$ \Rightarrow 2 - {\left( {\dfrac{1}{{\sqrt 2 }}} \right)^2}$

$ \Rightarrow 2 - \dfrac{1}{2} = \dfrac{{4 - 1}}{2}$

$ \Rightarrow \dfrac{3}{2}$

Therefore, value of given expression is $\dfrac{3}{2}$.

27.  Find the general solution of the equation $5{\cos ^2}\theta  + 7{\sin ^2}\theta  - 6 = 0$.

Ans: Given, $5{\cos ^2}\theta  + 7{\sin ^2}\theta  - 6 = 0$

We know that ${\sin ^2}x = 1 - {\cos ^2}x$. Therefore, we get

$ \Rightarrow 5{\cos ^2}\theta  + 7\left( {1 - {{\cos }^2}x} \right) - 6 = 0$

$ \Rightarrow 5{\cos ^2}\theta  + 7 - 7{\cos ^2}x - 6 = 0$

$ \Rightarrow 1 - 2{\cos ^2}x = 0$

$ \Rightarrow 2{\cos ^2}x = 1$

$ \Rightarrow {\cos ^2}x = \dfrac{1}{2}$

$ \Rightarrow {\cos ^2}x = \cos \dfrac{\pi }{4}$

We know that $1 + \cos 2x = 2{\cos ^2}x$. Therefore, we get

$ \Rightarrow \dfrac{{1 + \cos 2\theta }}{2} = \dfrac{{1 + \cos 2 \times \dfrac{\pi }{4}}}{2}$

$ \Rightarrow 1 + \cos 2\theta  = 1 + \cos \dfrac{\pi }{2}$

$ \Rightarrow \cos 2\theta  = \cos \dfrac{\pi }{2}$

We know that if $\cos \theta  = \cos \alpha $ then $\theta  = 2n\pi  \pm \alpha $, $n \in Z$

$ \Rightarrow 2\theta  = 2n\pi  \pm \dfrac{\pi }{2}$

$ \Rightarrow \theta  = n\pi  \pm \dfrac{\pi }{4}$

Therefore, the general solution given equation is $\theta  = n\pi  \pm \dfrac{\pi }{4}$ where $n \in Z$.

28.  Find the general solution of the equation $\sin x - 3\sin 2x + \sin 3x = \cos x - 3\cos 2x + \cos 3x$.

Ans: Given equation, $\sin x - 3\sin 2x + \sin 3x = \cos x - 3\cos 2x + \cos 3x$

$ \Rightarrow \left( {\sin 3x + \sin x} \right) - 3\sin 2x = \left( {\cos 3x + \cos x} \right) - 3\cos 2x$

We know that $\sin A + \sin B = 2\sin \dfrac{{A + B}}{2}\cos \dfrac{{A - B}}{2}$ and $\cos A + \cos B = 2\cos \dfrac{{A + B}}{2}\cos \dfrac{{A - B}}{2}$. Therefore, we get

$ \Rightarrow 2\sin \dfrac{{3x + x}}{2}\cos \dfrac{{3x - x}}{2} - 3\sin 2x = 2\cos \dfrac{{3x + x}}{2}\cos \dfrac{{3x - x}}{2} - 3\cos 2x$

$ \Rightarrow 2\sin 2x.\cos x - 3\sin 2x = 2\cos 2x.\cos x - 3\cos 2x$

$ \Rightarrow 2\cos x\left( {\sin 2x - \cos 2x} \right) = 3\left( {\sin 2x - \cos 2x} \right)$

$ \Rightarrow 2\cos x\left( {\sin 2x - \cos 2x} \right) - 3\left( {\sin 2x - \cos 2x} \right) = 0$

$ \Rightarrow \left( {\sin 2x - \cos 2x} \right)\left( {2\cos x - 3} \right) = 0$

$ \Rightarrow \sin 2x - \cos 2x = 0$ or $ \Rightarrow 2\cos x - 3 \ne 0$ ( $ - 1 \leqslant \cos x \leqslant 1$ )

$ \Rightarrow \sin 2x = \cos 2x$

$ \Rightarrow \dfrac{{\sin 2x}}{{\cos 2x}} = 1$

$ \Rightarrow \tan 2x = 1$

We know that if $\tan \theta  = \tan \alpha $ then $\theta  = n\pi  + \alpha $, $n \in Z$

$ \Rightarrow \tan 2x = \tan \dfrac{\pi }{4}$

$ \Rightarrow 2x = n\pi  + \dfrac{\pi }{4}$

$ \Rightarrow x = \dfrac{{n\pi }}{2} + \dfrac{\pi }{8}$

Therefore, the general solution given equation is $x = \dfrac{{n\pi }}{2} + \dfrac{\pi }{8}$ where $n \in Z$.

29.  Find the general solution of the equation $\left( {\sqrt 3  - 1} \right)\cos \theta  + \left( {\sqrt 3  + 1} \right)\sin \theta  = 2$.

Ans: Given, $\left( {\sqrt 3  - 1} \right)\cos \theta  + \left( {\sqrt 3  + 1} \right)\sin \theta  = 2$

Put $\sqrt 3  - 1 = r\sin \alpha ......\left( i \right)$ and $\sqrt 3  + 1 = r\cos \alpha ......\left( {ii} \right)$

On squaring and adding both the sides, we get

\[ \Rightarrow {\left( {r\sin \alpha } \right)^2} + {\left( {r\cos \alpha } \right)^2} = {\left( {\sqrt 3  - 1} \right)^2} + {\left( {\sqrt 3  + 1} \right)^2}\]

\[ \Rightarrow {r^2}{\sin ^2}\alpha  + {r^2}{\cos ^2}\alpha  = 3 + 1 - 2\sqrt 3  + 3 + 1 + 2\sqrt 3 \]

\[ \Rightarrow {r^2}\left( {{{\sin }^2}\alpha  + {{\cos }^2}\alpha } \right) = 8\]

We know that ${\sin ^2}x + {\cos ^2}x = 1$. Therefore, we get

\[ \Rightarrow {r^2} = 8\]

\[ \Rightarrow r = 2\sqrt 2 \]

The given equation can be written as,

$ \Rightarrow r\sin \alpha .\cos \theta  + r\cos \alpha .\sin \theta  = 2$

$ \Rightarrow r\left( {\sin \alpha .\cos \theta  + \cos \alpha .\sin \theta } \right) = 2$

We know that $\sin \left( {A + B} \right) = \sin A\cos B + \cos A\sin B$. Therefore, we get

$ \Rightarrow 2\sqrt 2 \sin \left( {\alpha  + \theta } \right) = 2$

$ \Rightarrow \sqrt 2 \sin \left( {\alpha  + \theta } \right) = 1$

$ \Rightarrow \sin \left( {\alpha  + \theta } \right) = \dfrac{1}{{\sqrt 2 }}$

$ \Rightarrow \sin \left( {\alpha  + \theta } \right) = \sin \dfrac{\pi }{4}$

We know that if $\sin \theta  = \sin \alpha $ then $\theta  = n\pi  + {\left( { - 1} \right)^n}\alpha $, $n \in Z$

$ \Rightarrow \alpha  + \theta  = n\pi  + {\left( { - 1} \right)^n}.\dfrac{\pi }{4}.......\left( {iii} \right)$

We have, $\dfrac{{r\sin \alpha }}{{r\cos \alpha }} = \dfrac{{\sqrt 3  - 1}}{{\sqrt 3  + 1}}$ from equation $\left( i \right)$ and $\left( {ii} \right)$.

This can also be written as, $\tan \alpha  = \dfrac{{\sqrt 3  - 1}}{{1 + \sqrt 3 .1}}$

We know that $\tan \dfrac{\pi }{3} = \sqrt 3 $ and $\tan \dfrac{\pi }{4} = 1$. Therefore, we get

$ \Rightarrow \tan \alpha  = \dfrac{{\tan \dfrac{\pi }{3} - \tan \dfrac{\pi }{4}}}{{1 + \tan \dfrac{\pi }{3}.\tan \dfrac{\pi }{4}}}$

We know that $\tan \left( {x - y} \right) = \dfrac{{\tan x - \tan y}}{{1 + \tan x.\tan y}}$. Therefore, we get

$ \Rightarrow \tan \alpha  = \tan \left( {\dfrac{\pi }{3} - \dfrac{\pi }{4}} \right)$

$ \Rightarrow \tan \alpha  = \tan \dfrac{\pi }{{12}}$

$ \Rightarrow \alpha  = \dfrac{\pi }{{12}}$

Now, we will substitute value of $\alpha $, in equation $\left( {iii} \right)$.

$ \Rightarrow \dfrac{\pi }{{12}} + \theta  = n\pi  + {\left( { - 1} \right)^n}.\dfrac{\pi }{4}$

$ \Rightarrow \theta  = n\pi  + {\left( { - 1} \right)^n}.\dfrac{\pi }{4} - \dfrac{\pi }{{12}}$

Therefore, the general solution given equation is $\theta  = n\pi  + {\left( { - 1} \right)^n}.\dfrac{\pi }{4} - \dfrac{\pi }{{12}}$ where $n \in Z$.

OBJECTIVE TYPE QUESTIONS

Choose the correct answer from the given options in the exercises $30$ to $59$.

30.  If $\sin \theta  + \cos ec\theta  = 2$, then ${\sin ^2}\theta  + \cos e{c^2}\theta $ is equal to

1. $1$ 

2. $4$ 

3. $2$ 

4. None of these

Ans: Given, $\sin \theta  + \cos ec\theta  = 2$ 

On squaring both the sides, we get

$ \Rightarrow {\left( {\sin \theta  + \cos ec\theta } \right)^2} = {2^2}$ 

We know that ${\left( {a + b} \right)^2} = {a^2} + {b^2} + 2ab$. Therefore, we get

\[ \Rightarrow {\sin ^2}\theta  + \cos e{c^2}\theta  + 2\sin \theta \cos ec\theta  = 4\]

\[ \Rightarrow {\sin ^2}\theta  + \cos e{c^2}\theta  + 2\sin \theta \dfrac{1}{{\sin \theta }} = 4\]

On canceling common terms, we get

\[ \Rightarrow {\sin ^2}\theta  + \cos e{c^2}\theta  + 2 = 4\]

Transport $2$ to the RHS

\[ \Rightarrow {\sin ^2}\theta  + \cos e{c^2}\theta  = 4 - 2\]

\[ \Rightarrow {\sin ^2}\theta  + \cos e{c^2}\theta  = 2\]

Hence, option (c) is the correct answer.

31.  If $f\left( x \right) = {\cos ^2}x + {\sec ^2}x$, then 

1. $f\left( x \right) < 1$ 

2. $f\left( x \right) = 1$ 

3. $2 < f\left( x \right) < 1$ 

4. $f\left( x \right) \geqslant 2$ 

Ans: Given, $f\left( x \right) = {\cos ^2}x + {\sec ^2}x$

As we know $AM \geqslant GM$. Therefore, we get

$ \Rightarrow \dfrac{{{{\cos }^2}x + {{\sec }^2}x}}{2} \geqslant \sqrt {{{\cos }^2}x \times {{\sec }^2}x} $

We know that $\cos x = \dfrac{1}{{\sec x}}$. Therefore, we get

$ \Rightarrow \dfrac{{{{\cos }^2}x + {{\sec }^2}x}}{2} \geqslant 1$

On cross multiplication, we get

$ \Rightarrow {\cos ^2}x + {\sec ^2}x \geqslant 2$

$ \Rightarrow f\left( x \right) \geqslant 2$

Hence, option (d) is the correct answer.

32.  If $\tan \theta  = \dfrac{1}{2}$ and $\tan \phi  = \dfrac{1}{3}$, then the value of $\theta  + \phi $ is 

1. $\dfrac{\pi }{6}$ 

2. $\pi $ 

3. $0$ 

4. $\dfrac{\pi }{4}$ 

Ans: Given, $\tan \theta  = \dfrac{1}{2}$ and $\tan \phi  = \dfrac{1}{3}$

We know that $\tan \left( {\theta  + \phi } \right) = \dfrac{{\tan \theta  + \tan \phi }}{{1 - \tan \theta \tan \phi }}$. Therefore, we will substitute the given values in this formula.

$ \Rightarrow \tan \left( {\theta  + \phi } \right) = \dfrac{{\dfrac{1}{2} + \dfrac{1}{3}}}{{1 - \dfrac{1}{2} \times \dfrac{1}{3}}}$

On taking LCM, we get

$ \Rightarrow \tan \left( {\theta  + \phi } \right) = \dfrac{{\dfrac{{3 + 2}}{6}}}{{\dfrac{{6 - 1}}{6}}}$

$ \Rightarrow \tan \left( {\theta  + \phi } \right) = \dfrac{{\dfrac{5}{6}}}{{\dfrac{5}{6}}} = 1$

As we know $\tan \dfrac{\pi }{4} = 1$. Therefore, we get

$ \Rightarrow \tan \left( {\theta  + \phi } \right) = \tan \dfrac{\pi }{4}$

$ \Rightarrow \theta  + \phi  = \dfrac{\pi }{4}$

Hence, option (d) is the correct answer.

33.  Which of the following is not correct?

1. $\sin \theta  =  - \dfrac{1}{5}$ 

2. $\cos \theta  = 1$ 

3. $\sec \theta  = \dfrac{1}{2}$ 

4. $\tan \theta  = 20$ 

Ans: 

As we know $ - 1 \leqslant \sin \theta  \leqslant 1$. Therefore, $\sin \theta  =  - \dfrac{1}{5}$ is correct. 

We know that $\cos 0^\circ  = 1$. Therefore, $\cos \theta  = 1$ is correct.

We have, $\sec \theta  = \dfrac{1}{2}$. This can also be written as

$ \Rightarrow \cos \theta  = 2$

Which is not correct because $ - 1 \leqslant \sin \theta  \leqslant 1$.

Hence, option (d) is the correct answer.

34. The value of $\tan 1^\circ \tan 2^\circ \tan 3^\circ .....\tan 89^\circ $ is

1. $0$ 

2. $1$ 

3. $\dfrac{1}{2}$ 

4. Not defined

Ans: We need to find the value of $\tan 1^\circ \tan 2^\circ \tan 3^\circ .....\tan 89^\circ $

$ \Rightarrow \tan 1^\circ \tan 2^\circ .....\tan 44^\circ \tan 45^\circ \tan \left( {90^\circ  - 44^\circ } \right).......\tan \left( {90^\circ  - 2^\circ } \right)\tan \left( {90^\circ  - 1^\circ } \right)$

We know that $\tan \left( {90^\circ  - \theta } \right) = \cot \theta $. Therefore, we get

\[ \Rightarrow \left[ {\tan 1^\circ \tan 2^\circ .....\tan 44^\circ } \right]\tan 45^\circ \left[ {\cot 44^\circ ......\cot 2^\circ .\cot 1^\circ } \right]\]

$ \Rightarrow \left[ {\left( {\tan 1^\circ  \times \cot 1^\circ } \right)\left( {\tan 2^\circ \cot 2^\circ } \right).....\left( {\tan 44^\circ \cot 44^\circ } \right)} \right] \times \tan 45^\circ $

We know that $\tan A \times \cot A = 1$. Therefore, we get

$ \Rightarrow 1 \times 1... \times 1 \times \tan 45^\circ $

Substitute value of $\tan 45^\circ  = 1$.

$ \Rightarrow 1 \times 1... \times 1 \times 1 = 1$

Hence, option (b) is the correct answer.

35.  The value of $\dfrac{{1 - {{\tan }^2}15^\circ }}{{1 + {{\tan }^2}15^\circ }}$ is

1. $1$ 

2. $\sqrt 3 $ 

3. $\dfrac{{\sqrt 3 }}{2}$ 

4. $2$ 

Ans: We have to find the value of $\dfrac{{1 - {{\tan }^2}15^\circ }}{{1 + {{\tan }^2}15^\circ }}$

Let $\theta  = 15^\circ $ 

$ \Rightarrow 2\theta  = 30^\circ $ 

As we know $\cos 2\theta  = \dfrac{{1 - {{\tan }^2}\theta }}{{1 + {{\tan }^2}\theta }}$. Therefore, on substituting value of $\theta $ we get

$ \Rightarrow \cos 30^\circ  = \dfrac{{1 - {{\tan }^2}15^\circ }}{{1 + {{\tan }^2}15^\circ }}$

Substitute value of $\tan 30^\circ  = \dfrac{{\sqrt 3 }}{2}$.

$ \Rightarrow \dfrac{{\sqrt 3 }}{2} = \dfrac{{1 - {{\tan }^2}15^\circ }}{{1 + {{\tan }^2}15^\circ }}$

Or

$ \Rightarrow \dfrac{{1 - {{\tan }^2}15^\circ }}{{1 + {{\tan }^2}15^\circ }} = \dfrac{{\sqrt 3 }}{2}$

Hence, option (c) is the correct answer.

36.  The value of $\cos 1^\circ \cos 2^\circ \cos 3^\circ .....\cos 179^\circ $ is

1. $\dfrac{1}{{\sqrt 2 }}$ 

2. $0$ 

3. $1$ 

4. $ - 1$ 

Ans: Given expression: $\cos 1^\circ \cos 2^\circ \cos 3^\circ .....\cos 179^\circ $

$ \Rightarrow \cos 1^\circ \cos 2^\circ \cos 3^\circ .....\cos 90^\circ ......\cos 179^\circ $

As we know $\cos 90^\circ  = 0$. Therefore, we get

$ \Rightarrow \cos 1^\circ \cos 2^\circ \cos 3^\circ ..... \times 0 \times ......\cos 179^\circ $

$ \Rightarrow 0$

Hence, option (b) is the correct answer.

37.  If $\tan \theta  = 3$ and $\theta $ lies in third quadrant, then the value of $\sin \theta $ is

1. $\dfrac{1}{{\sqrt {10} }}$ 

2. $ - \dfrac{1}{{\sqrt {10} }}$ 

3. $\dfrac{{ - 3}}{{\sqrt {10} }}$ 

4. $\dfrac{3}{{\sqrt {10} }}$ 

Ans: Given, $\tan \theta  = 3$

$ \Rightarrow \tan \theta  = \dfrac{P}{B} = \dfrac{3}{1}$ 

$ \Rightarrow H = \sqrt {{3^2} + {1^2}} $ 

$ \Rightarrow H = \sqrt {9 + 1} $

$ \Rightarrow H = \sqrt {10} $

$ \Rightarrow \sin \theta  =  - \dfrac{3}{{\sqrt {10} }}$ 

( The value of $\sin \theta $ is negative because $\theta $ lies in the third quadrant )

Hence, option (a) is the correct answer.

38.  The value of $\tan 75^\circ  - \cot 75^\circ $ is equal to

1. $2\sqrt 3 $ 

2. $2 + \sqrt 3 $ 

3. $2 - \sqrt 3 $ 

4. $1$ 

Ans: Given expression, $\tan 75^\circ  - \cot 75^\circ $

Above written expression can also be written as,

\[ \Rightarrow \tan 75^\circ  - \cot \left( {90^\circ  - 15^\circ } \right)\]

We know that $\cot \left( {90^\circ  - \theta } \right) = \tan \theta $. Therefore, we get

\[ \Rightarrow \tan 75^\circ  - \tan 15^\circ \]

\[ \Rightarrow \dfrac{{\sin 75^\circ }}{{\cos 75^\circ }} - \dfrac{{\sin 15^\circ }}{{\cos 15^\circ }}\]

Take LCM

\[ \Rightarrow \dfrac{{\sin 75^\circ \cos 15^\circ  - \cos 75^\circ \sin 15^\circ }}{{\cos 75^\circ \cos 15^\circ }}\]

We know that $\sin \left( {A - B} \right) = \sin A\cos B - \cos A\sin B$. Therefore, we get

\[ \Rightarrow \dfrac{{\sin \left( {75^\circ  - 15^\circ } \right)}}{{\cos 75^\circ \cos 15^\circ }}\]

\[ \Rightarrow \dfrac{{\sin \left( {75^\circ  - 15^\circ } \right)}}{{\dfrac{1}{2} \times 2\cos 75^\circ \cos 15^\circ }}\]

We know that $2\cos A\cos B = \cos \left( {A + B} \right) + \cos \left( {A - B} \right)$. Therefore, we get

\[ \Rightarrow \dfrac{{2\sin \left( {75^\circ  - 15^\circ } \right)}}{{\cos \left( {75^\circ  + 15^\circ } \right) + \cos \left( {75^\circ  - 15^\circ } \right)}}\]

\[ \Rightarrow \dfrac{{2\sin 60^\circ }}{{\cos 90^\circ  + \cos 60^\circ }}\]

On substituting the values, we get

\[ \Rightarrow \dfrac{{2 \times \dfrac{{\sqrt 3 }}{2}}}{{0 + \dfrac{1}{2}}}\]

\[ \Rightarrow \dfrac{{\sqrt 3 }}{{0 + \dfrac{1}{2}}} = 2\sqrt 3 \]

Hence, option (a) is the correct answer.

39.  Which of the following is correct?

1. $\sin 1^\circ  > \sin 1$ 

2. $\sin 1^\circ  < \sin 1$ 

3. $\sin 1^\circ  = \sin 1$ 

4. $\sin 1^\circ  = \dfrac{\pi }{{18^\circ }}\sin 1$ 

Ans: We know that when $\theta $ increases, the value of $\sin \theta $ also increases.

Therefore, $\sin 1^\circ  < \sin 1$

(Since $1radian = \dfrac{\pi }{{180}}\sin 1$ )

Hence, option (d) is the correct answer.

40.  If $\tan \alpha  = \dfrac{m}{{m + 1}}$, $\tan \beta  = \dfrac{1}{{2m + 1}}$, then $\alpha  + \beta $ is equal to

1. $\dfrac{\pi }{2}$ 

2. $\dfrac{\pi }{3}$ 

3. $\dfrac{\pi }{6}$ 

4. $\dfrac{\pi }{4}$ 

Ans: We have, $\tan \alpha  = \dfrac{m}{{m + 1}}$ and $\tan \beta  = \dfrac{1}{{2m + 1}}$

We know that $\tan (A + B) = \dfrac{{\tan A + \tan B}}{{1 - \tan A.\tan B}}$. Therefore on substituting the values, we get

$ \Rightarrow \tan (\alpha  + \beta ) = \dfrac{{\dfrac{m}{{m + 1}} + \dfrac{1}{{2m + 1}}}}{{1 - \dfrac{m}{{m + 1}}.\dfrac{1}{{2m + 1}}}}$

$ \Rightarrow \tan (\alpha  + \beta ) = \dfrac{{\dfrac{{m\left( {2m + 1} \right) + m + 1}}{{\left( {m + 1} \right)\left( {2m + 1} \right)}}}}{{\dfrac{{\left( {m + 1} \right)\left( {2m + 1} \right) - m}}{{\left( {m + 1} \right)\left( {2m + 1} \right)}}}}$

On canceling common terms, we get

$ \Rightarrow \tan (\alpha  + \beta ) = \dfrac{{2{m^2} + m + m + 1}}{{2{m^2} + m + 2m + 1 - m}}$

On simplification, we get

$ \Rightarrow \tan (\alpha  + \beta ) = \dfrac{{2{m^2} + 2m + 1}}{{2{m^2} + 2m + 1}} = 1$

We know that $\tan \dfrac{\pi }{4} = 1$. Therefore, we get

$ \Rightarrow \tan (\alpha  + \beta ) = \tan \dfrac{\pi }{4}$

$ \Rightarrow \alpha  + \beta  = \dfrac{\pi }{4}$

Hence, option (d) is the correct answer.

41.  The minimum value of $3\cos x + 4\sin x + 8$ is

1. $5$ 

2. $9$ 

3. $7$ 

4. $3$ 

Ans: Given expression, $3\cos x + 4\sin x + 8$

Let $y = 3\cos x + 4\sin x + 8$ 

Transport $8$ to the LHS

$ \Rightarrow y - 8 = 3\cos x + 4\sin x......\left( i \right)$

Now, we will find the minimum value of $y - 8$.

\[ \Rightarrow y - 8 =  - \sqrt {{3^2} + {4^2}} \]

\[ \Rightarrow y - 8 =  - \sqrt {9 + 16} \]

\[ \Rightarrow y - 8 =  - \sqrt {25} \]

\[ \Rightarrow y - 8 =  - 5\]

Now, we will find the minimum value of $3\cos x + 4\sin x + 8$.

\[ \Rightarrow y =  - 5 + 8\]

\[ \Rightarrow y = 3\]

Therefore, the minimum value of $3\cos x + 4\sin x + 8$ is $3$.

Hence, option (d) is the correct answer.

42.  The value of $\tan 3A - \tan 2A - \tan A$ is equal to

1. $\tan 3A\tan 2A\tan A$ 

2. $ - \tan 3A\tan 2A\tan A$ 

3. $\tan A\tan 2A - \tan 2A\tan 3A - \tan 3A\tan A$ 

4. None of these

Ans: Given expression, $\tan 3A - \tan 2A - \tan A$

We can write $\tan 3A = \tan \left( {2A + A} \right)$.

We know that $\tan \left( {x + y} \right) = \dfrac{{\tan x + \tan y}}{{1 - \tan x\tan y}}$. Therefore, we get

$ \Rightarrow \tan 3A = \dfrac{{\tan 2A + \tan A}}{{1 - \tan 2A\tan A}}$

Now, we will cross multiply the above written equation.

$ \Rightarrow \tan 3A\left( {1 - \tan 2A\tan A} \right) = \tan 2A + \tan A$

On multiplication of terms, we get

$ \Rightarrow \tan 3A - \tan 3A\tan 2A\tan A = \tan 2A + \tan A$

$ \Rightarrow \tan 3A - \tan 2A - \tan A = \tan 3A\tan 2A\tan A$

Hence, option (a) is the correct answer.

43.  The value of $\sin \left( {45^\circ  + \theta } \right) - \cos \left( {45^\circ  - \theta } \right)$ is

1. $2\cos \theta $ 

2. $2\sin \theta $ 

3. $1$ 

4. $0$ 

Ans: Given, $\sin \left( {45^\circ  + \theta } \right) - \cos \left( {45^\circ  - \theta } \right)$

As we know $\sin \left( {A + B} \right) = \sin A\cos B + \cos A\sin B$ and $\cos \left( {A - B} \right) = \cos A\cos B + \sin A\sin B$. Therefore, we get

$ \Rightarrow \left( {\sin 45^\circ \cos \theta  + \cos 45^\circ \sin \theta } \right) - \left( {\cos 45^\circ \cos \theta  + \sin 45^\circ \sin \theta } \right)$

Substitute value of $\sin 45^\circ  = \dfrac{1}{{\sqrt 2 }}$ and $\cos 45^\circ  = \dfrac{1}{{\sqrt 2 }}$.

$ \Rightarrow \left( {\dfrac{1}{{\sqrt 2 }}\cos \theta  + \dfrac{1}{{\sqrt 2 }}\sin \theta } \right) - \left( {\dfrac{1}{{\sqrt 2 }}\cos \theta  + \dfrac{1}{{\sqrt 2 }}\sin \theta } \right)$

$ \Rightarrow \dfrac{1}{{\sqrt 2 }}\cos \theta  + \dfrac{1}{{\sqrt 2 }}\sin \theta  - \dfrac{1}{{\sqrt 2 }}\cos \theta  - \dfrac{1}{{\sqrt 2 }}\sin \theta $

$ \Rightarrow 0$ 

Hence, option (d) is the correct answer.

44.  The value of $\cot \left( {\dfrac{\pi }{4} + \theta } \right)\cot \left( {\dfrac{\pi }{4} - \theta } \right)$ is

1. $ - 1$ 

2. $0$ 

3. $1$ 

4. Not defined

Ans: We have, $\cot \left( {\dfrac{\pi }{4} + \theta } \right)\cot \left( {\dfrac{\pi }{4} - \theta } \right)$

We know that $\cot \left( {x + y} \right) = \dfrac{{\cot x.\cot y - 1}}{{\cot y + \cot x}}$ and $\cot \left( {x - y} \right) = \dfrac{{\cot x.\cot y + 1}}{{\cot y - \cot x}}$. Therefore, we get

$ \Rightarrow \dfrac{{\cot \dfrac{\pi }{4}.\cot \theta  - 1}}{{\cot \theta  + \cot \dfrac{\pi }{4}}} \times \dfrac{{\cot \dfrac{\pi }{4}.\cot \theta  + 1}}{{\cot \theta  - \cot \dfrac{\pi }{4}}}$

Substitute value of $\cos \dfrac{\pi }{4} = 1$.

$ \Rightarrow \dfrac{{1.\cot \theta  - 1}}{{\cot \theta  + 1}} \times \dfrac{{1.\cot \theta  + 1}}{{\cot \theta  - 1}}$

$ \Rightarrow \dfrac{{\cot \theta  - 1}}{{\cot \theta  + 1}} \times \dfrac{{\cot \theta  + 1}}{{\cot \theta  - 1}}$

On canceling common terms, we get

$ \Rightarrow 1$ 

Hence, option (c) is the correct answer.

45. $\cos 2\theta \cos 2\phi  + {\sin ^2}\left( {\theta  - \phi } \right) - {\sin ^2}\left( {\theta  + \phi } \right)$ is equal to

1. $\sin 2\left( {\theta  + \phi } \right)$ 

2. $\cos 2\left( {\theta  + \phi } \right)$ 

3. $\sin 2\left( {\theta  - \phi } \right)$ 

4. $\cos 2\left( {\theta  - \phi } \right)$ 

Ans: We have, $\cos 2\theta \cos 2\phi  + {\sin ^2}\left( {\theta  - \phi } \right) - {\sin ^2}\left( {\theta  + \phi } \right)$

We know that ${\sin ^2}A - {\sin ^2}B = \sin \left( {A + B} \right).\sin \left( {A - B} \right)$. Therefore, we get

$ \Rightarrow \cos 2\theta \cos 2\phi  + \sin \left( {\theta  - \phi  + \theta  + \phi } \right).\sin \left( {\theta  - \phi  - \theta  - \phi } \right)$

$ \Rightarrow \cos 2\theta \cos 2\phi  + \sin \left( {2\theta } \right).\sin \left( { - 2\phi } \right)$

We know that $\sin \left( { - \theta } \right) =  - \sin \theta $. Therefore, we get

$ \Rightarrow \cos 2\theta \cos 2\phi  - \sin 2\theta \sin 2\phi $

We know that $\cos \left( {A + B} \right) = \cos A\cos B - \sin A\sin B$. Therefore, we get

$ \Rightarrow \cos 2\left( {\theta  + \phi } \right)$

Hence, option (b) is the correct answer.

46.  The value of $\cos 12^\circ  + \cos 84^\circ  + \cos 156^\circ  + \cos 132^\circ $ is

1. $\dfrac{1}{2}$ 

2. $1$ 

3. $ - \dfrac{1}{2}$ 

4. $\dfrac{1}{8}$ 

Ans: Given expression: $\cos 12^\circ  + \cos 84^\circ  + \cos 156^\circ  + \cos 132^\circ $

$ \Rightarrow \left( {\cos 132^\circ  + \cos 12^\circ } \right) + \left( {\cos 156^\circ  + \cos 84^\circ } \right)$

We know that $\cos A + \cos B = 2\cos \dfrac{{A + B}}{2}\cos \dfrac{{A - B}}{2}$. Therefore, we get

$ \Rightarrow 2\cos \left( {\dfrac{{132^\circ  + 12^\circ }}{2}} \right).\cos \left( {\dfrac{{132^\circ  - 12^\circ }}{2}} \right) + 2\cos \left( {\dfrac{{156^\circ  + 84^\circ }}{2}} \right).\cos \left( {\dfrac{{156^\circ  - 84^\circ }}{2}} \right)$

$ \Rightarrow 2\cos \left( {\dfrac{{144^\circ }}{2}} \right).\cos \left( {\dfrac{{120^\circ }}{2}} \right) + 2\cos \left( {\dfrac{{240^\circ }}{2}} \right).\cos \left( {\dfrac{{72^\circ }}{2}} \right)$

$ \Rightarrow 2\cos \left( {72^\circ } \right).\cos \left( {60^\circ } \right) + 2\cos \left( {120^\circ } \right).\cos \left( {36^\circ } \right)$

Substitute value of $\cos 60^\circ  = \dfrac{1}{2}$ and $\cos 120^\circ  =  - \dfrac{1}{2}$.

$ \Rightarrow 2\cos \left( {72^\circ } \right) \times \dfrac{1}{2} \times  + 2 \times  - \dfrac{1}{2} \times \cos \left( {36^\circ } \right)$

$ \Rightarrow \cos 72^\circ  - \cos 36^\circ $

$ \Rightarrow \cos \left( {90^\circ  - 18^\circ } \right) - \cos 36^\circ $

We know that $\cos \left( {90^\circ  - \theta } \right) = \sin \theta $. Therefore, we get

$ \Rightarrow \sin 18^\circ  - \cos 36^\circ $

Substitute value of $\sin 18^\circ  = \dfrac{{\sqrt 5  - 1}}{4}$ and $\cos 36^\circ  = \dfrac{{\sqrt 5  + 1}}{4}$.

$ \Rightarrow \dfrac{{\sqrt 5  - 1}}{4} - \dfrac{{\sqrt 5  + 1}}{4}$

$ \Rightarrow \dfrac{{\sqrt 5  - 1 - \sqrt 5  - 1}}{4}$

$ \Rightarrow \dfrac{{ - 2}}{4}$

$ \Rightarrow \dfrac{{ - 1}}{2}$

Hence, option (c) is the correct answer.

47.  If $\tan A = \dfrac{1}{2}$, $\tan B = \dfrac{1}{3}$, then $\tan \left( {2A + B} \right)$ is equal to

1. $1$ 

2. $2$ 

3. $3$ 

4. $4$ 

Ans: Given, $\tan A = \dfrac{1}{2}$, $\tan B = \dfrac{1}{3}$

We know that $\tan 2x = \dfrac{{2\tan x}}{{1 - {{\tan }^2}x}}$. Therefore, we get

$ \Rightarrow \tan 2A = \dfrac{{2\tan A}}{{1 - {{\tan }^2}A}}$

Now, we will substitute the value of $\tan A = \dfrac{1}{2}$

$ \Rightarrow \tan 2A = \dfrac{{2 \times \dfrac{1}{2}}}{{1 - \dfrac{{{1^2}}}{{{2^2}}}}}$

$ \Rightarrow \tan 2A = \dfrac{1}{{\dfrac{{4 - 1}}{4}}} = \dfrac{1}{{\dfrac{3}{4}}}$

$ \Rightarrow \tan 2A = \dfrac{4}{3}$

We need to find value of $\tan \left( {2A + B} \right)$

We know that $\tan \left( {x + y} \right) = \dfrac{{\tan x + \tan y}}{{1 - \tan x.\tan y}}$. Therefore, we get

$ \Rightarrow \tan \left( {2A + B} \right) = \dfrac{{\tan 2A + \tan B}}{{1 - \tan 2A.\tan B}}$

$ \Rightarrow \tan \left( {2A + B} \right) = \dfrac{{\dfrac{4}{3} + \dfrac{1}{3}}}{{1 - \dfrac{4}{3}.\dfrac{1}{3}}}$

$ \Rightarrow \tan \left( {2A + B} \right) = \dfrac{{\dfrac{5}{3}}}{{\dfrac{{9 - 4}}{9}}}$

$ \Rightarrow \tan \left( {2A + B} \right) = \dfrac{5}{3} \times \dfrac{9}{5}$

$ \Rightarrow \tan \left( {2A + B} \right) = 3$

Hence, option (c) is the correct answer.

48.  The value of $\sin \dfrac{\pi }{{10}}\sin \dfrac{{13\pi }}{{10}}$ is 

1. $\dfrac{1}{2}$ 

2. $ - \dfrac{1}{2}$ 

3. $ - \dfrac{1}{4}$ 

4. $1$ 

Ans: We have, $\sin \dfrac{\pi }{{10}}\sin \dfrac{{13\pi }}{{10}}$

$ \Rightarrow \sin \dfrac{\pi }{{10}}\sin \left( {\pi  + \dfrac{{3\pi }}{{10}}} \right)$ 

We know that $\sin \left( {\pi  + \theta } \right) =  - \sin \theta $. Therefore, we get

$ \Rightarrow \sin \dfrac{\pi }{{10}}\sin \left( { - \dfrac{{3\pi }}{{10}}} \right)$

We know that $\sin \left( { - \theta } \right) =  - \sin \theta $. Therefore, we get

$ \Rightarrow  - \sin \dfrac{{180^\circ }}{{10}}\sin \left( {\dfrac{{3 \times 180^\circ }}{{10}}} \right)$

$ \Rightarrow  - \sin 18^\circ .\sin 54^\circ $

$ \Rightarrow  - \sin 18^\circ .\sin \left( {90^\circ  - 36^\circ } \right)$

We know that $\sin \left( {90^\circ  - \theta } \right) = \cos \theta $. Therefore, we get

$ \Rightarrow  - \sin 18^\circ .\cos 36^\circ $

On substituting the values $\sin 18^\circ  = \dfrac{{\sqrt 5  - 1}}{4}$ and $\cos 36^\circ  = \dfrac{{\sqrt 5  + 1}}{4}$, we get

$ \Rightarrow  - \left( {\dfrac{{\sqrt 5  - 1}}{4}} \right)\left( {\dfrac{{\sqrt 5  + 1}}{4}} \right)$

$ \Rightarrow  - \left( {\dfrac{{5 - 1}}{{16}}} \right)$

$ \Rightarrow  - \left( {\dfrac{4}{{16}}} \right) =  - \dfrac{1}{4}$

Hence, option (c) is the correct answer.

49.  The value of $\sin 50^\circ  - \sin 70^\circ  + \sin 10^\circ $ is equal to

1. $1$ 

2. $0$ 

3. $\dfrac{1}{2}$ 

4. $2$ 

Ans: Given expression, $\sin 50^\circ  - \sin 70^\circ  + \sin 10^\circ $

$ \Rightarrow \left( {\sin 50^\circ  - \sin 70^\circ } \right) + \sin 10^\circ $

We know that $\sin C - \sin D = 2\cos \dfrac{{C + D}}{2}\sin \dfrac{{C - D}}{2}$. Therefore, we get

$ \Rightarrow 2\cos \dfrac{{50^\circ  + 70^\circ }}{2}\sin \dfrac{{50^\circ  - 70^\circ }}{2} + \sin 10^\circ $

$ \Rightarrow 2\cos 60^\circ \sin \left( { - 10^\circ } \right) + \sin 10^\circ $

We know that $\sin \left( { - \theta } \right) =  - \sin \theta $. Therefore, we get

$ \Rightarrow  - 2\cos 60^\circ \sin 10^\circ  + \sin 10^\circ $

Substitute value of $\sin 60^\circ  = \dfrac{1}{2}$.

$ \Rightarrow  - 2 \times \dfrac{1}{2} \times \sin 10^\circ  + \sin 10^\circ $

$ \Rightarrow  - \sin 10^\circ  + \sin 10^\circ $

$ \Rightarrow 0$

Hence, option (b) is the correct answer.

50.  If $\sin \theta  + \cos \theta  = 1$, then the value of $\sin 2\theta $ is equal to

1. $1$ 

2. $\dfrac{1}{2}$ 

3. $0$ 

4. $ - 1$ 

Ans: Given, $\sin \theta  + \cos \theta  = 1$

On squaring both the sides, we get

$ \Rightarrow {\left( {\sin \theta  + \cos \theta } \right)^2} = {1^2}$

As we know ${\left( {a + b} \right)^2} = {a^2} + {b^2} + 2ab$. So, on applying this identity, we get

$ \Rightarrow {\sin ^2}\theta  + {\cos ^2}\theta  + 2\sin \theta \cos \theta  = 1$

As we know ${\sin ^2}\theta  + {\cos ^2}\theta  = 1$. So, on applying this formula, we get

\[ \Rightarrow 1 + 2\sin \theta \cos \theta  = 1\]

As we know $\sin 2A = 2\sin A\cos A$. Therefore, we get

\[ \Rightarrow 2\sin \theta \cos \theta  = 1 - 1\]

\[ \Rightarrow \sin 2\theta  = 0\]

Hence, option (c) is the correct answer.

51.  If $\alpha  + \beta  = \dfrac{\pi }{4}$, then the value of $\left( {1 + \tan \alpha } \right)\left( {1 + \tan \beta } \right)$ is 

1. $1$ 

2. $2$ 

3. $ - 2$ 

4. Not defined

Ans: Given, $\alpha  + \beta  = \dfrac{\pi }{4}$

$ \Rightarrow \tan \left( {\alpha  + \beta } \right) = \tan \dfrac{\pi }{4}$

We know that $\tan \left( {x + y} \right) = \dfrac{{\tan x + \tan y}}{{1 - \tan x\tan y}}$. Therefore, we get

$ \Rightarrow \dfrac{{\tan \alpha  + \tan \beta }}{{1 - \tan \alpha \tan \beta }} = \tan \dfrac{\pi }{4}$

On substituting the value of $\tan \dfrac{\pi }{4} = 1$, we get

$ \Rightarrow \dfrac{{\tan \alpha  + \tan \beta }}{{1 - \tan \alpha \tan \beta }} = 1$

On cross-multiplication, we get

$ \Rightarrow \tan \alpha  + \tan \beta  = 1 - \tan \alpha \tan \beta $

$ \Rightarrow \tan \alpha  + \tan \beta  + \tan \alpha \tan \beta  = 1$

Add $1$ to both the sides

$ \Rightarrow 1 + \tan \alpha  + \tan \beta  + \tan \alpha \tan \beta  = 1 + 1$

Take $\tan \beta $ as a common term.

$ \Rightarrow \left( {1 + \tan \alpha } \right) + \tan \beta \left( {1 + \tan \alpha } \right) = 2$

$ \Rightarrow \left( {1 + \tan \alpha } \right)\left( {1 + \tan \alpha } \right) = 2$

Hence, option (b) is the correct answer.

52.  If $\sin \theta  = \dfrac{{ - 4}}{5}$ and $\theta $ lies in third quadrant then the value of \[\cos \dfrac{\theta }{2}\] is

1. $\dfrac{1}{5}$ 

2. $ - \dfrac{1}{{\sqrt {10} }}$ 

3. $ - \dfrac{1}{{\sqrt 5 }}$ 

4. $\dfrac{1}{{\sqrt {10} }}$ 

Ans: Given, $\sin \theta  = \dfrac{{ - 4}}{5}$. Here, value of $\sin e$ is negative because $\theta $ lies in third quadrant. As here we need to find \[\cos \dfrac{\theta }{2}\], so we will first find the value of $\cos \theta $.

We know that ${\sin ^2}\theta  + {\cos ^2}\theta  = 1$. 

$ \Rightarrow \cos \theta  = \sqrt {1 - {{\sin }^2}\theta } $ 

Substitute the value of $\sin \theta  = \dfrac{{ - 4}}{5}$.

$ \Rightarrow \cos \theta  = \sqrt {1 - {{\left( {\dfrac{{ - 4}}{5}} \right)}^2}} $

\[ \Rightarrow \cos \theta  = \sqrt {1 - \dfrac{{16}}{{25}}} \]

On taking LCM, we get

\[ \Rightarrow \cos \theta  = \sqrt {\dfrac{{25 - 16}}{{25}}} \]

\[ \Rightarrow \cos \theta  = \sqrt {\dfrac{9}{{25}}} \]

\[ \Rightarrow \cos \theta  =  \pm \dfrac{3}{5}\]

As it is mentioned in the question that $\theta $ lies in the third quadrant and we know $\cos $ is negative in the third quadrant. Therefore, we get

\[ \Rightarrow \cos \theta  =  - \dfrac{3}{5}\]

We know that $\cos \theta  = 2{\cos ^2}\dfrac{\theta }{2} - 1$. Now we will substitute value of $\cos \theta $ in this identity.

$ \Rightarrow \dfrac{{ - 3}}{5} = 2{\cos ^2}\dfrac{\theta }{2} - 1$

(Here, value of $\cos \theta $ is negative because $\pi  < \theta  < \dfrac{{3\pi }}{2}$ )

$ \Rightarrow 2{\cos ^2}\dfrac{\theta }{2} = 1 - \dfrac{3}{5}$

$ \Rightarrow 2{\cos ^2}\dfrac{\theta }{2} = \dfrac{2}{5}$

On canceling common term, we get

$ \Rightarrow {\cos ^2}\dfrac{\theta }{2} = \dfrac{1}{5}$

$ \Rightarrow \cos \dfrac{\theta }{2} =  \pm \dfrac{1}{{\sqrt 5 }}$

As we know $\pi  < \theta  < \dfrac{{3\pi }}{2}$. Therefore, $\dfrac{\pi }{2} < \dfrac{\theta }{2} < \dfrac{{3\pi }}{4}$ 

$ \Rightarrow \cos \dfrac{\theta }{2} =  - \dfrac{1}{{\sqrt 5 }}$

Hence, option (c) is the correct answer.

53.  Number of solutions of the equation $\tan x + \sec x = 2\cos x$ lying in the interval $\left[ {0,2\pi } \right]$ is

1. $0$ 

2. $1$ 

3. $2$ 

4. $3$ 

Ans: Given that, $\tan x + \sec x = 2\cos x$

We will first write above written equation in terms of $\sin e$ and $\cos $.

$ \Rightarrow \dfrac{{\sin x}}{{\cos x}} + \dfrac{1}{{\cos x}} = 2\cos x$ 

$ \Rightarrow \dfrac{{\sin x + 1}}{{\cos x}} = 2\cos x$

$ \Rightarrow \sin x + 1 = 2{\cos ^2}x$

$ \Rightarrow 2{\cos ^2}x - \sin x - 1 = 0$

$ \Rightarrow 2\left( {1 - {{\sin }^2}x} \right) - \sin x - 1 = 0$

$ \Rightarrow  - 2{\sin ^2}x - \sin x + 1 = 0$

$ \Rightarrow 2{\sin ^2}x + \sin x - 1 = 0$

Since, the above written equation is a quadratic equation in $\sin x$. Therefore, it will have $2$ solutions.

Hence, option (c) is the correct answer.

54.  The value of $\sin \dfrac{\pi }{{18}} + \sin \dfrac{\pi }{9} + \sin \dfrac{{2\pi }}{9} + \sin \dfrac{{5\pi }}{{18}}$ is given by

1. $\sin \dfrac{{7\pi }}{{18}} + \sin \dfrac{{4\pi }}{9}$ 

2. $1$ 

3. $\cos \dfrac{\pi }{6} + \cos \dfrac{{3\pi }}{7}$ 

4. $\cos \dfrac{\pi }{9} + \sin \dfrac{\pi }{9}$ 

Ans: Given expression: $\sin \dfrac{\pi }{{18}} + \sin \dfrac{\pi }{9} + \sin \dfrac{{2\pi }}{9} + \sin \dfrac{{5\pi }}{{18}}$

$ \Rightarrow \left( {\sin \dfrac{{5\pi }}{{18}} + \sin \dfrac{\pi }{{18}}} \right) + \left( {\sin \dfrac{{2\pi }}{9} + \sin \dfrac{\pi }{9}} \right)$

We know that $\sin A + \sin B = 2\sin \dfrac{{A + B}}{2}\cos \dfrac{{A - B}}{2}$. Therefore, we get

$ \Rightarrow 2\sin \left( {\dfrac{{\dfrac{{5\pi }}{{18}} + \dfrac{\pi }{{18}}}}{2}} \right).\cos \left( {\dfrac{{\dfrac{{5\pi }}{{18}} - \dfrac{\pi }{{18}}}}{2}} \right) + 2\sin \left( {\dfrac{{\dfrac{{2\pi }}{9} + \dfrac{\pi }{9}}}{2}} \right).\cos \left( {\dfrac{{\dfrac{{2\pi }}{9} - \dfrac{\pi }{9}}}{2}} \right)$

$ \Rightarrow 2\sin \left( {\dfrac{{\dfrac{{6\pi }}{{18}}}}{2}} \right).\cos \left( {\dfrac{{\dfrac{{4\pi }}{{18}}}}{2}} \right) + 2\sin \left( {\dfrac{{\dfrac{{3\pi }}{9}}}{2}} \right).\cos \left( {\dfrac{{\dfrac{\pi }{9}}}{2}} \right)$

$ \Rightarrow 2\sin \left( {\dfrac{\pi }{6}} \right).\cos \left( {\dfrac{\pi }{9}} \right) + 2\sin \left( {\dfrac{\pi }{6}} \right).\cos \left( {\dfrac{\pi }{{18}}} \right)$

Substitute value of $\sin \dfrac{\pi }{6} = \dfrac{1}{2}$.

$ \Rightarrow 2 \times \dfrac{1}{2} \times \cos \left( {\dfrac{\pi }{9}} \right) + 2 \times \dfrac{1}{2} \times \cos \left( {\dfrac{\pi }{{18}}} \right)$

$ \Rightarrow \cos \left( {\dfrac{\pi }{9}} \right) + \cos \left( {\dfrac{\pi }{{18}}} \right)$

We know that $\cos \theta  = \sin \left( {90^\circ  - \theta } \right)$. Therefore, we get

$ \Rightarrow \sin \left( {\dfrac{\pi }{2} - \dfrac{\pi }{9}} \right) + \sin \left( {\dfrac{\pi }{2} - \dfrac{\pi }{{18}}} \right)$

$ \Rightarrow \sin \dfrac{{7\pi }}{{18}} + \sin \dfrac{{8\pi }}{{18}}$

$ \Rightarrow \sin \dfrac{{7\pi }}{{18}} + \sin \dfrac{{4\pi }}{9}$

Hence, option (a) is the correct answer.

55.  If $A$ lies in the second quadrant and $3\tan A + 4 = 0$, then the value of $2\cot A - 5\cos A + \sin A$ is equal to

1. $\dfrac{{ - 53}}{{10}}$ 

2. $\dfrac{{23}}{{10}}$ 

3. $\dfrac{{37}}{{10}}$ 

4. $\dfrac{7}{{10}}$ 

Ans: Given, $3\tan A + 4 = 0$

$ \Rightarrow 3\tan A =  - 4$

$ \Rightarrow \tan A = \dfrac{{ - 4}}{3} = \dfrac{P}{B}$

We know that ${H^2} = {P^2} + {B^2}$ 

$ \Rightarrow {H^2} = {\left( { - 4} \right)^2} + {\left( 3 \right)^2}$

$ \Rightarrow {H^2} = 16 + 9$

$ \Rightarrow {H^2} = 25$

$ \Rightarrow H = 5$

We know that $\cos x = \dfrac{B}{H}$. Therefore, we get

$ \Rightarrow \cos A = \dfrac{{ - 3}}{5}$ (Negative because $A$ lies in second quadrant)

We know that $\sin x = \dfrac{P}{H}$. Therefore, we get

$ \Rightarrow \sin A = \dfrac{4}{5}$

We know that $\cot x = \dfrac{B}{P}$. Therefore, we get

$ \Rightarrow \cot A = \dfrac{{ - 3}}{4}$ (Negative because $A$ lies in second quadrant)

We need to find the value of $2\cot A - 5\cos A + \sin A$

$ \Rightarrow 2 \times \dfrac{{ - 3}}{4} - 5 \times \left( {\dfrac{{ - 3}}{5}} \right) + \dfrac{4}{5}$

$ \Rightarrow \dfrac{{ - 3}}{2} + 3 + \dfrac{4}{5}$

$ \Rightarrow \dfrac{{ - 15 + 30 + 8}}{{10}}$

$ \Rightarrow \dfrac{{23}}{{10}}$

Hence, option (a) is the correct answer.

56.  The value of ${\cos ^2}48^\circ  - {\sin ^2}12^\circ $ is

1. $\dfrac{{\sqrt 5  + 1}}{8}$ 

2. $\dfrac{{\sqrt 5  - 1}}{8}$ 

3. $\dfrac{{\sqrt 5  + 1}}{5}$ 

4. $\dfrac{{\sqrt 5  + 1}}{{2\sqrt 2 }}$ 

Ans: Given expression: ${\cos ^2}48^\circ  - {\sin ^2}12^\circ $

We know that ${\cos ^2}A - {\sin ^2}A = \cos \left( {A + B} \right).\cos \left( {A - B} \right)$. Therefore, we get

$ \Rightarrow \cos \left( {48^\circ  + 12^\circ } \right).\cos \left( {48^\circ  - 12^\circ } \right)$

$ \Rightarrow \cos 60^\circ .\cos 36^\circ $

On substituting the values, $\cos 60^\circ  = \dfrac{1}{2}$ and $\cos 36^\circ  = \dfrac{{\sqrt 5  + 1}}{4}$. Therefore, we get

$ \Rightarrow \dfrac{1}{2} \times \dfrac{{\sqrt 5  + 1}}{4}$

$ \Rightarrow \dfrac{{\sqrt 5  + 1}}{8}$

Hence, option (a) is the correct answer.

57.  If $\tan \alpha  = \dfrac{1}{7}$, $\tan \beta  = \dfrac{1}{3}$, then $\cos 2\alpha $ is equal to

1. $\sin 2\beta $ 

2. $\sin 4\beta $ 

3. $\sin 3\beta $ 

4. $\cos 2\beta $ 

Ans: Given, $\tan \alpha  = \dfrac{1}{7}$, $\tan \beta  = \dfrac{1}{3}$

We know that $\cos 2x = \dfrac{{1 - {{\tan }^2}x}}{{1 + {{\tan }^2}x}}$. Therefore, we get

$ \Rightarrow \cos 2\alpha  = \dfrac{{1 - {{\tan }^2}\alpha }}{{1 + {{\tan }^2}\alpha }} = \dfrac{{1 - \dfrac{{{1^2}}}{{{7^2}}}}}{{1 + \dfrac{{{1^2}}}{{{7^2}}}}}$

$ \Rightarrow \cos 2\alpha  = \dfrac{{\dfrac{{{7^2} - 1}}{{{7^2}}}}}{{\dfrac{{{7^2} + 1}}{{{7^2}}}}} = \dfrac{{{7^2} - 1}}{{{7^2} + 1}}$

$ \Rightarrow \cos 2\alpha  = \dfrac{{49 - 1}}{{49 + 1}} = \dfrac{{48}}{{50}}$

$ \Rightarrow \cos 2\alpha  = \dfrac{{24}}{{25}}$

Similarly, 

$ \Rightarrow \tan 2\beta  = \dfrac{{2\tan \beta }}{{1 - {{\tan }^2}\beta }}$

$ \Rightarrow \tan 2\beta  = \dfrac{{2 \times \dfrac{1}{3}}}{{1 - \dfrac{{{1^2}}}{{{3^2}}}}}$

$ \Rightarrow \tan 2\beta  = \dfrac{{\dfrac{2}{3}}}{{\dfrac{8}{9}}} = \dfrac{2}{3} \times \dfrac{9}{8}$

$ \Rightarrow \tan 2\beta  = \dfrac{3}{4}$

We know that $\sin 2x = \dfrac{{2\tan x}}{{1 + {{\tan }^2}x}}$. Therefore, we get

$ \Rightarrow \sin 4\beta  = \dfrac{{2\tan 2\beta }}{{1 + {{\tan }^2}2\beta }}$

$ \Rightarrow \sin 4\beta  = \dfrac{{2 \times \dfrac{3}{4}}}{{1 + \dfrac{{{3^2}}}{{{4^2}}}}}$

$ \Rightarrow \sin 4\beta  = \dfrac{{\dfrac{6}{4}}}{{\dfrac{{16 + 9}}{{16}}}}$

$ \Rightarrow \sin 4\beta  = \dfrac{6}{4} \times \dfrac{{16}}{{25}}$

$ \Rightarrow \sin 4\beta  = \dfrac{{24}}{{25}} = \cos 2\alpha $

Hence, option (b) is the correct answer.

58.  If $\tan \theta  = \dfrac{a}{b}$, then $b\cos 2\theta  + a\sin 2\theta $ is equal to

1. $a$ 

2. $b$ 

3. $\dfrac{a}{b}$ 

4. None

Ans: Given, $\tan \theta  = \dfrac{a}{b}$

We have, $b\cos 2\theta  + a\sin 2\theta $

We know that $\cos 2x = \dfrac{{1 - {{\tan }^2}x}}{{1 + {{\tan }^2}x}}$ and $\sin 2x = \dfrac{{2\tan x}}{{1 + {{\tan }^2}x}}$. Therefore, we get

$ \Rightarrow b\left[ {\dfrac{{1 - {{\tan }^2}\theta }}{{1 + {{\tan }^2}\theta }}} \right] + a\left[ {\dfrac{{2\tan \theta }}{{1 + {{\tan }^2}\theta }}} \right]$

Substitute $\tan \theta  = \dfrac{a}{b}$

$ \Rightarrow b\left[ {\dfrac{{1 - \dfrac{{{a^2}}}{{{b^2}}}}}{{1 + \dfrac{{{a^2}}}{{{b^2}}}}}} \right] + a\left[ {\dfrac{{2\dfrac{a}{b}}}{{1 + \dfrac{{{a^2}}}{{{b^2}}}}}} \right]$

$ \Rightarrow b\left[ {\dfrac{{\dfrac{{{b^2} - {a^2}}}{{{b^2}}}}}{{\dfrac{{{b^2} + {a^2}}}{{{b^2}}}}}} \right] + a\left[ {\dfrac{{2\dfrac{a}{b}}}{{\dfrac{{{b^2} + {a^2}}}{{{b^2}}}}}} \right]$

$ \Rightarrow b\left[ {\dfrac{{{b^2} - {a^2}}}{{{b^2} + {a^2}}}} \right] + a\left[ {\dfrac{{2ab}}{{{b^2} + {a^2}}}} \right]$

$ \Rightarrow \left[ {\dfrac{{{b^3} - {a^2}b}}{{{b^2} + {a^2}}}} \right] + \left[ {\dfrac{{2{a^2}b}}{{{b^2} + {a^2}}}} \right]$

$ \Rightarrow \dfrac{{{b^3} - {a^2}b + 2{a^2}b}}{{{b^2} + {a^2}}}$

$ \Rightarrow \dfrac{{b\left( {{b^2} + {a^2}} \right)}}{{{b^2} + {a^2}}}$

$ \Rightarrow b$

Hence, option (b) is the correct answer.

59.  If for real values of $x$, $\cos \theta  = x + \dfrac{1}{x}$, then

1. $\theta $ is an acute angle

2. $\theta $ is right angle

3. $\theta $ is an obtuse angle

4. No value of $\theta $ is possible

Ans: Given, $\cos \theta  = x + \dfrac{1}{x}$

$ \Rightarrow \cos \theta  = \dfrac{{{x^2} + 1}}{x}$

$ \Rightarrow {x^2} + 1 = x\cos \theta $

$ \Rightarrow {x^2} - x\cos \theta  + 1 = 0$

We know that for real value of $x$, ${b^2} - 4ac \geqslant 0$. Therefore, we get

$ \Rightarrow {\left( { - \cos \theta } \right)^2} - 4 \times 1 \times 1 \geqslant 0$ 

$ \Rightarrow {\left( { - \cos \theta } \right)^2} - 4 \geqslant 0$

$ \Rightarrow {\cos ^2}\theta  \geqslant 4$

$ \Rightarrow \cos \theta  \geqslant  \pm 2$

We know that $ - 1 \leqslant \cos \theta  \leqslant 1$. Therefore, value of $\theta $ is not possible

Hence, option (d) is the correct answer.

Fill in the blanks in exercises $60$ to $67$.

60.  The value of $\dfrac{{\sin 50^\circ }}{{\sin 130^\circ }}$ is …….

Ans: We need to find the value of $\dfrac{{\sin 50^\circ }}{{\sin 130^\circ }}$

As we know $\sin \left( {180^\circ  - \theta } \right) = \sin \theta $. Therefore, we get

$ \Rightarrow \dfrac{{\sin 50^\circ }}{{\sin \left( {180^\circ  - 50^\circ } \right)}}$

$ \Rightarrow \dfrac{{\sin 50^\circ }}{{\sin 50^\circ }}$

On canceling the common term, we get

$ \Rightarrow 1$

Thus, value of filler is $1$.

61.  If $k = \sin \left( {\dfrac{\pi }{{18}}} \right)\sin \left( {\dfrac{{5\pi }}{{18}}} \right)\sin \left( {\dfrac{{7\pi }}{{18}}} \right)$, then the numerical value of $k$ is …….

Ans: Given, $k = \sin \left( {\dfrac{\pi }{{18}}} \right)\sin \left( {\dfrac{{5\pi }}{{18}}} \right)\sin \left( {\dfrac{{7\pi }}{{18}}} \right)$

Substitute value of $\pi  = 180^\circ $.

$ \Rightarrow k = \sin \left( {\dfrac{{180^\circ }}{{18}}} \right)\sin \left( {\dfrac{{5 \times 180^\circ }}{{18}}} \right)\sin \left( {\dfrac{{7 \times 180^\circ }}{{18}}} \right)$

On simplification, we get

$ \Rightarrow k = \sin 10^\circ .\sin 50^\circ .\sin 70^\circ $

$ \Rightarrow k = \sin 10^\circ .\sin \left( {90^\circ  - 40^\circ } \right).\sin \left( {90^\circ  - 20^\circ } \right)$

As we know $\sin \left( {90^\circ  - \theta } \right) = \cos \theta $. Therefore, we get

$ \Rightarrow k = \sin 10^\circ .\cos 40^\circ .\cos 20^\circ $

Multiply and divide above written equation by $2$ 

$ \Rightarrow k = \sin 10^\circ \dfrac{1}{2}\left[ {2\cos 40^\circ \cos 20^\circ } \right]$

We know that $2\cos x\cos y = \cos \left( {x + y} \right) + \cos \left( {x - y} \right)$. Therefore, we get

$ \Rightarrow k = \dfrac{1}{2}\sin 10^\circ \left[ {\cos \left( {40^\circ  + 20^\circ } \right) + \cos \left( {40^\circ  - 20^\circ } \right)} \right]$

$ \Rightarrow k = \dfrac{1}{2}\sin 10^\circ \left[ {\cos 60^\circ  + \cos 20^\circ } \right]$

Substitute value of $\cos 60^\circ  = \dfrac{1}{2}$.

$ \Rightarrow k = \dfrac{1}{2}\sin 10^\circ \left[ {\dfrac{1}{2} + \cos 20^\circ } \right]$

On multiplication of terms, we get

$ \Rightarrow k = \dfrac{1}{4}\sin 10^\circ  + \dfrac{1}{2}\sin 10^\circ \cos 20^\circ $

Multiply and divide $\sin 10^\circ \cos 20^\circ $ by $2$

$ \Rightarrow k = \dfrac{1}{4}\sin 10^\circ  + \dfrac{1}{2} \times \dfrac{1}{2}\left( {2\sin 10^\circ \cos 20^\circ } \right)$

We know that $2\sin x\cos y = \sin \left( {x + y} \right) + \sin \left( {x - y} \right)$. Therefore, we get

$ \Rightarrow k = \dfrac{1}{4}\sin 10^\circ  + \dfrac{1}{4}\left( {\sin \left( {10^\circ  + 20^\circ } \right) + \sin \left( {10^\circ  - 20^\circ } \right)} \right)$

$ \Rightarrow k = \dfrac{1}{4}\sin 10^\circ  + \dfrac{1}{4}\left( {\sin 30^\circ  + \sin \left( { - 10^\circ } \right)} \right)$

We know that $\sin \left( { - \theta } \right) =  - \sin \theta $ . Therefore, we get

$ \Rightarrow k = \dfrac{1}{4}\sin 10^\circ  + \dfrac{1}{4}\sin 30^\circ  - \dfrac{1}{4}\sin 10^\circ $

$ \Rightarrow k = \dfrac{1}{4}\sin 30^\circ $

Substitute the value of $\sin 30^\circ  = \dfrac{1}{2}$.

$ \Rightarrow k = \dfrac{1}{4} \times \dfrac{1}{2} = \dfrac{1}{8}$

Thus, value of filler is $\dfrac{1}{8}$.

62.  If $\tan A = \dfrac{{1 - \cos B}}{{\sin B}}$, then $\tan 2A = $ …….

Ans: Given, $\tan A = \dfrac{{1 - \cos B}}{{\sin B}}$

We know that $\tan 2A = \dfrac{{2\tan A}}{{1 - {{\tan }^2}A}}$. So, we will substitute given value of $\tan A$ in this formula.

$ \Rightarrow \tan 2A = \dfrac{{2\left( {\dfrac{{1 - \cos B}}{{\sin B}}} \right)}}{{1 - {{\left( {\dfrac{{1 - \cos B}}{{\sin B}}} \right)}^2}}}$

We know that $1 - \cos x = 2{\sin ^2}\dfrac{x}{2}$ and $\sin x = 2\sin \dfrac{x}{2}\cos \dfrac{x}{2}$. Therefore, we get

$ \Rightarrow \tan 2A = \dfrac{{2\left( {\dfrac{{2{{\sin }^2}\dfrac{B}{2}}}{{2\sin \dfrac{B}{2}\cos \dfrac{B}{2}}}} \right)}}{{1 - {{\left( {\dfrac{{2{{\sin }^2}\dfrac{B}{2}}}{{2\sin \dfrac{B}{2}\cos \dfrac{B}{2}}}} \right)}^2}}}$

$ \Rightarrow \tan 2A = \dfrac{{2\left( {\dfrac{{\sin \dfrac{B}{2}}}{{\cos \dfrac{B}{2}}}} \right)}}{{1 - {{\left( {\dfrac{{\sin \dfrac{B}{2}}}{{\cos \dfrac{B}{2}}}} \right)}^2}}}$

As we know $\dfrac{{\sin x}}{{\cos x}} = \tan x$. Therefore, we get

\[ \Rightarrow \tan 2A = \dfrac{{2\left( {\tan \dfrac{B}{2}} \right)}}{{1 - {{\tan }^2}\dfrac{B}{2}}}\]

We know that $\tan B = \dfrac{{2\tan \dfrac{B}{2}}}{{1 - {{\tan }^2}\dfrac{B}{2}}}$. Therefore, we get

\[ \Rightarrow \tan 2A = \tan B\]

Thus, value of filler is $\tan B$.

63.  If $\sin x + \cos x = a$, then

1. ${\sin ^6}x + {\cos ^6}x = $ ……

2. $\left| {\sin x - \cos x} \right| = $ ……

Ans: Given, $\sin x + \cos x = a$

On squaring both the sides, we get

$ \Rightarrow {\left( {\sin x + \cos x} \right)^2} = {a^2}$

$ \Rightarrow {\sin ^2}x + {\cos ^2}x + 2\sin x\cos x = {a^2}$

$ \Rightarrow 1 + 2\sin x\cos x = {a^2}$

$ \Rightarrow 2\sin x\cos x = {a^2} - 1$

$ \Rightarrow \sin x\cos x = \dfrac{{{a^2} - 1}}{2}.....\left( 1 \right)$

1. ${\sin ^6}x + {\cos ^6}x$ 

This can also be written as ${\left( {{{\sin }^2}x} \right)^3} + {\left( {{{\cos }^2}x} \right)^3}$.

We know that ${a^3} + {b^3} = {\left( {a + b} \right)^3} - 3ab\left( {a + b} \right)$. Therefore, we get

$ \Rightarrow {\left( {{{\sin }^2}x + {{\cos }^2}x} \right)^3} - 3{\sin ^2}x{\cos ^2}x\left( {{{\sin }^2}x + {{\cos }^2}x} \right)$ 

$ \Rightarrow 1 - 3{\sin ^2}x{\cos ^2}x$

On substituting $\sin x\cos x = \dfrac{{{a^2} - 1}}{2}$, we get

$ \Rightarrow 1 - 3{\left( {\dfrac{{{a^2} - 1}}{2}} \right)^2}$

\[ \Rightarrow 1 - \dfrac{{3{{\left( {{a^2} - 1} \right)}^2}}}{4}\]

\[ \Rightarrow \dfrac{1}{4}\left[ {4 - 3{{\left( {{a^2} - 1} \right)}^2}} \right]\]

2. $\left| {\sin x - \cos x} \right|$ 

On squaring, we get

$ \Rightarrow {\left| {\sin x - \cos x} \right|^2}$

$ \Rightarrow {\sin ^2}x + {\cos ^2}x - 2\sin x\cos x$ 

On substituting $\sin x\cos x = \dfrac{{{a^2} - 1}}{2}$, we get

$ \Rightarrow 1 - 2\left( {\dfrac{{{a^2} - 1}}{2}} \right)$

$ \Rightarrow 1 - {a^2} + 1$

$ \Rightarrow 2 - {a^2}$

$ \Rightarrow \left| {\sin x - \cos x} \right| = \sqrt {2 - {a^2}} $

We know that $\left| {\sin x - \cos x} \right| > 0$. 

Therefore, the value of filler is $\sqrt {2 - {a^2}} $.

64.  In a triangle ABC with $\angle C = 90^\circ $ the equation whose roots are $\tan A$ and $\tan B$ is ……

Ans: Given, $\vartriangle ABC$ with $\angle C = 90^\circ $

We know that quadratic equation in the form of roots is ${x^2} - \left( {\alpha  + \beta } \right)x + \alpha \beta  = 0$.

$ \Rightarrow {x^2} - \left( {\tan A + \tan B} \right)x + \tan A.\tan B = 0$ 

We know that sum of interior angle of triangle is $180^\circ $. Therefore, we get

$ \Rightarrow \angle A + \angle B + \angle C = 180^\circ $ 

$ \Rightarrow \angle A + \angle B + 90^\circ  = 180^\circ $

$ \Rightarrow \angle A + \angle B = 180^\circ $

$ \Rightarrow \tan \left( {A + B} \right) = \tan 90^\circ $ 

We know that $\tan \left( {x + y} \right) = \dfrac{{\tan x + \tan y}}{{1 - \tan x\tan y}}$. Therefore, we get

$ \Rightarrow \dfrac{{\tan A + \tan B}}{{1 - \tan A\tan B}} = \dfrac{1}{0}$

On cross multiplication, we get

$ \Rightarrow 1 - \tan A\tan B = 0$

$ \Rightarrow \tan A\tan B = 1....\left( i \right)$

Now, $\tan A + \tan B$ 

$ \Rightarrow \dfrac{{\sin A}}{{\cos A}} + \dfrac{{\sin B}}{{\cos B}}$ 

$ \Rightarrow \dfrac{{\sin A\cos B + \cos A\sin B}}{{\cos A\cos B}}$

We know that $\sin \left( {A + B} \right) = \sin A\cos B + \cos A\sin B$. Therefore, we get

$ \Rightarrow \dfrac{{\sin \left( {A + B} \right)}}{{\cos A\cos B}}$

$ \Rightarrow \dfrac{{\sin 90^\circ }}{{\cos A\cos \left( {90^\circ  - A} \right)}}$

$ \Rightarrow \dfrac{1}{{\cos A\sin A}}$

$ \Rightarrow \dfrac{2}{{2\cos A\sin A}}$

We know that $\sin 2A = 2\sin A\cos A$. Therefore, we get

$ \Rightarrow \dfrac{2}{{\sin 2A}}$

$ \Rightarrow \tan A + \tan B = \dfrac{2}{{\sin 2A}}.....\left( {ii} \right)$

We have, ${x^2} - \left( {\tan A + \tan B} \right)x + \tan A.\tan B = 0$. Therefore, from equation $\left( i \right)$ and $\left( {ii} \right)$, we get

$ \Rightarrow {x^2} - \left( {\dfrac{2}{{\sin 2A}}} \right)x + 1 = 0$

Therefore, the value of filler is ${x^2} - \left( {\dfrac{2}{{\sin 2A}}} \right)x + 1 = 0$.

65.  $3{\left( {\sin x - \cos x} \right)^4} + 6{\left( {\sin x + \cos x} \right)^2} + 4\left( {{{\sin }^6}x + {{\cos }^6}x} \right) = $ …….

Ans: Given expression: $3{\left( {\sin x - \cos x} \right)^4} + 6{\left( {\sin x + \cos x} \right)^2} + 4\left( {{{\sin }^6}x + {{\cos }^6}x} \right)$

$ \Rightarrow 3{\left[ {{{\left( {\sin x - \cos x} \right)}^2}} \right]^2} + 6{\left( {\sin x + \cos x} \right)^2} + 4\left( {{{\sin }^6}x + {{\cos }^6}x} \right)$

$ \Rightarrow 3{\left[ {{{\sin }^2}x + {{\cos }^2}x - 2\sin x\cos x} \right]^2} + 6\left[ {{{\sin }^2}x + {{\cos }^2}x + 2\sin x\cos x} \right] + 4\left[ {{{\left( {{{\sin }^2}x} \right)}^3} + {{\left( {{{\cos }^2}x} \right)}^3}} \right]$

We know that ${\sin ^2}x + {\cos ^2}x = 1$. Therefore, we get

$ \Rightarrow 3{\left[ {1 - 2\sin x\cos x} \right]^2} + 6\left[ {1 + 2\sin x\cos x} \right] + 4\left[ {{{\left( {{{\sin }^2}x} \right)}^3} + {{\left( {{{\cos }^2}x} \right)}^3}} \right]$

We know that ${a^3} + {b^3} = {\left( {a + b} \right)^3} - 3ab\left( {a + b} \right)$. Therefore, we get

$ \Rightarrow 3{\left[ {1 - 2\sin x\cos x} \right]^2} + 6\left[ {1 + 2\sin x\cos x} \right] + 4\left[ {{{\left( {{{\sin }^2}x + {{\cos }^2}x} \right)}^3} - 3{{\sin }^2}x{{\cos }^2}x\left( {{{\sin }^2}x + {{\cos }^2}x} \right)} \right]$ 

$ \Rightarrow 3\left[ {1 + 4{{\sin }^2}x{{\cos }^2}x - 4\sin x\cos x} \right] + 6\left[ {1 + 2\sin x\cos x} \right] + 4\left[ {1 - 3{{\sin }^2}x{{\cos }^2}x} \right]$

$ \Rightarrow 3 + 12{\sin ^2}x{\cos ^2}x - 12\sin x\cos x + 6 + 12\sin x\cos x + 4 - 12{\sin ^2}x{\cos ^2}x$

$ \Rightarrow 3 + 6 + 4$

$ \Rightarrow 13$

Therefore, the value of filler is $13$.

66.  Given $x > 0$, the values of $f\left( x \right) =  - 3\cos \sqrt {3 + x + {x^2}} $ lie in the interval …….

Ans: Given, $f\left( x \right) =  - 3\cos \sqrt {3 + x + {x^2}} $

Put $\sqrt {3 + x + {x^2}}  = y$ 

$ \Rightarrow f\left( x \right) =  - 3\cos y$

We know that $ - 1 \leqslant \cos y \leqslant 1$. 

$ \Rightarrow 3 \geqslant  - 3\cos y \geqslant  - 3$

$ \Rightarrow  - 3 \leqslant  - 3\cos y \leqslant 3$

Substitute value of $y$.

$ \Rightarrow  - 3 \leqslant  - 3\cos \sqrt {3 + x + {x^2}}  \leqslant 3$ 

Therefore, the value of filler is $\left[ { - 3,3} \right]$.

67.  The maximum distance of a point on the graph of the function $y = \sqrt 3 \sin x + \cos x$ from $x - axis$ is …….

Ans: Given, $f\left( x \right) =  - 3\cos \sqrt {3 + x + {x^2}} $

Or 

$ \Rightarrow y =  - 3\cos \sqrt {3 + x + {x^2}} $

We know that the maximum distance from a point on the graph from $x - axis$ is given by,

$ \Rightarrow \sqrt {{{\left( {\sqrt 3 } \right)}^2} + {{\left( 1 \right)}^2}} $ 

$ \Rightarrow \sqrt {3 + 1} $

$ \Rightarrow 2$

Therefore, the value of filler is $2$.

In each of the exercises $68$ to $75$, state whether the statements is True or False? Also give justification.

68.  If $\tan A = \dfrac{{1 - \cos B}}{{\sin B}}$, then $\tan 2A = \tan B$.

Ans: Given, $\tan A = \dfrac{{1 - \cos B}}{{\sin B}}$

We know that $1 - \cos 2A = 2{\sin ^2}A$ and $\sin 2A = 2\sin A\cos A$. Therefore, we get

$ \Rightarrow \tan A = \dfrac{{2{{\sin }^2}\dfrac{B}{2}}}{{2\sin \dfrac{B}{2}\cos \dfrac{B}{2}}}$

\[ \Rightarrow \tan A = \dfrac{{\sin \dfrac{B}{2}}}{{\cos \dfrac{B}{2}}}\]

\[ \Rightarrow \tan A = \tan \dfrac{B}{2}\]

We know that $\tan 2x = \dfrac{{2\tan x}}{{1 - {{\tan }^2}x}}$. Therefore, we get

$ \Rightarrow \tan 2A = \dfrac{{2\tan A}}{{1 - {{\tan }^2}A}}$

On substituting the value of \[\tan A = \tan \dfrac{B}{2}\], we get

$ \Rightarrow \tan 2A = \dfrac{{2\tan \dfrac{B}{2}}}{{1 - {{\tan }^2}\dfrac{B}{2}}}$

$ \Rightarrow \tan 2A = \tan B$

Thus, the given statement is true.

69.  The equality $\sin A + \sin 2A + \sin 3A = 3$ holds for some real value of $A$.

Ans: Given, $\sin A + \sin 2A + \sin 3A = 3$

We know that the maximum value of $\sin A$ is $1$. But for $\sin 2A$ and $\sin 3A$ it is not equal to $1$. Hence, it is not possible

Thus, the given statement is false.

70.  $\sin 10^\circ $ is greater than $\cos 10^\circ $.

Ans: Given, $\sin 10^\circ  > \cos 10^\circ $

$ \Rightarrow \sin 10^\circ  > \cos \left( {90^\circ  - 80^\circ } \right)$

We know that $\cos \left( {90^\circ  - \theta } \right) = \sin \theta $. Therefore, we get

$ \Rightarrow \sin 10^\circ  > \sin 80^\circ $

It is incorrect because value of $\sin e$ is in increasing order.

Thus, the given statement is false.

71.  \[\cos \dfrac{{2\pi }}{{15}}\cos \dfrac{{4\pi }}{{15}}\cos \dfrac{{8\pi }}{{15}}\cos \dfrac{{16\pi }}{{15}} = \dfrac{1}{{16}}\].

Ans: Let us start to solve \[\cos \dfrac{{2\pi }}{{15}}\cos \dfrac{{4\pi }}{{15}}\cos \dfrac{{8\pi }}{{15}}\cos \dfrac{{16\pi }}{{15}}\]

Substitute value of $\pi  = 180^\circ $.

\[ \Rightarrow \cos \dfrac{{2 \times 180^\circ }}{{15}}.\cos \dfrac{{4 \times 180^\circ }}{{15}}.\cos \dfrac{{8 \times 180^\circ }}{{15}}.\cos \dfrac{{16 \times 180^\circ }}{{15}}\]

\[ \Rightarrow \cos \dfrac{{2 \times 12^\circ }}{1}.\cos \dfrac{{4 \times 12^\circ }}{1}.\cos \dfrac{{8 \times 12^\circ }}{1}.\cos \dfrac{{16 \times 12^\circ }}{1}\]

\[ \Rightarrow \cos 24^\circ .\cos 48^\circ .\cos 96^\circ .\cos 192^\circ \]

Now, we will multiply and divide the above written expression by $16\sin 24^\circ $.

\[ \Rightarrow \dfrac{{16\sin 24^\circ }}{{16\sin 24^\circ }}\left[ {\cos 24^\circ .\cos 48^\circ .\cos 96^\circ .\cos 192^\circ } \right]\]

Above written expression can also be written as,

\[ \Rightarrow \dfrac{1}{{16\sin 24^\circ }}\left[ {\left( {2\sin 24^\circ \cos 24^\circ } \right).2\cos 48^\circ .2\cos 96^\circ .2\cos 192^\circ } \right]\]

We know that $2\sin A\cos A = \sin 2A$. Therefore, we get

\[ \Rightarrow \dfrac{1}{{16\sin 24^\circ }}\left[ {\sin \left( {2 \times 24^\circ } \right).2\cos 48^\circ .2\cos 96^\circ .2\cos 192^\circ } \right]\]

\[ \Rightarrow \dfrac{1}{{16\sin 24^\circ }}\left[ {\sin 48^\circ .2\cos 48^\circ .2\cos 96^\circ .2\cos 192^\circ } \right]\]

\[ \Rightarrow \dfrac{1}{{16\sin 24^\circ }}\left[ {\left( {2\sin 48^\circ \cos 48^\circ } \right).2\cos 96^\circ .2\cos 192^\circ } \right]\]

We know that $2\sin A\cos A = \sin 2A$. Therefore, we get

\[ \Rightarrow \dfrac{1}{{16\sin 24^\circ }}\left[ {\sin 96^\circ .2\cos 96^\circ .2\cos 192^\circ } \right]\]

\[ \Rightarrow \dfrac{1}{{16\sin 24^\circ }}\left[ {2\sin 96^\circ \cos 96^\circ .2\cos 192^\circ } \right]\]

We know that $2\sin A\cos A = \sin 2A$. Therefore, we get

\[ \Rightarrow \dfrac{1}{{16\sin 24^\circ }}\left[ {\sin 192^\circ .2\cos 192^\circ } \right]\]

\[ \Rightarrow \dfrac{1}{{16\sin 24^\circ }}\left[ {2\sin 192^\circ \cos 192^\circ } \right]\]

We know that $2\sin A\cos A = \sin 2A$. Therefore, we get

\[ \Rightarrow \dfrac{1}{{16\sin 24^\circ }}\left( {\sin 384^\circ } \right)\]

We know that $\sin 384^\circ $ can also be written as $\sin \left( {360^\circ  + 24^\circ } \right)$. Therefore, we get

\[ \Rightarrow \dfrac{1}{{16\sin 24^\circ }}\sin \left( {360^\circ  + 24^\circ } \right)\]

We know that $\sin \left( {360^\circ  + 24^\circ } \right) = \sin 24^\circ $. Therefore, we get

\[ \Rightarrow \dfrac{1}{{16\sin 24^\circ }} \times \sin 24^\circ \]

\[ \Rightarrow \dfrac{1}{{16}}\]

Hence proved L.HS. = R.H.S.

Thus, the given statement is true.

72.  One value of $\theta $ which satisfies the equation ${\sin ^4}\theta  - 2{\sin ^2}\theta  - 1$ lies between $0$ and $2\pi $.

Ans: We have, ${\sin ^4}\theta  - 2{\sin ^2}\theta  - 1$

Let $y = {\sin ^2}\theta $. Therefore, we get

$ \Rightarrow {y^2} - 2y - 1 = 0$

We know that for quadratic equation $a{x^2} + bx + c = 0$, $x = \dfrac{{ - b \pm \sqrt {{b^2} - 4ac} }}{{2a}}$. Therefore, we get

$ \Rightarrow y = \dfrac{{ - \left( { - 2} \right) \pm \sqrt {{{\left( { - 2} \right)}^2} - 4 \times 1 \times  - 1} }}{{2 \times 1}}$ 

$ \Rightarrow y = \dfrac{{2 \pm \sqrt {4 + 4} }}{2}$

$ \Rightarrow y = \dfrac{{2 \pm 2\sqrt 2 }}{2} = \dfrac{{2\left( {1 \pm \sqrt 2 } \right)}}{2}$

On canceling common terms, we get

$ \Rightarrow y = 1 \pm \sqrt 2 $

$ \Rightarrow {\sin ^2}\theta  = 1 \pm \sqrt 2 $

$ \Rightarrow {\sin ^2}\theta  = 1 + \sqrt 2 $ or ${\sin ^2}\theta  = 1 - \sqrt 2 $

We know that $ - 1 \leqslant \sin \theta  \leqslant 1$. Therefore, we say that ${\sin ^2}\theta  \leqslant 1$.

But we have, 

$ \Rightarrow {\sin ^2}\theta  = 1 + \sqrt 2 $ or ${\sin ^2}\theta  = 1 - \sqrt 2 $

Which is not possible.

Thus, the given statement is false.

73.  If $\cos ecx = 1 + \cot x$ then $x = 2n\pi ,2n\pi  + \dfrac{\pi }{2}$.

Ans: Given, $\cos ecx = 1 + \cot x$

$ \Rightarrow \dfrac{1}{{\sin x}} = 1 + \dfrac{{\cos x}}{{\sin x}}$ 

$ \Rightarrow \dfrac{1}{{\sin x}} = \dfrac{{\sin x + \cos x}}{{\sin x}}$

$ \Rightarrow \sin x + \cos x = 1$

Divide whole equation by $\sqrt 2 $.

$ \Rightarrow \dfrac{1}{{\sqrt 2 }}\sin x + \dfrac{1}{{\sqrt 2 }}\cos x = \dfrac{1}{{\sqrt 2 }}$

We know that $\sin \dfrac{\pi }{4} = \dfrac{1}{{\sqrt 2 }}$ and $\cos \dfrac{\pi }{4} = \dfrac{1}{{\sqrt 2 }}$. Therefore, we can write above  written equation as,

$ \Rightarrow \sin \dfrac{\pi }{4}\sin x + \cos \dfrac{\pi }{4}\cos x = \dfrac{1}{{\sqrt 2 }}$

Or

$ \Rightarrow \cos x\cos \dfrac{\pi }{4} + \sin x\sin \dfrac{\pi }{4} = \dfrac{1}{{\sqrt 2 }}$

We know that $\cos \left( {x - y} \right) = \cos x\cos y + \sin x\sin y$. Therefore, we get

$ \Rightarrow \cos \left( {x - \dfrac{\pi }{4}} \right) = \dfrac{1}{{\sqrt 2 }}$

$ \Rightarrow \cos \left( {x - \dfrac{\pi }{4}} \right) = \cos \dfrac{\pi }{4}$

We know that if $\cos \theta  = \cos \alpha $, then $\theta  = 2n\pi  \pm \alpha $. Therefore, we get

$ \Rightarrow x - \dfrac{\pi }{4} = 2n\pi  \pm \dfrac{\pi }{4}$

$ \Rightarrow x = 2n\pi  \pm \dfrac{\pi }{4} + \dfrac{\pi }{4}$

$ \Rightarrow x = 2n\pi  + \dfrac{\pi }{4} + \dfrac{\pi }{4}$ or $ \Rightarrow x = 2n\pi  - \dfrac{\pi }{4} + \dfrac{\pi }{4}$

$ \Rightarrow x = 2n\pi  + \dfrac{\pi }{2}$ or $ \Rightarrow x = 2n\pi $

Thus, the given statement is true.

74.  If $\tan \theta  + \tan 2\theta  + \sqrt 3 \tan \theta \tan 2\theta  = \sqrt 3 $, then $\theta  = \dfrac{{n\pi }}{3} + \dfrac{\pi }{9}$.

Ans: Given, $\tan \theta  + \tan 2\theta  + \sqrt 3 \tan \theta \tan 2\theta  = \sqrt 3 $

$ \Rightarrow \tan \theta  + \tan 2\theta  = \sqrt 3  - \sqrt 3 \tan \theta \tan 2\theta $

$ \Rightarrow \tan \theta  + \tan 2\theta  = \sqrt 3 \left( {1 - \tan \theta \tan 2\theta } \right)$

$ \Rightarrow \dfrac{{\tan \theta  + \tan 2\theta }}{{1 - \tan \theta \tan 2\theta }} = \sqrt 3 $

We know that $\dfrac{{\tan x + \tan y}}{{1 - \tan x\tan y}} = \tan \left( {x + y} \right)$. Therefore, we get

$ \Rightarrow \tan \left( {\theta  + 2\theta } \right) = \sqrt 3 $

We know that $\tan \dfrac{\pi }{3} = \sqrt 3 $. Therefore, we get

$ \Rightarrow \tan \left( {3\theta } \right) = \tan \dfrac{\pi }{3}$

We know that if $\tan \theta  = \tan \alpha $ then $\theta  = n\pi  + \alpha $, $n \in Z$

$ \Rightarrow 3\theta  = n\pi  + \dfrac{\pi }{3}$

$ \Rightarrow \theta  = \dfrac{{n\pi }}{3} + \dfrac{\pi }{9}$

Thus, the given statement is true.

75.  If $\tan \left( {\pi \cos \theta } \right) = \cot \left( {\pi \sin \theta } \right)$, then $\cos \left( {\theta  - \dfrac{\pi }{4}} \right) =  \pm \dfrac{1}{{2\sqrt 2 }}$.

Ans: Given, $\tan \left( {\pi \cos \theta } \right) = \cot \left( {\pi \sin \theta } \right)$

We know that $\tan \left( {90^\circ  - \theta } \right) = \cot \theta $. So, we can write above written equation as

$ \Rightarrow \tan \left( {\pi \cos \theta } \right) = \tan \left( {\dfrac{\pi }{2} - \pi \sin \theta } \right)$

$ \Rightarrow \pi \cos \theta  = \dfrac{\pi }{2} - \pi \sin \theta $

$ \Rightarrow \pi \cos \theta  + \pi \sin \theta  = \dfrac{\pi }{2}$

$ \Rightarrow \cos \theta  + \sin \theta  = \dfrac{1}{2}$

Divide whole equation by $\sqrt 2 $.

$ \Rightarrow \dfrac{1}{{\sqrt 2 }}\cos \theta  + \dfrac{1}{{\sqrt 2 }}\sin \theta  = \dfrac{1}{{2\sqrt 2 }}$

We know that $\sin \dfrac{\pi }{4} = \dfrac{1}{{\sqrt 2 }}$ and $\cos \dfrac{\pi }{4} = \dfrac{1}{{\sqrt 2 }}$. Therefore, we can write above  written equation as,

$ \Rightarrow \cos \dfrac{\pi }{4}\cos \theta  + \sin \dfrac{\pi }{4}\sin \theta  = \dfrac{1}{{2\sqrt 2 }}$

Or

$ \Rightarrow \cos \theta \cos \dfrac{\pi }{4} + \sin \theta \sin \dfrac{\pi }{4} = \dfrac{1}{{2\sqrt 2 }}$

We know that $\cos \left( {x - y} \right) = \cos x\cos y + \sin x\sin y$. Therefore, we get

$ \Rightarrow \cos \left( {\theta  - \dfrac{\pi }{4}} \right) =  \pm \dfrac{1}{{2\sqrt 2 }}$

Thus, the given statement is true.

76.  In the following match each item given under the column ${C_1}$ to its correct answer given under the column ${C_2}$.

1. $\sin \left( {x + y} \right)\sin \left( {x - y} \right)$  (i)    ${\cos ^2}x - {\cos ^2}y$                            

2. $\cos \left( {x + y} \right)\cos \left( {x - y} \right)$ (ii)   $\dfrac{{1 - \tan \theta }}{{1 + \tan \theta }}$ 

3. $\cot \left( {\dfrac{\pi }{4} + \theta } \right)$ (iii)  $\dfrac{{1 - \tan \theta }}{{1 + \tan \theta }}$

4. $\tan \left( {\dfrac{\pi }{4} + \theta } \right)$                                                  (iv)  ${\sin ^2}x - {\sin ^2}y$

Ans: 

1. $\sin \left( {x + y} \right)\sin \left( {x - y} \right)$

We know that $\sin \left( {x + y} \right)\sin \left( {x - y} \right) = {\sin ^2}x - {\sin ^2}y$

$\therefore (a) \leftrightarrow (iv)$ 

2. $\cos \left( {x + y} \right)\cos \left( {x - y} \right)$

We know that $\cos \left( {x + y} \right)\cos \left( {x - y} \right) = {\cos ^2}x - {\cos ^2}y$

$\therefore (b) \leftrightarrow (i)$

3. $\cot \left( {\dfrac{\pi }{4} + \theta } \right)$

We know that $\cot \left( {x + y} \right) = \dfrac{{\cot x.\cot y - 1}}{{\cot y + \cot x}}$. Therefore, we get

$ \Rightarrow \cot \left( {\dfrac{\pi }{4} + \theta } \right) = \dfrac{{\cot \dfrac{\pi }{4}.\cot \theta  - 1}}{{\cot \theta  + \cot \dfrac{\pi }{4}}}$

Substitute $\cot \dfrac{\pi }{4} = 1$ 

$ \Rightarrow \cot \left( {\dfrac{\pi }{4} + \theta } \right) = \dfrac{{\cot \theta  - 1}}{{\cot \theta  + 1}}$

Divide RHS by $\cot \theta $ 

$ \Rightarrow \cot \left( {\dfrac{\pi }{4} + \theta } \right) = \dfrac{{1 - \dfrac{1}{{\cot \theta }}}}{{1 + \dfrac{1}{{\cot \theta }}}}$

$ \Rightarrow \cot \left( {\dfrac{\pi }{4} + \theta } \right) = \dfrac{{1 - \tan \theta }}{{1 + \tan \theta }}$

$\therefore (c) \leftrightarrow (ii)$

4. $\tan \left( {\dfrac{\pi }{4} + \theta } \right)$

We know that $\tan \left( {x + y} \right) = \dfrac{{\tan x + \tan y}}{{1 - \tan x.\tan y}}$. Therefore, we get

$ \Rightarrow \tan \left( {\dfrac{\pi }{4} + \theta } \right) = \dfrac{{\tan \dfrac{\pi }{4} + \tan \theta }}{{1 - \tan \dfrac{\pi }{4}.\tan \theta }}$

Substitute $\tan \dfrac{\pi }{4} = 1$ 

$ \Rightarrow \tan \left( {\dfrac{\pi }{4} + \theta } \right) = \dfrac{{1 + \tan \theta }}{{1 - \tan \theta }}$

$\therefore (d) \leftrightarrow (iii)$

Class 11 Maths Chapter 3 Trigonometric Functions

With Vedantu solutions, the students can use trigonometric identities in different other mathematics chapters within the NCERT. This is a crucial platform for students to comprehend and memorise the core properties and identities of trigonometric functions. This chapter has been explained in a manner by Vedantu experts that students are able to attain clarity regarding the concepts and logic. If they find any difficulty, then they can get the help of experts to get on-time solutions. 

Vedantu tutors help the students get versed with the analysis of electric circuits, forecasting the height of the tides in the ocean, and evaluating a musical tone in seismology.

Vedantu enables the students to check NCERT Exemplar for Class 11 Maths - Trigonometric Functions under a single roof. All the offered solutions are helpful to build the bright future of the students. Students need to ensure from their end that they keep on regularly practising for the entire year and must not budge an inch from their focus. If this is the path they follow, then success is destined for them. 

Concepts of Chapter 3

In this chapter, students will learn and solve exemplar problems based on topics as follows:

• The relation between degree and radian

• Trigonometric functions

• Domain and range of trigonometric functions

• Sine, cosine, and tangent of some angles less than 90°

• Allied or related angles

• Functions of negative angles

• Some formulae regarding compound angles

• Trigonometric equations

• General Solution of Trigonometric Equations