Question

Write the following in the place value table.
A.$4375.756$
B.\[0.009\]
C.$15.06$
D.$74.059$
E.$8.38$
F.$3.05$

Answer 1

Hint: The place value of a digit depends upon the position of that digit in the number. If the digit is at extreme right then the number is at first position but if it is a decimal number then the number before decimal is considered to be at first position. First of all, you must go through the place value table.

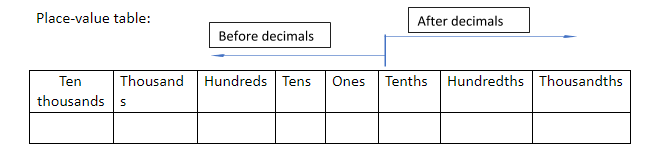
Complete step-by-step answer:
First of all, see the position of the digits in the given number and start before the decimals. The number at the first position starting from right before the decimal is at one’s place so the place value of that number is one.
The number at second position starting from right before the decimal is at tens place so the place value of that number is tens.
The number at third position starting from right before the decimal is at place so the place value of that number is thousands and so on. Look at the place value table.
If the number at first position after decimal, starting from left after decimal then the number is said to be at tenths place and so on. Look at the place value table.
Now, let's start placing the digits of the given numbers in a place value table starting with option A.
The number is 4375.756 in option A. Start from right before decimal 5 comes first so it is placed under ones, 7 comes second so it is placed under tens and so on. Start from left after decimal 7 comes first so it is placed under tenths and so on. This is as shown in table:
A.

Ten thousands	Thousands	Hundreds	Tens	Ones	Tenths	Hundredths	Thousandths
	4	3	7	5	7	5	6

The solutions for all other parts are as follow:
B.

Ten thousands	Thousands	Hundreds	Tens	Ones	Tenths	Hundredths	Thousandths
				0	0	0	9

C.

Ten thousands	Thousands	Hundreds	Tens	Ones	Tenths	Hundredths	Thousandths
			1	5	0	6

D.

Ten thousands	Thousands	Hundreds	Tens	Ones	Tenths	Hundredths	Thousandths
			7	4	0	5	9

E.

Ten thousands	Thousands	Hundreds	Tens	Ones	Tenths	Hundredths	Thousandths
				8	3	8

.

Ten thousands	Thousands	Hundreds	Tens	Ones	Tenths	Hundredths	Thousandths
				3	0	4

Note: The value of a digit is obtained by multiplying it with its place value. For example, if the place value of 4 is tens then the value of 4 is $4 \times 10 = 40$.
We can write the numbers in expandable form as follows
$ \Leftrightarrow 4375.756 = 4 \times 1000 + 3 \times 100 + 7 \times 10 + 5 \times 1 + 7 \times \dfrac{1}{{10}} + 5 \times \dfrac{1}{{100}} + 6 \times \dfrac{1}{{1000}}$