Question

Two balls are thrown horizontally from the top of a tower with velocities ${V_1}$ and \[{V_2}\] in opposite directions at the same time. After how much time the angle between the velocities of balls becomes ${90^ \circ }$?
(A) \[\dfrac{{2\sqrt {{V_1}{V_2}} }}{g}\]
(B) $\dfrac{{\sqrt {{V_1}{V_2}} }}{g}$
(C) $\dfrac{g}{{\sqrt {{V_1}{V_2}} }}$
(D) $\dfrac{g}{{\frac{{\sqrt {{V_1}{V_2}} }}{{2g}}}}$

Answer 1

Hint: When a particle is projected obliquely close to the earth’s surface, it moves at the same time within the direction of horizontal and vertical. The motion of such a particle is termed Projectile Motion. Here we will use the concept of the projectile and solve the question.

<>Formula used:
Velocity,
$ \Rightarrow V = gt$; Where $V$ is the velocity, $g$ is the acceleration due to gravity, and $t$ is the time.

Complete Step By Step Solution:

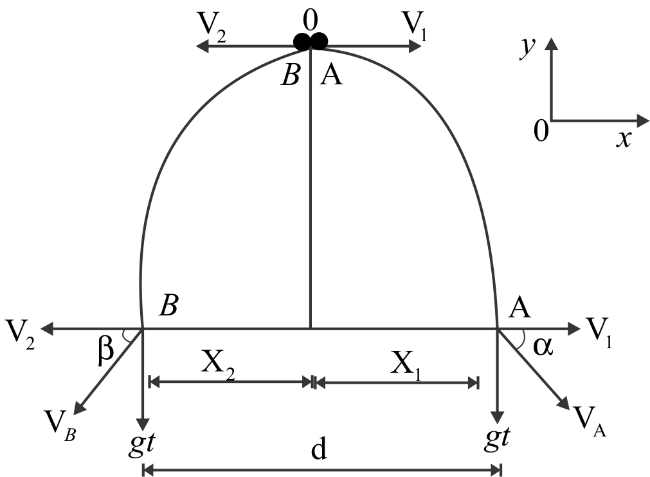
At the instant velocities of $A$ and $B$ which is being perpendicular to each other, suppose they make an angle of $\beta $ and $\alpha $ with the horizontal and the separation between them will be ${X_1} + {X_2}$.
Since each of the balls is thrown horizontally, each is acted upon a similar acceleration of gravity $g$
And they will be having constant velocities in the vertical direction which is $V = gt$. Since there's no horizontal acceleration acting upon the balls the horizontal velocities of A and B are constant as initial, that is, ${V_1}$ and ${V_2}$ respectively.
After the time $t$,
The velocity of $A$ will be,
$ \Rightarrow {\vec V_A} = {V_1}\mathop i\limits^ \wedge - gt\mathop j\limits^ \wedge $
The velocity of $B$ will be,
$ \Rightarrow {\vec V_B} = {V_2}\mathop i\limits^ \wedge - gt\mathop j\limits^ \wedge $
Since ${\vec V_A} \bot {\vec V_B}$
So the dot product of the vector will be
$ \Rightarrow {\vec V_A}.{\vec V_B} = 0$
On solving the dot product of the above vector equation, we get
$ \Rightarrow - {V_1}{V_2} + {g^2}{t^2} = 0$
$ \Rightarrow t = \dfrac{{\sqrt {{V_1}{V_2}} }}{g}$
Joining each of the vector triangles we tend to must get a triangle as A and B are perpendicular to each other at the moment.
$ \Rightarrow \alpha + \beta = {90^ \circ }$
Angle for $\alpha $ will be
$ \Rightarrow \tan \alpha = \dfrac{{gt}}{{{V_1}}}$
Angle for $\beta $ will be
$ \Rightarrow \tan \beta = \dfrac{{gt}}{{{V_2}}}$
From the formula
$
   \Rightarrow \tan \alpha \tan \beta = \tan \alpha \tan \left( {{{90}^ \circ } - \alpha } \right) = 1 \\
    \\
 $
Putting the values of both the angles,
$ \Rightarrow \dfrac{{gt}}{{{V_1}}}.\dfrac{{gt}}{{{V_2}}} = 1$
We get,
$ \Rightarrow t = \sqrt {\dfrac{{{V_1}{V_2}}}{g}} $

Therefore in $\sqrt {\dfrac{{{V_1}{V_2}}}{g}} $ time, the angle between velocities of balls becomes${90^ \circ }$.

Note: Horizontal component of initial speed is $u\cos \theta $. The initial speed in the vertical component will be $u\sin \theta $. The horizontal component of speed $u\cos \theta $ remains the same throughout the entire journey as no acceleration is acting horizontally. The vertical component of speed $u\sin \theta $ decreases step by step and becomes zero at the highest purpose of the path. At the highest purpose, the speed of the body is $u\cos \theta $ in the horizontal direction and therefore the angle between the speed and acceleration is ${90^ \circ }$.