Question

The volume of a 1m Iron rod is $1386c{m^3}$. Find the diameter of the rod.

Answer 1

Hint: Problems like these should always be understood well first. The question is asking for diameter, which means the rod in form of a cylinder. Write down the formula of volume and substitute the value of length and volume. Now solve for the one unknown in the equation.

Complete step by step solution:
Given that length $\left( l \right)$ of the rod is $1m$, i.e. $100cm$ and volume of the rod $(V)$ is $1386c{m^3}$.

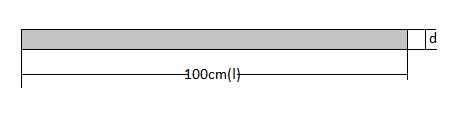
And we know that the formula for a cylindrical rod is: $V = \pi {r^2}l = \dfrac{{\pi {d^2}l}}{4}$
Where ‘$r$’ is radius and ‘$d$ ‘is the diameter of the cylinder
Let’s put all the given values in the formula and see what we get
$ \Rightarrow 1386 = \dfrac{{\pi {d^2} \times 100}}{4}$
As we know that$\pi = 3.141$, putting this value in the equation we get our equation as
$ \Rightarrow 1386 = \dfrac{{3.141 \times {d^2} \times 100}}{4}$
Now let’s simplify this to get the value of the diameter
$ \Rightarrow {d^2} = \dfrac{{1386 \times 4}}{{3.141 \times 100}}$
$ \Rightarrow {d^2} = \dfrac{{1386}}{{3.141 \times 25}}$
Taking the square-root of left and right-hand sides, we can write it like:
$ \Rightarrow d = \sqrt {\dfrac{{55.44}}{{3.141}}} \approx \sqrt {17.65} $
$\Rightarrow d = 4.2012cm$
This value will be the diameter of the required Iron rod. You can easily check the answer yourself by putting this value of diameter in the formula and calculating the volume.

$\therefore$ The diameter of the rod is $4.201 cm$

Note:
In Mensuration, never forget to notice the units of all the given data. Always convert the units in the same format before starting the solution. The alternative approach could be to use the formula $V = \pi {r^2}l$ and then finding the diameter after solving it for ‘$r$’.