Question

The perimeter of a rhombus is 100 cm. One of its diagonal is 30 cm. Find the length of the other diagonal and the area of the rhombus.

Answer 1

Hint: We will first find the length of each side of rhombus from the given perimeter of the rhombus. Use the property of rhombus and given diagonal to find the other diagonal of the rhombus. Hence, calculate the area of the rhombus.

Complete step-by-step answer:
The perimeter of the rhombus is 100 cm.
It is known that all sides of rhombus are equal.
Let the length of side of rhombus be $x$,
Then perimeter of rhombus is $4x$
Thus, $
  4x = 100 \\
  x = 25 \\
$
Hence, the length of each side of the rhombus is 25 cm.
We are given that the length of one of its diagonal is 30 cm.

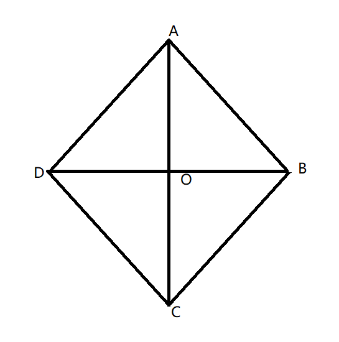
In a rhombus, diagonals are perpendicular bisectors
Let diagonals bisect at $O$.
Let $AC$ be 30 cm., then the length of \[AO\] is $\dfrac{{30}}{2} = 15$cm
Also, triangle $\Delta AOB$ is a right triangle.
Apply Pythagoras theorem in $\Delta AOB$
$A{B^2} = A{O^2} + O{B^2}$
We have $AB = 25cm$ and $AO = 15cm$,
Therefore,
$
  {\left( {25} \right)^2} = {\left( {15} \right)^2} + O{B^2} \\
  O{B^2} = {\left( {25} \right)^2} - {\left( {15} \right)^2} \\
 $
Simplifying the expression using the formula ${a^2} - {b^2} = \left( {a + b} \right)\left( {a - b} \right)$
$
  O{B^2} = {\left( {25} \right)^2} - {\left( {15} \right)^2} \\
  O{B^2} = \left( {25 + 15} \right)\left( {25 - 15} \right) \\
  O{B^2} = 40\left( {10} \right) \\
  O{B^2} = 400 \\
  OB = 20 \\
 $
Hence, the length of the other diagonal will be twice the length $OB$, which is 40units.
Next, we will find the area of the rhombus whose formula is $\dfrac{{{d_1} \times {d_2}}}{2}$, where ${d_1}$ and ${d_2}$ are the length of diagonals.
Thus, area of rhombus is,
$\dfrac{{40 \times 30}}{2} = \dfrac{{1200}}{2} = 600c{m^2}$

Note: One must be familiar with the properties of rhombus. Also, in this question, we have used Pythagoras theorem, so one must know how to apply Pythagoras theorem in any right triangle.