Question

The perimeter of a rhombus is 100 cm and one of the diagonal is 40 cm. Then the area of the rhombus is:
A. \[1000c{{m}^{2}}\]
B. \[500c{{m}^{2}}\]
C. \[1200c{{m}^{2}}\]
D. \[600c{{m}^{2}}\]

Answer 1

Hint: We know that all sides of a rhombus are equal to each other. So we can get a side by dividing the perimeter by 4. Then we will use Pythagoras theorem to find the second diagonal of the rhombus and we will use the formula of area of rhombus which is equal to \[\dfrac{1}{2}\] (products of diagonals).

Complete step-by-step answer:
We have been given the perimeter of the rhombus is 100 cm and one of the diagonals is 40 cm.
Let us suppose a rhombus ABCD having AC=40cm and their diagonal cuts at O.

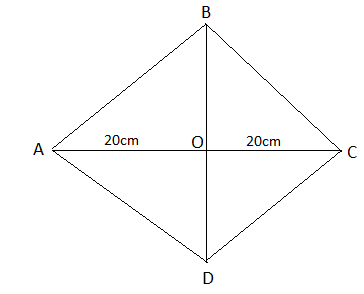
Since all the sides of a rhombus are equal to each other so we can get the side of a rhombus by dividing the perimeter by 4.
\[\Rightarrow \]Side of perimeter \[=\dfrac{100}{4}cm=25cm\]
Now in \[\Delta ABO\], we have
AB = 25cm
Since it is a side of a rhombus,
AO = 20cm
Since it is half the diagonal
Now, we know that in a right angle triangle, the square of hypotenuse is equal to the sum of the square of perpendicular and base of the triangle, known as Pythagoras theorem.
So in \[\Delta ABO\], we have
\[\begin{align}
  & A{{B}^{2}}=O{{B}^{2}}+O{{A}^{2}} \\
 & {{\left( 25 \right)}^{2}}=O{{B}^{2}}+{{\left( 20 \right)}^{2}} \\
 & 625=O{{B}^{2}}+400 \\
 & 625-400=O{{B}^{2}} \\
 & 225=O{{B}^{2}} \\
\end{align}\]
Taking square root on both the sides, we get as follows:
\[\begin{align}
  & \sqrt{225}=\sqrt{O{{B}^{2}}} \\
 & 15cm=OB \\
\end{align}\]
Hence the second diagonal \[=\left( 2\times 15 \right)cm=30cm\]
Now we have the diagonals of rhombus are 40 cm and 30 cm.
We know that area of a rhombus having diagonals \[{{d}_{1}}\] and \[{{d}_{2}}\] is given as follows:
Area \[=\dfrac{1}{2}\left( {{d}_{1}}\times {{d}_{2}} \right)\]
So, area \[=\dfrac{1}{2}\times 40\times 30c{{m}^{2}}=\dfrac{1}{2}\times 1200c{{m}^{2}}=600c{{m}^{2}}\]
Therefore, the correct option of the above question is option D.

Note: Sometimes we just substitute the value of OB = 15cm in place of the value of the second diagonal during the calculation of area of the rhombus but the diagonal is twice of the OB. So be careful at this point. Also, remember that the perimeter of any geometrical 2-D figures is equal to the sum of the length of its sides.