Question

The length and breadth of a rectangular park are in the ratio of 8:5. A path 1.5 m wide running all around the outside of an area of \[594{\text{ }}{m^2}\]. Find the dimensions of the park.

Answer 1

Hint: Firstly, by the given ratio of length and breadth of rectangular park, we get the length as 8x and breadth as 5x. As the width of the path is given, we add 2 times the width to both the length and breadth and subtract the area of rectangular path from the area of rectangular park including path, which is given as \[594{\text{ }}{m^2}\], from this equation we get the value of x, and then we get the dimensions of the park.

Complete step-by-step answer:

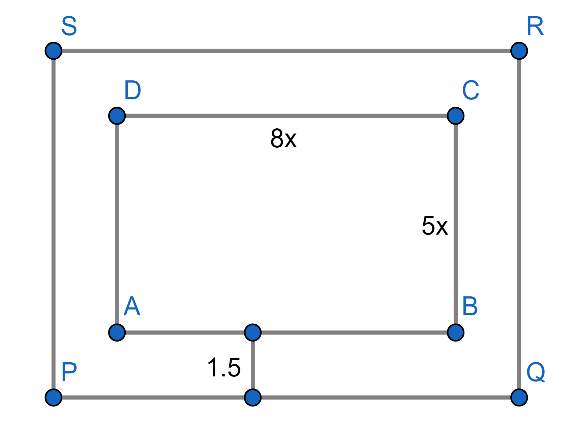
Let the length of the park rectangle ABCD be \[8x{\text{ }}m\] and the breadth of the park rectangle be \[5x{\text{ }}m\].
Now, the area of the rectangle
\[
  {\text{ = }}\left( {{\text{length of the rectangle x breadth of the rectangle}}} \right){\text{ unit}} \\
  {\text{ = }}\left( {{{8x \times 5x}}} \right){\text{ }}{{\text{m}}^{\text{2}}} \\
  {\text{ = 40}}{{\text{x}}^{\text{2}}}{\text{ }}{{\text{m}}^{\text{2}}} \\
 \]
Now, a path 1.5 m wide running all round the outside of the park. With the path, it is also a rectangle.
\[\therefore \]Length of the park (rectangle) including the path PQRS
\[ = 8x + \left( {2 \times width{\text{ }}of{\text{ }}the{\text{ }}path} \right){\text{ }}m\]
\[ = 8x + \left( {2 \times 1.5} \right){\text{ }}m\]
\[ = \left( {8x + 3} \right){\text{ }}m\]
And the breadth of the park including path PQRS
\[ = 5x + \left( {2 \times width{\text{ }}of{\text{ }}the{\text{ }}path} \right){\text{ }}m\]
\[ = 5x + \left( {2 \times 1.5} \right){\text{ }}m\]
\[ = \left( {5x + 3} \right){\text{ }}m\]
Now, the area of the park including the path i.e. PQRS
\[ = \left( {length{\text{ }}of{\text{ }}PQRS{\text{ }} \times {\text{ }}breadth{\text{ }}of{\text{ }}PQRS} \right){\text{ unit}}\]

\[
   = \left( {8x + 3} \right) \times \left( {5x + 3} \right){\text{ }}{m^2} \\
   = \left\{ {8x\left( {5x + 3} \right) + 3\left( {5x + 3} \right)} \right\}{\text{ }}{m^2} \\
   = \left( {40{x^2} + 24x + 15x + 9} \right){\text{ }}{m^2} \\
   = \left( {40{x^2} + 39x + 9} \right){\text{ }}{m^2} \\
 \]
Here, by the given problem,
\[
  Area{\text{ }}of{\text{ }}the{\text{ }}path{\text{ }} = {\text{ }}594{\text{ }}{m^2} \\
   \Rightarrow \left( {Area{\text{ }}of{\text{ }}PQRS} \right)-\left( {Area{\text{ }}of{\text{ }}ABCD} \right) = 594 \\
   \Rightarrow \left( {40{x^2} + 39x + 9} \right) - 40{x^2} = 594 \\
   \Rightarrow 39x = 594 - 9 \\
   \Rightarrow x = \dfrac{{585}}{{39}} = 15 \\
 \]
Note: We have to remember the properties and formulas of a rectangle.
Be careful about the unit when you use it. For area, it will always be \[{m^2}\]and for any length, it will be \[m\].
First draw the figure before proceeding to get a better idea of the question.