Question

Solve the system of linear equations graphically
$\begin{align}
  & 4x-5y-20=0 \\
 & 3x+5y-15=0 \\
\end{align}$
Determine the vertices of the triangle formed by the lines representing the above equations and the y-axis.

Answer 1

Hint: Here, first we have to find the two points to draw the graph of the system of equations. Next, we have to find the intersecting points of the two equations. With all the points we can draw the graph of the system of equations and y-axis. Here, the region bounded by the equations and y-axis will be a triangle. Now, from the graph we can find the vertices of the triangle.

Complete step-by-step answer:

Here, we are given with the equations:
$\begin{align}
  & 4x-5y-20=0 \\
 & 3x+5y-15=0 \\
\end{align}$
Now, we have to determine the vertices of the triangle formed by the lines representing the above equations and the y-axis.
 First consider the equation:
$4x-5y-20=0$
Now, we have to draw the line corresponding to the given equation. For that consider two points.
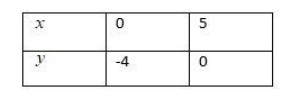
When $x=0$ we have:
$\begin{align}
  & 4\times 0-5y-20=0 \\
 & \Rightarrow -5y-20=0 \\
\end{align}$
Now, take -20 to the right side, -20 becomes 20,
$\Rightarrow -5y=20$
Next, by cross multiplication, we obtain:
$y=\dfrac{20}{-5}$
Now, by cancellation we get:
$y=-4$
Now, consider the equation $4x-5y-20=0$ when $y=0$,
$\begin{align}
  & \Rightarrow 4x-5\times 0-20=0 \\
 & \Rightarrow 4x-20=0 \\
\end{align}$
Next, by taking -20 to the right side we get:
$4x=20$
In the next step, by cross multiplication we get:
$x=\dfrac{20}{4}$
$\Rightarrow x=5$
So, we will get the table as follows:

Next, consider the equation:
$3x+5y-15=0$
Now, we have to find two points to draw the graph of the equation.
For that take $x=0$,
$\begin{align}
  & \Rightarrow 3\times 0+5y-15=0 \\
 & \Rightarrow 5y-15=0 \\
\end{align}$
Next, take -15 to the right side and it becomes 15. Hence, we will get:
$5y=15$
Now, by cross multiplication,
$\begin{align}
  & \Rightarrow y=\dfrac{15}{5} \\
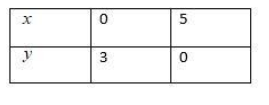
 & \Rightarrow y=3 \\
\end{align}$
Now, for $y=0$ we will obtain:
$\begin{align}
  & 3x+5\times 0-15=0 \\
 & \Rightarrow 3x-15=0 \\
\end{align}$
Next, by taking -15 to the right side it becomes 15. That is,
$\Rightarrow 3x=15$
Hence, by cross multiplication,
$\begin{align}
  & \Rightarrow x=\dfrac{15}{3} \\
 & \Rightarrow x=5 \\
\end{align}$
Therefore, we will get the table as follows.

Now, we have to draw the graph of a given system of equations.

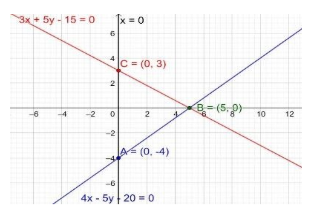
From the graph, we can say that the region bounded by the system of equations and the y-axis is a triangle $\Delta ABC$.
Hence, the vertices of $\Delta ABC$ are A (0, -4), B (5, 0) and C (0, 3)

Note: Here, at least two points you have to find to get the graph of the corresponding equations. You should also find the intersecting point of the two equations. The common region is bounded by the system of equations and y-axis which will be the triangle. The intersecting points of the equations are the vertices of the triangle.