
In any triangle $AB=2, BC=4, CA=3$ and $D$ is the midpoint of $BC$, then [Roorkee 1995]
A. $\cos B=\dfrac{11}{6}$
B. $\cos B=\dfrac{7}{8}$
C. $AD=2.4$
D. $A{{D}^{2}}=2.5$
Answer
218.1k+ views
Hint:
In this case, one side of the triangle has a mid-point $D$ which means that it divides the line into two equal parts. To find the correct relation for the provided data we will use the cosine rules and simplify the expression.
Formula Used:
Laws of cosine for triangle $ABC$ whose length is $a, b$, and $c$ respectively is given by;
$a^2 = b^2 + c^2 − 2bc.\cos A\\
b^2 = a^2 +c^2 − 2ac.\cos B\\
c^2 = a^2 + b^2 − 2ab.\cos C$.
Complete step-by-step solution:
We have given, triangle $AB=2, BC=4, CA=3$ and $D$ is the midpoint of $BC$ which means it divides $BC$ into two equal parts.
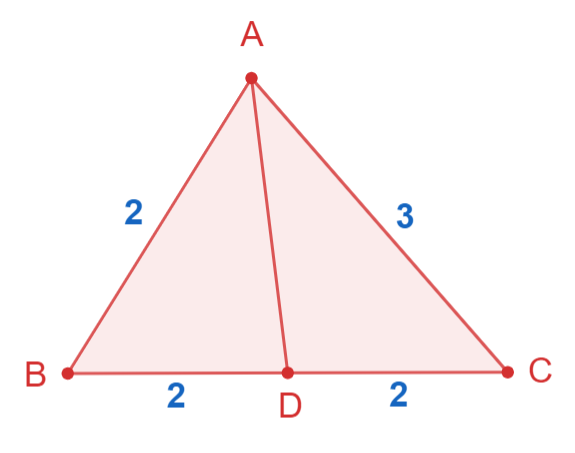
Using the law of cosine in triangle ABD we have;
$AD^2=AB^2+BD^2-2AB.BD \cos B$
Substituting values we get;
$\cos B=\dfrac{{{2}^{2}}+{{4}^{2}}-{{3}^{2}}}{2\times 2\times 4}=\dfrac{11}{16}\\
\dfrac{11}{16}=\dfrac{{{2}^{2}}+{{2}^{2}}-A{{D}^{2}}}{2\times 2\times 2}\\
\Rightarrow A{{D}^{2}}=2.5$
Hence, $A{{D}^{2}}=2.5$.
So, option D is the correct option.
Note:
Recall that a midway divides a line into two equal segments. Students frequently mistake when attempting to determine how the given data relate to one another. It will become easier to draw the triangle with the information provided. To answer this type of question, you must be familiar with the cosine rule.
Additional Information:
One of the most commonly applied properties in geometry is the triangle's angle sum property. Most often, the unknown angles are calculated using this attribute. The angle sum property of a triangle states that the sum of a triangle's three internal angles is $180$ degrees. A closed shape with both interior and exterior angles, a triangle is made up of three line segments. When the values of the other two angles are known, one can apply the angle sum property to determine the measure of an unknown interior angle.
In this case, one side of the triangle has a mid-point $D$ which means that it divides the line into two equal parts. To find the correct relation for the provided data we will use the cosine rules and simplify the expression.
Formula Used:
Laws of cosine for triangle $ABC$ whose length is $a, b$, and $c$ respectively is given by;
$a^2 = b^2 + c^2 − 2bc.\cos A\\
b^2 = a^2 +c^2 − 2ac.\cos B\\
c^2 = a^2 + b^2 − 2ab.\cos C$.
Complete step-by-step solution:
We have given, triangle $AB=2, BC=4, CA=3$ and $D$ is the midpoint of $BC$ which means it divides $BC$ into two equal parts.

Using the law of cosine in triangle ABD we have;
$AD^2=AB^2+BD^2-2AB.BD \cos B$
Substituting values we get;
$\cos B=\dfrac{{{2}^{2}}+{{4}^{2}}-{{3}^{2}}}{2\times 2\times 4}=\dfrac{11}{16}\\
\dfrac{11}{16}=\dfrac{{{2}^{2}}+{{2}^{2}}-A{{D}^{2}}}{2\times 2\times 2}\\
\Rightarrow A{{D}^{2}}=2.5$
Hence, $A{{D}^{2}}=2.5$.
So, option D is the correct option.
Note:
Recall that a midway divides a line into two equal segments. Students frequently mistake when attempting to determine how the given data relate to one another. It will become easier to draw the triangle with the information provided. To answer this type of question, you must be familiar with the cosine rule.
Additional Information:
One of the most commonly applied properties in geometry is the triangle's angle sum property. Most often, the unknown angles are calculated using this attribute. The angle sum property of a triangle states that the sum of a triangle's three internal angles is $180$ degrees. A closed shape with both interior and exterior angles, a triangle is made up of three line segments. When the values of the other two angles are known, one can apply the angle sum property to determine the measure of an unknown interior angle.
Recently Updated Pages
Chemical Properties of Hydrogen - Important Concepts for JEE Exam Preparation

JEE General Topics in Chemistry Important Concepts and Tips

JEE Atomic Structure and Chemical Bonding important Concepts and Tips

JEE Amino Acids and Peptides Important Concepts and Tips for Exam Preparation

JEE Extractive Metallurgy Important Concepts and Tips for Exam Preparation

Algebra Made Easy: Step-by-Step Guide for Students

Trending doubts
JEE Main 2026: Application Form Open, Exam Dates, Syllabus, Eligibility & Question Papers

Derivation of Equation of Trajectory Explained for Students

Hybridisation in Chemistry – Concept, Types & Applications

Understanding the Angle of Deviation in a Prism

Understanding Collisions: Types and Examples for Students

Understanding Atomic Structure for Beginners

Other Pages
JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

NCERT Solutions for Class 11 Maths Chapter 10 Conic Sections

NCERT Solutions for Class 11 Maths Chapter 9 Straight Lines

NCERT Solutions For Class 11 Maths Chapter 8 Sequences And Series

How to Convert a Galvanometer into an Ammeter or Voltmeter

NCERT Solutions For Class 11 Maths Chapter 12 Limits And Derivatives




