Question

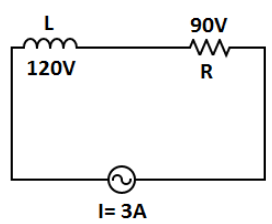
What is the impedance of the circuit shown in the figure given below?

A. $100\,ohm$
B. $50\,ohm$
C. $30\,ohm$
D. $40\,ohm$

Answer 1

Hint: Impedance is the net resistance of ac circuits when inductors, capacitors and resistors are used in a circuit. We will find the value of resistance of resistor and inductor separately and then using the formula of finding impedance which is given as $Z = \sqrt {{{({X_L})}^2} + {R^2}} $.

Complete step by step answer:
Let us first understand the impedance formula. Impedance is denoted by $Z$ and resistance of an inductor is given by ${X_L} = \dfrac{V}{I}$ since, voltage across the inductor is given in figure as ${V_{inductor}} = 120V$ . And since, current is flowing in the circuit which is given by, $I = 3A$ .

Since, both resistor and inductor are connected in series, and we also know in series circuits current flows equally in all components of circuit which means the same current $I = 3A$ will flow in both resistor and inductor. Now, the value of resistance in inductor is given by:
${X_L} = \dfrac{V}{I}$
$\Rightarrow {X_L} = \dfrac{{120}}{3}$
$\Rightarrow {X_L} = 40\,ohm \to (i)$
Now, we will find the magnitude of resistance across the resistor.

From given figure, voltage across the resistor is $90V$
$R = \dfrac{V}{I}$
$\Rightarrow R = \dfrac{{90}}{3}$
$\Rightarrow R = 30\,ohm \to (ii)$
From equations $(i)and(ii)$ we get the value of impedance as
$Z = \sqrt {{{({X_L})}^2} + {R^2}} $
Putting the values from $(i)and(ii)$ ,
$Z = \sqrt {1600 + 900} $
$\Rightarrow Z = \sqrt {2500} $
$\therefore Z = 50\,ohm$
So, the net resistance which is known as impedance is $Z = 50\,ohm$.

Hence, the correct option is B.

Note: Remember, in electrical circuit when inductor and resistor are connected in series then they are in phase difference of ${90^ \circ }$ where current lags behind the voltage by ${90^ \circ }$ and so their net impedance term of $\cos \phi $ became zero since $\cos {90^ \circ } = 0$ hence, impedance is simply the root of sum of squares of inductance and resistance.