
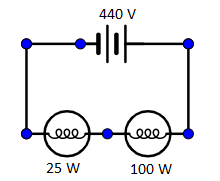
If two bulbs of $25\;{{W}}$ and $100\;{{W}}$ rated at $200\,V$ are connected in $440\,V$ supply, then
(A) $100$ watt bulb will fuse
(B) $25$ watt bulb will fuse
(C) none of the bulb will fuse
(D) both the bulbs will fuse
Answer
239.1k+ views
Hint: The resistance of each bulb will be different hence they have different powers. The voltage across each bulb has to be found using the resistance. Then the result will be compared to the voltage rating of the bulbs. By using the formula of the power, then the solution will be determined.
Complete step by step solution:
Given two bulbs having power, ${P_1} = 25\;{{W}}$ and ${P_2} = 100\;{{W}}$both are rated at voltage, $V = 200\;{{volts}}$ and connected in series with $440$ volts supply.
The expression for power is given as,
$P = \dfrac{{{V^2}}}{R}$
Where, $V$ is the voltage and $R$ is the resistance.
From the above expression,
$R = \dfrac{{{V^2}}}{P}$
Hence, we can find the resistance of each bulb using this equation for the given power and voltage rating.
$ \Rightarrow {R_1} = \dfrac{{{V^2}}}{{{P_1}}} \\
\Rightarrow \dfrac{{{{\left( {200\;{{V}}} \right)}^2}}}{{25\;{{W}}}} \\
\Rightarrow 1600\;\Omega$
The resistance of $25\;{{W}}$ bulb is $1600\;\Omega $.
And,
$\Rightarrow {R_2} = \dfrac{{{V^2}}}{{{P_2}}} \\
\Rightarrow \dfrac{{{{\left( {200\;{{V}}} \right)}^2}}}{{100\;{{W}}}} \\
\Rightarrow 400\;\Omega$
The resistance of $100\;{{W}}$ is $400\;\Omega $.
Since the two bulbs are connected in series, the total resistance will be ${R_1} + {R_2}$.
The voltage across each bulb will be different. They are connected to $440$ volts supply also.
Hence, the voltage across the $25\;{{W}}$ bulb is given as,
$\Rightarrow {V_1} = 440\;{{V}} \times \dfrac{{{R_1}}}{{{R_1} + {R_2}}}$
Substituting the values in the above expression,
$\Rightarrow {V_1} = 440\;{{V}} \times \dfrac{{1600\;\Omega }}{{1600\;\Omega + 400\;\Omega }} \\
\Rightarrow 352\;{{V}}$
The voltage across $25\;{{W}}$ is $352\;{{V}}$. This is higher than the rated voltage $200\;{{volts}}$. Therefore, the bulb will fuse.
The voltage across $100\;{{W}}$ bulb is given as,
$\Rightarrow {V_2} = 440\;{{V}} \times \dfrac{{{R_2}}}{{{R_1} + {R_2}}}$
Substituting the values in the above expression,
$\Rightarrow {V_2} = 440\;{{V}} \times \dfrac{{400\;\Omega }}{{1600\;\Omega + 400\;\Omega }} \\
\Rightarrow 88\;{{V}} $
The voltage across $100\;{{W}}$ is $88\;{{V}}$. This is lower than the rated voltage $200\;{{volts}}$. Therefore, the bulb will not fuse.
Therefore, only the $25\;{{W}}$ bulb will fuse.
The answer is option B.
Note: If two bulbs have the same voltage rating but the power is different, then a bulb having high power will have low resistance. And the low power bulb will fuse than the high power bulb. The power is directly proportional to the square of the voltage and inversely proportional to the resistance.
Complete step by step solution:
Given two bulbs having power, ${P_1} = 25\;{{W}}$ and ${P_2} = 100\;{{W}}$both are rated at voltage, $V = 200\;{{volts}}$ and connected in series with $440$ volts supply.

The expression for power is given as,
$P = \dfrac{{{V^2}}}{R}$
Where, $V$ is the voltage and $R$ is the resistance.
From the above expression,
$R = \dfrac{{{V^2}}}{P}$
Hence, we can find the resistance of each bulb using this equation for the given power and voltage rating.
$ \Rightarrow {R_1} = \dfrac{{{V^2}}}{{{P_1}}} \\
\Rightarrow \dfrac{{{{\left( {200\;{{V}}} \right)}^2}}}{{25\;{{W}}}} \\
\Rightarrow 1600\;\Omega$
The resistance of $25\;{{W}}$ bulb is $1600\;\Omega $.
And,
$\Rightarrow {R_2} = \dfrac{{{V^2}}}{{{P_2}}} \\
\Rightarrow \dfrac{{{{\left( {200\;{{V}}} \right)}^2}}}{{100\;{{W}}}} \\
\Rightarrow 400\;\Omega$
The resistance of $100\;{{W}}$ is $400\;\Omega $.
Since the two bulbs are connected in series, the total resistance will be ${R_1} + {R_2}$.
The voltage across each bulb will be different. They are connected to $440$ volts supply also.
Hence, the voltage across the $25\;{{W}}$ bulb is given as,
$\Rightarrow {V_1} = 440\;{{V}} \times \dfrac{{{R_1}}}{{{R_1} + {R_2}}}$
Substituting the values in the above expression,
$\Rightarrow {V_1} = 440\;{{V}} \times \dfrac{{1600\;\Omega }}{{1600\;\Omega + 400\;\Omega }} \\
\Rightarrow 352\;{{V}}$
The voltage across $25\;{{W}}$ is $352\;{{V}}$. This is higher than the rated voltage $200\;{{volts}}$. Therefore, the bulb will fuse.
The voltage across $100\;{{W}}$ bulb is given as,
$\Rightarrow {V_2} = 440\;{{V}} \times \dfrac{{{R_2}}}{{{R_1} + {R_2}}}$
Substituting the values in the above expression,
$\Rightarrow {V_2} = 440\;{{V}} \times \dfrac{{400\;\Omega }}{{1600\;\Omega + 400\;\Omega }} \\
\Rightarrow 88\;{{V}} $
The voltage across $100\;{{W}}$ is $88\;{{V}}$. This is lower than the rated voltage $200\;{{volts}}$. Therefore, the bulb will not fuse.
Therefore, only the $25\;{{W}}$ bulb will fuse.
The answer is option B.
Note: If two bulbs have the same voltage rating but the power is different, then a bulb having high power will have low resistance. And the low power bulb will fuse than the high power bulb. The power is directly proportional to the square of the voltage and inversely proportional to the resistance.
Recently Updated Pages
JEE Main 2025-26 Mock Tests: Free Practice Papers & Solutions

JEE Main 2025-26 Experimental Skills Mock Test – Free Practice

JEE Main 2025-26 Electronic Devices Mock Test: Free Practice Online

JEE Main 2025-26 Atoms and Nuclei Mock Test – Free Practice Online

JEE Main 2025-26: Magnetic Effects of Current & Magnetism Mock Test

JEE Main Mock Test 2025: Properties of Solids and Liquids

Trending doubts
JEE Main 2026: Session 1 Results Out and Session 2 Registration Open, City Intimation Slip, Exam Dates, Syllabus & Eligibility

Ideal and Non-Ideal Solutions Explained for Class 12 Chemistry

JEE Main Participating Colleges 2026 - A Complete List of Top Colleges

Step-by-Step Guide to Young’s Double Slit Experiment Derivation

Understanding the Angle of Deviation in a Prism

Understanding Electromagnetic Waves and Their Importance

Other Pages
CBSE Class 12 Physics Question Paper 2026: Download SET-wise PDF with Answer Key & Analysis

JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

Essential Derivations for CBSE Class 12 Physics: Stepwise & PDF Solutions

JEE Advanced 2026 - Exam Date (Released), Syllabus, Registration, Eligibility, Preparation, and More

CBSE Class 12 Physics Question Paper Set 3 (55/2/3) 2025: PDF, Answer Key & Solutions

CBSE Class 12 Physics Question Paper Set 3 (55/1/3) 2025 – PDF, Solutions & Analysis




