
Find the cube root of 27000 by prime factorisation method.
Answer
521k+ views
HINT- Proceed the solution of this question by doing prime factor of given number then try to form triplets of prime numbers, if we get triplets of all prime numbers then it will be a perfect cube and multiplication of all prime numbers will be our cube root.
Complete step-by-step answer:
We know that,
The process of cubing is similar to squaring, only that the number is multiplied three times instead of two. The exponent used for cubes is 3. for examples are 8³ = 8*8*8 = 512.
In prime factorisation method-
we will find prime factors of 27000, if it is a perfect cube and then will pair them in a group of three.
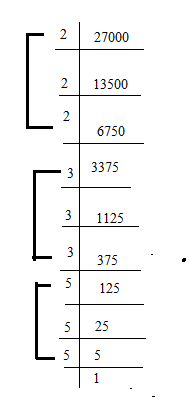
⇒27000=2×2×2×3×3×3×5×5×5
On forming pairs of three
⇒ 27000=${2^3} \times {3^3} \times {5^3}$
Since 2, 3 and 5 occurs in triplets
\[\therefore \] 27000 is a perfect cube
⇒27000=${2^3} \times {3^3} \times {5^3}$
It can be write like,
⇒27000=${\left( {2 \times 3 \times 5} \right)^3}$
On taking cube root on both side
$ \Rightarrow \sqrt[3]{{\left( {27000} \right)}} = \sqrt[3]{{{{\left( {2 \times 3 \times 5} \right)}^3}}}$
Cube root can be write raised to power $\frac{1}{3}$
\[ \Rightarrow \sqrt[3]{{27000}} = {\left( {2 \times 3 \times 5} \right)^{3 \times \frac{1}{3}}}\]
On cancelling exponential power
⇒ So cube root of 27000 = 2×3×5=30
Note- We should know that the cubic function is a one-to-one function. This is because cubing a negative number results in an answer different to that of cubing its positive counterpart. We can say this because when three negative numbers are multiplied together, two of the negatives are cancelled but one remains, so the result is also negative. 8³ = 8*8*8 = 512 and (-8) ³ = (-8) *(-8) *(-8) = -512.
Complete step-by-step answer:
We know that,
The process of cubing is similar to squaring, only that the number is multiplied three times instead of two. The exponent used for cubes is 3. for examples are 8³ = 8*8*8 = 512.
In prime factorisation method-
we will find prime factors of 27000, if it is a perfect cube and then will pair them in a group of three.
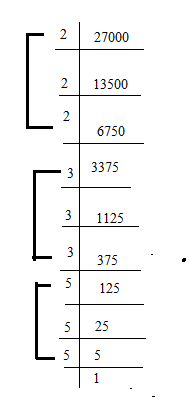
⇒27000=2×2×2×3×3×3×5×5×5
On forming pairs of three
⇒ 27000=${2^3} \times {3^3} \times {5^3}$
Since 2, 3 and 5 occurs in triplets
\[\therefore \] 27000 is a perfect cube
⇒27000=${2^3} \times {3^3} \times {5^3}$
It can be write like,
⇒27000=${\left( {2 \times 3 \times 5} \right)^3}$
On taking cube root on both side
$ \Rightarrow \sqrt[3]{{\left( {27000} \right)}} = \sqrt[3]{{{{\left( {2 \times 3 \times 5} \right)}^3}}}$
Cube root can be write raised to power $\frac{1}{3}$
\[ \Rightarrow \sqrt[3]{{27000}} = {\left( {2 \times 3 \times 5} \right)^{3 \times \frac{1}{3}}}\]
On cancelling exponential power
⇒ So cube root of 27000 = 2×3×5=30
Note- We should know that the cubic function is a one-to-one function. This is because cubing a negative number results in an answer different to that of cubing its positive counterpart. We can say this because when three negative numbers are multiplied together, two of the negatives are cancelled but one remains, so the result is also negative. 8³ = 8*8*8 = 512 and (-8) ³ = (-8) *(-8) *(-8) = -512.
Recently Updated Pages
Sam invested Rs15000 at 10 per annum for one year If class 8 maths CBSE

Magesh invested 5000 at 12 pa for one year If the interest class 8 maths CBSE

Arnavs father is 49 years old He is nine years older class 8 maths CBSE

2 pipes running together can fill a cistern in 6 minutes class 8 maths CBSE

If a man were to sell his handcart for Rs720 he would class 8 maths CBSE

By using the formula find the amount and compound interest class 8 maths CBSE

Trending doubts
What is BLO What is the full form of BLO class 8 social science CBSE

Citizens of India can vote at the age of A 18 years class 8 social science CBSE

What are the 12 elements of nature class 8 chemistry CBSE

Application to your principal for the character ce class 8 english CBSE

Full form of STD, ISD and PCO

What are gulf countries and why they are called Gulf class 8 social science CBSE




