
Construct a triangle of sides 4 cm, 5 cm and 6 cm and then a triangle similar to it whose sides are (3/5) time of the corresponding sides of the given triangle.
Answer
581.7k+ views
Hint: In this particular construction problem always have a basic gist of the ruler and compass and always construct the given construction step by step, so first draw the given triangle then draw the similar triangle. use the concepts of similar triangles to reach the solution of the question.
Complete step-by-step answer:
Given data:
Triangle having sides 4 cm, 5 cm and 6 cm.
Another similar triangle whose sides are (3/5) time of the corresponding sides of the given triangle.
Steps of construction:
$\left( i \right)$ Draw a horizontal line BC of 4 cm using a ruler.
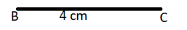
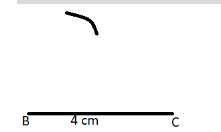
$\left( {ii} \right)$ Now take a compass with pointed end at B and make an arc with pencil end at 5 cm above line BC as shown in the below figure.
$\left( {iii} \right)$ Now again take a compass with pointed end at C and make an arc with pencil end at 6 cm above line BC, which cut the previous arc at point A as shown in the below figure, now join AB and AC.
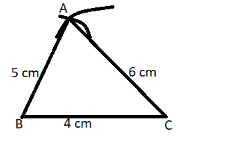
So this is the required triangle of sides 4 cm, 5 cm and 6 cm.
$\left( {iv} \right)$ Now make a line parallel to line AC from point B downwards as shown in the below figure, and on this line mark five points at interval of 1 cm as shown in the figure below.
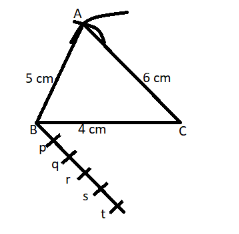
$\left( v \right)$ Now from point (r) as shown in the above figure draw a parallel line to AB which cut the line BC at point C’ and join them as shown in the figure.
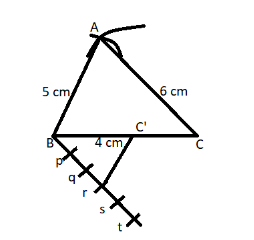
$\left( {vi} \right)$ Now from point C’ make a parallel line to AC which cuts the line AB at point A’ and join them as shown in the below figure.
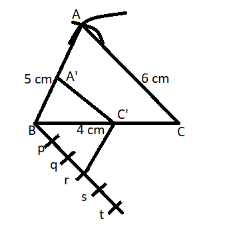
So A’BC’ is the required similar triangle whose sides are (3/5) time of the corresponding sides of the given triangle.
So this is the required triangle.
Note: Whenever we face such types of questions the key concept we have to remember is that always recall all the steps which is written above these steps are the basis of the construction without these steps we cannot draw the similar triangle, so by using these steps triangle A’BC’ is the required similar triangle whose sides are (3/5) time of the corresponding sides of the given triangle.
Complete step-by-step answer:
Given data:
Triangle having sides 4 cm, 5 cm and 6 cm.
Another similar triangle whose sides are (3/5) time of the corresponding sides of the given triangle.
Steps of construction:
$\left( i \right)$ Draw a horizontal line BC of 4 cm using a ruler.
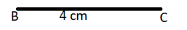
$\left( {ii} \right)$ Now take a compass with pointed end at B and make an arc with pencil end at 5 cm above line BC as shown in the below figure.

$\left( {iii} \right)$ Now again take a compass with pointed end at C and make an arc with pencil end at 6 cm above line BC, which cut the previous arc at point A as shown in the below figure, now join AB and AC.

So this is the required triangle of sides 4 cm, 5 cm and 6 cm.
$\left( {iv} \right)$ Now make a line parallel to line AC from point B downwards as shown in the below figure, and on this line mark five points at interval of 1 cm as shown in the figure below.

$\left( v \right)$ Now from point (r) as shown in the above figure draw a parallel line to AB which cut the line BC at point C’ and join them as shown in the figure.

$\left( {vi} \right)$ Now from point C’ make a parallel line to AC which cuts the line AB at point A’ and join them as shown in the below figure.

So A’BC’ is the required similar triangle whose sides are (3/5) time of the corresponding sides of the given triangle.
So this is the required triangle.
Note: Whenever we face such types of questions the key concept we have to remember is that always recall all the steps which is written above these steps are the basis of the construction without these steps we cannot draw the similar triangle, so by using these steps triangle A’BC’ is the required similar triangle whose sides are (3/5) time of the corresponding sides of the given triangle.
Recently Updated Pages
Master Class 8 Social Science: Engaging Questions & Answers for Success

Master Class 8 Maths: Engaging Questions & Answers for Success

Master Class 8 Science: Engaging Questions & Answers for Success

Class 8 Question and Answer - Your Ultimate Solutions Guide

Master Class 8 English: Engaging Questions & Answers for Success

Why are manures considered better than fertilizers class 11 biology CBSE

Trending doubts
What is BLO What is the full form of BLO class 8 social science CBSE

Citizens of India can vote at the age of A 18 years class 8 social science CBSE

Full form of STD, ISD and PCO

Right to vote is a AFundamental Right BFundamental class 8 social science CBSE

What is the difference between rai and mustard see class 8 biology CBSE

Summary of the poem Where the Mind is Without Fear class 8 english CBSE




