Question

At 2:15 o’clock, the hour and minute hands of a clock form an angle of:
A.\[{30^ \circ }\]
B.\[{5^ \circ }\]
C.\[22{\dfrac{1}{2}^ \circ }\]
D.\[7{\dfrac{1}{2}^ \circ }\]

Answer 1

Hint: We will calculate the angle formed by the hour hand and the minute hand of the clock by first finding the angle formed by minute hand with the number 12 on the clock. Then, we will find the angle formed by the hour hand from number 12 on the clock. Next, we will subtract the angle formed by the hour hand from the angle formed by the minute hand of the clock.

Complete step-by-step answer:
Suppose the hour hand and minute hand are both at the number 12. That is, the angle between them is ${0^ \circ }$
We have to find the angle at 2:15.
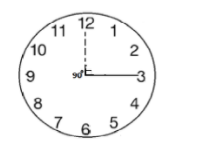
At 2:15, the minute hand will be at 3.
Now, let the minute hand move from 12 on the clock to the number 3 on the clock.
We will find the angle formed from that number 12 to number 3 on the clock.
In any perfect clock, the total angle covered by an hour hand is \[{360^ \circ }\] and there are 12 numbers in a clock. Thus, we will first find the angle between 2 numbers on a clock by dividing 360 by 12
Therefore, the angle between 2 numbers is $\dfrac{{360}}{{12}} = {30^ \circ }$
When the minute hand will come at number 3 from number 12, the angle covered will be \[3 \times {30^ \circ } = {90^ \circ }\]

Similarly, now let our hand move to number 2 on the clock.
We will now find the angle from number 12 to number 2 on the clock.
The angle between any two numbers is ${30^ \circ }$
Therefore, the angle between 12 and 2 is ${60^ \circ }$
But, when the minute hand moves, the hour hand also moves forming a certain angle every minute.
Therefore, the hour hand will be slightly away from 2
We will find the angle that is covered by an hour hand when the minute hand moves only 1 minute.
We know that when hour hand moves from one number to another, it moves \[{30^ \circ }\]
Also, 1 hour has 60 minutes.
Thus, an hour hand covers \[{30^ \circ }\] in 60 minutes.
We have to find the angle covered in 1 minute, so we will divide 60 by 30
Hence, in 1 minute the hour hand also covers ${\left( {\dfrac{{30}}{{60}}} \right)^ \circ }$ angle.
And at 2:15, the hour hand from number 2 on the clock covered ${\left( {\dfrac{{30}}{{60}}} \right)^ \circ } \times 15 = {7.5^ \circ }$
Then, the total angle covered by hour hand will be the sum of the angle covered from number 12 to number 2 and the angle covered for 15 minutes by the hour hand from number 2.
That is, \[{60^ \circ } + {7.5^ \circ } = {67.5^ \circ }\]
Now, we will calculate the angle formed by the hour hand and the minute hand at 2:15

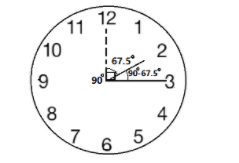
The angle between the hour hand and the minute hand at 2:15 can be calculated by subtracting the angle formed by hour hand with 12 from the angle formed by minute hand with 12.
Therefore, the angle formed by the hour hand and the minute hand at 2:15 is \[{90^ \circ } - {67.5^ \circ } = {22.5^ \circ }\]
Hence, option C is correct.


Note: The total angle formed by the clock is \[{360^ \circ }\]. Many students do not consider the movement of the hour hand when it moves for 15 minutes after 2. The hour hand also moves with each minute.