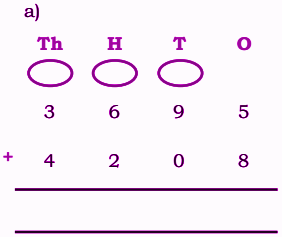
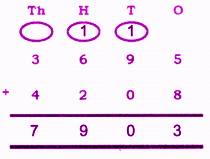
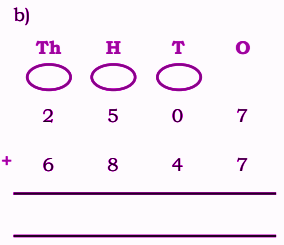
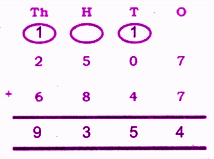
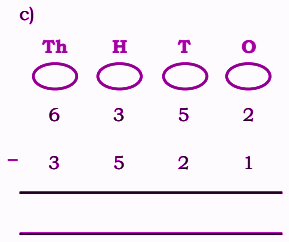
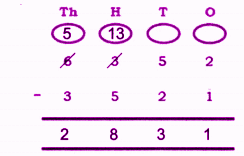
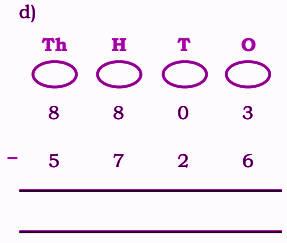
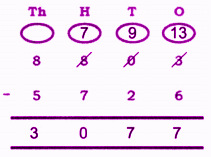
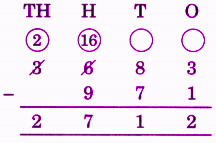
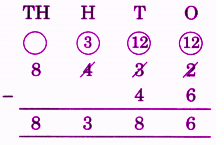
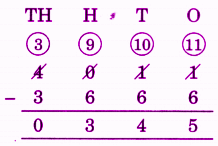
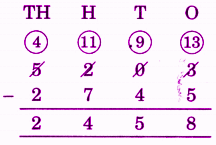
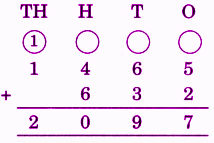
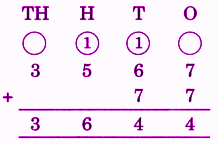
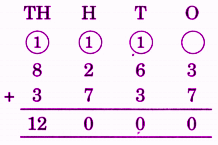
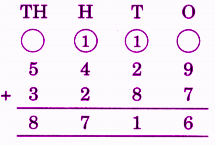
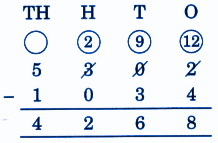
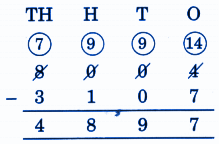
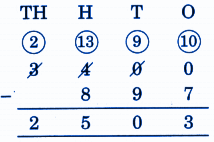
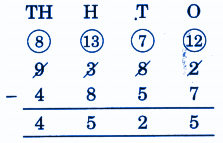
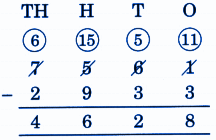
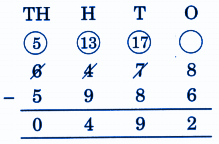
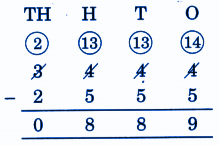
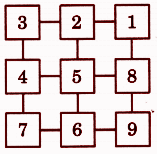
Stepwise Answers for Elephants, Tigers and Leopards (Class 4 Maths)
FAQs on NCERT Solutions For Class 4 Maths Chapter 10 Elephants Tigers And Leopards - 2025-26
1. What are the solutions for Class 4 Maths Chapter 10?
NCERT Solutions for Class 4 Maths Chapter 10 provide stepwise answers for each question based on the syllabus.
Key highlights:
- Complete solutions for all exercises in Elephants Tigers And Leopards
- Exam-ready explanations with simple steps
- Includes diagrams and definitions where necessary
- Useful for CBSE 2025–26 exam preparation
- Free PDF download for offline study
2. How to score full marks in Elephants, Tigers And Leopards?
To score full marks in Class 4 Maths Chapter 10, follow these simple tips:
- Write stepwise answers using the NCERT Solutions for Class 4 Maths Chapter 10
- Use proper mathematical words and clear diagrams
- Label all diagrams neatly
- Mention definitions and formulae where needed
- Revise using practice PDFs and sample papers
3. Is diagram important in Class 4 Chapter 10?
Yes, diagrams are important in NCERT Solutions Class 4 Maths Chapter 10 Elephants Tigers And Leopards as they help explain concepts clearly and help you earn extra marks.
- Label diagrams properly for full marks
- Neatness and correct representation are key
4. Are NCERT Solutions enough for Class 4 Maths exams?
NCERT Solutions for Class 4 Maths Chapter 10 are generally sufficient for most school exams because they match the syllabus and CBSE marking scheme.
- Practice NCERT questions thoroughly
- Revise definitions, diagrams, and solved examples
- Attempt sample papers for extra practice
5. Where to get chapterwise solutions PDF for offline study?
You can download the Class 4 Maths Chapter 10 PDF solutions for offline study from trusted educational websites.
- Free single-click PDF downloads are available
- Contains stepwise answers for every exercise
- Accessible for quick revision anytime
6. How to present long answers to match CBSE marking?
Presenting long answers for NCERT Class 4 Maths Chapter 10 should follow CBSE guidelines:
- Start with a brief introduction/definition
- Show all calculation steps neatly
- Include proper diagrams or tables where asked
- Highlight key terms and formulae
- Keep the answer structured and avoid skipping steps
7. What are the most important topics from this chapter?
The most important topics in Chapter 10 Elephants Tigers And Leopards are:
- Animal classification and counting
- Understanding bar graphs or data representation
- Simple addition and subtraction with examples
- Identification of key mathematical terms and diagrams
- Word problems based on the chapter
8. How to learn diagrams/maps for this chapter?
To learn and draw diagrams for Class 4 Maths Chapter 10:
- Practice drawing all important diagrams from the textbook and solutions
- Label every part clearly
- Use a ruler and pencil for neatness
- Study sample labelled diagrams from the PDF
9. Do examiners award partial marks for correct steps even if the final answer is wrong?
Yes, CBSE examiners often give partial marks for correct steps shown in NCERT Solutions Class 4 Maths Chapter 10—even if the final answer is incorrect.
- Always write complete working steps
- Follow the standard stepwise marking scheme
10. Are references to textbook page numbers useful during revision?
Referencing NCERT textbook page numbers during revision helps you quickly locate important topics and practice questions for Class 4 Maths Chapter 10.
- Makes self-study and targeted revision easier
- Improves exam preparation and recall
11. Which questions are likely from this chapter in school exams?
For CBSE Class 4 Chapter 10, questions are usually based on:
- Counting and grouping of animals
- Bar graphs/diagrams interpretation
- Short word problems and definitions
- Direct questions from NCERT intext and back exercises
12. How do I structure long answers for better marks?
To structure long answers in NCERT Solutions Class 4 Maths Chapter 10:
- Start with an introduction or statement of concept
- Include each calculation step clearly
- Add required diagrams, formulas, or definitions in between steps
- End with a conclusion or final answer