Euclidean Distance formula derivation solved examples and applications
The Euclidean distance, a positive number, represents the spacing between two points in a space where Euclid's geometry's axioms and theorems are true. The distance between points A and B in a Euclidean space is the length of the line segment AB belonging to the only line that passes through these points.
The space we perceive and where we human beings move is a three-dimensional space (3-D), where the axioms and theorems of Euclid's geometry are fulfilled. Two-dimensional subspaces (flats) and one-dimensional subspaces (lines) are contained in this space.
Euclidean spaces can be one-dimensional (1-D), two-dimensional (2-D), and three-dimensional (3-D).
Euclidean Distance in One Dimension
The oriented line (OX) connects all points in the one-dimensional space X, and the direction from O to X is positive.
Euclidean distance in 1 D
To locate the points on said line, the Cartesian system is used, which consists of assigning a number to each point on the line.
The Euclidean distance d(A, B) between points A and B, located on a line, is defined as the square root of the square of the differences of their X coordinates:
\[d(A,B) = \sqrt {({{({X_B} - {X_A})}^2})} \]
This definition guarantees that: The distance between two points is always a positive quantity. And that the distance between A and B is equal to the distance between B and A.
Euclidean Distance in Two Dimensions
Two-dimensional Euclidean space is a plane. The points of a Euclidean plane satisfy the axioms of Euclidean geometry, for example:
Only one line connects two points.
Three points on the plane form a triangle whose internal angles always add up to 180º.
The square of the hypotenuse in a right triangle equals the sum of the squares of its legs.
A point has X and Y coordinates in two dimensions.
For instance, the coordinates of a point P are (XP, YP), whereas those of a point Q are (XQ, YQ).
The Euclidean distance between the points P and Q is defined with the following formula:
\[d(P,Q) = \sqrt {[{{({X_Q} - {X_P})}^2} + {{({Y_Q} - {Y_P})}^2}]} \]
It should be noted that this formula is equivalent to the Pythagorean theorem, as shown in Figure 2.
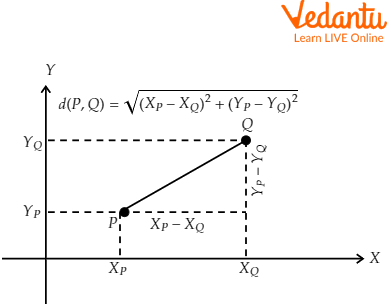
The distance between two points P and Q of the plane fulfils the Pythagorean theorem
The Euclidean Distance Formula Derivation
To derive the Euclidean distance formula, let us consider two points, A (x1, y1) and B (x1, y2) and assume that d is the distance between them. Join A and B by a line segment. We create a right-angled triangle using AB as the hypotenuse to arrive at the formula. To do this, we construct lines from points A and B that meet at point C, as illustrated below.
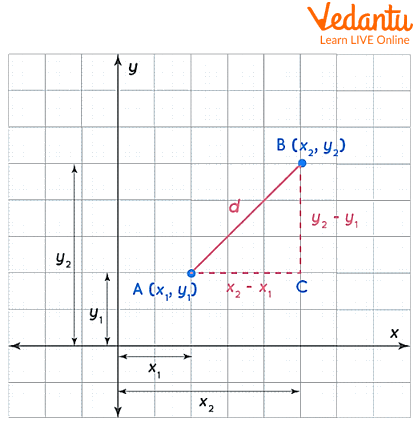
Derivation of euclidean distance formula
The Pythagorean theorem will now be applied to the triangle ABC. Then comes,
\[A{B^2} = A{C^2} + B{C^2}\]
\[{d^2} = {\left( {{x_2} - {x_1}} \right)^2} + {\left( {{y_2} - {y_1}} \right)^2}\]
Taking the square root on both sides,
\[d = \sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}} \]
Hence the Euclidean distance formula is derived.
Let’s now see some solved Euclidean distance examples.
Solved Examples
Example 1: Find the Euclidean distance between points (2,4) and (-2, -4).
Solution: Given points are (x1, y1) = (2,4) and (x2, y2) = (-2, -4)
Use Euclidean distance formula,
\[d = \sqrt {\left[ {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}} \right]} \]
\[d = \sqrt {\left[ {{{\left( { - 2 - 2} \right)}^2} + {{\left( { - 4 - 4} \right)}^2}} \right]} \]
\[d = \sqrt {{{\left( { - 4} \right)}^2} + {{\left( { - 8} \right)}^2}} \]
\[d = \sqrt {16 + 64} \]
\[d = \sqrt {80} \]
\[d = 4\sqrt 5 \] units
Example 2: Find the distance between points (1,1) and (5,4).
Sol: Given points are (x1, y1) = (1,1) and (x2, y2) = (5,5)
Use Euclidean distance formula,
\[d = \sqrt {\left[ {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}} \right]} \]
\[d = \sqrt {\left[ {{{\left( {5 - 1} \right)}^2} + {{\left( {5 - 1} \right)}^2}} \right]} \]
\[d = \sqrt {{4^2} + {4^2}} \]
\[d = \sqrt {16 + 16} \]
\[d = \sqrt {32} \,units\]
Key Features about Euclidean Distance
The Euclidean distance in mathematics is the length of a line segment connecting two points in Euclidean space.
The distance between the two locations should be calculated from the length of the line segment that connects them.
Since it could be calculated from the points' cartesian coordinates using the Pythagorean Theorem, it is frequently referred to as the Pythagorean distance.
These designations are drawn from the ancient Greek mathematicians Euclid and Pythagoras, even though Euclid did not characterise distances as numbers and the connection between the Pythagorean theorem and distance calculation was not understood until the 18th century.
Summary
The Euclid distance formula for 1 dimensional is the absolute value of the difference x-coordinates of the points. The Euclid distance of 1 dimensional is a line segment. The y-coordinate of the points is zero.
The Euclid distance formula for 2 dimensional is \[d = \sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}} \].
List of Related Articles
Practice Questions
Q 1: Find the distance between points (1,2) and (3,5) using the Euclidean distance formula.
Ans: \[\sqrt {13} \] units.
Q 2: Find the distance between points A (2,8) and B (5,8).
Ans: 3 units.
FAQs on What Is Euclidean Distance in Mathematics
1. What is Euclidean distance?
The Euclidean distance is the straight-line distance between two points in Euclidean space. It is the most common way of measuring distance in geometry and is based on the Pythagorean theorem. In a 2D plane, it represents the shortest path between two points, just like measuring distance with a ruler. It is widely used in coordinate geometry, physics, and machine learning.
2. What is the formula for Euclidean distance in 2D?
The formula for Euclidean distance in 2D between points (x₁, y₁) and (x₂, y₂) is d = √[(x₂ − x₁)² + (y₂ − y₁)²].
- Step 1: Subtract the x-coordinates.
- Step 2: Subtract the y-coordinates.
- Step 3: Square both differences.
- Step 4: Add them and take the square root.
3. How do you calculate Euclidean distance step by step?
To calculate Euclidean distance, use the distance formula derived from the Pythagorean theorem. For example, find the distance between A(1, 2) and B(4, 6).
- Subtract coordinates: (4 − 1) = 3 and (6 − 2) = 4
- Square them: 3² = 9 and 4² = 16
- Add: 9 + 16 = 25
- Square root: √25 = 5
4. What is the Euclidean distance formula in 3D?
The Euclidean distance in 3D between (x₁, y₁, z₁) and (x₂, y₂, z₂) is d = √[(x₂ − x₁)² + (y₂ − y₁)² + (z₂ − z₁)²].
- Find differences in x, y, and z.
- Square each difference.
- Add the squares.
- Take the square root.
5. Why is Euclidean distance based on the Pythagorean theorem?
Euclidean distance is based on the Pythagorean theorem because it measures the hypotenuse of a right triangle formed by coordinate differences. In 2D, the horizontal and vertical differences act as the two perpendicular sides. The formula √(a² + b²) gives the straight-line distance, which is exactly how Euclidean distance is defined in coordinate geometry.
6. What is the difference between Euclidean distance and Manhattan distance?
The key difference is that Euclidean distance measures straight-line distance, while Manhattan distance measures grid-based distance.
- Euclidean distance formula: √[(x₂ − x₁)² + (y₂ − y₁)²]
- Manhattan distance formula: |x₂ − x₁| + |y₂ − y₁|
7. Can Euclidean distance be used in higher dimensions?
Yes, Euclidean distance can be calculated in any number of dimensions using the general formula d = √[(x₁ − y₁)² + (x₂ − y₂)² + ... + (xₙ − yₙ)²].
- Subtract corresponding coordinates.
- Square each difference.
- Add all squared terms.
- Take the square root.
8. What are some real-life applications of Euclidean distance?
Euclidean distance is used to measure straight-line distance in many real-world applications.
- Geometry: Finding distance between points.
- Physics: Calculating displacement.
- Machine learning: Measuring similarity between data points.
- GPS and mapping: Estimating shortest paths.
9. Is Euclidean distance always positive?
Yes, Euclidean distance is always non-negative (d ≥ 0) because it is the square root of a sum of squared numbers. Squares are always zero or positive, so their sum cannot be negative. The distance equals 0 only when the two points are identical.
10. What are common mistakes when calculating Euclidean distance?
Common mistakes when calculating Euclidean distance usually involve errors in subtraction or squaring.
- Forgetting to square the coordinate differences.
- Mixing up x and y coordinates.
- Adding differences before squaring.
- Forgetting the final square root.
