How to Subtract Mixed Numbers Using Proper Steps and Worked Examples
What are Mixed Numbers? Learn About the Subtraction of These Numbers
Before we start our study on the topic of subtraction of mixed numbers, first let us get into the basics. What are Mixed Numbers? Mixed Numbers are the other name for mixed fractions. These are the fractions that are more than the whole number. Want to have more clarity on mixed fractions? Then refer to the example after this section.
Here we will talk about subtracting these mixed numbers or mixed fractions.
Example of Mixed Numbers or Mixed Fractions
As already discussed, mixed numbers or mixed fractions are numbers that are more than just the whole numbers. Example: Renu has 3 chocolates, and each chocolate has 3 bars. She ate 7 bars of chocolate. This means that 2 full chocolate and 1 bar of the third chocolate she had eaten. This can be represented in the following diagram:
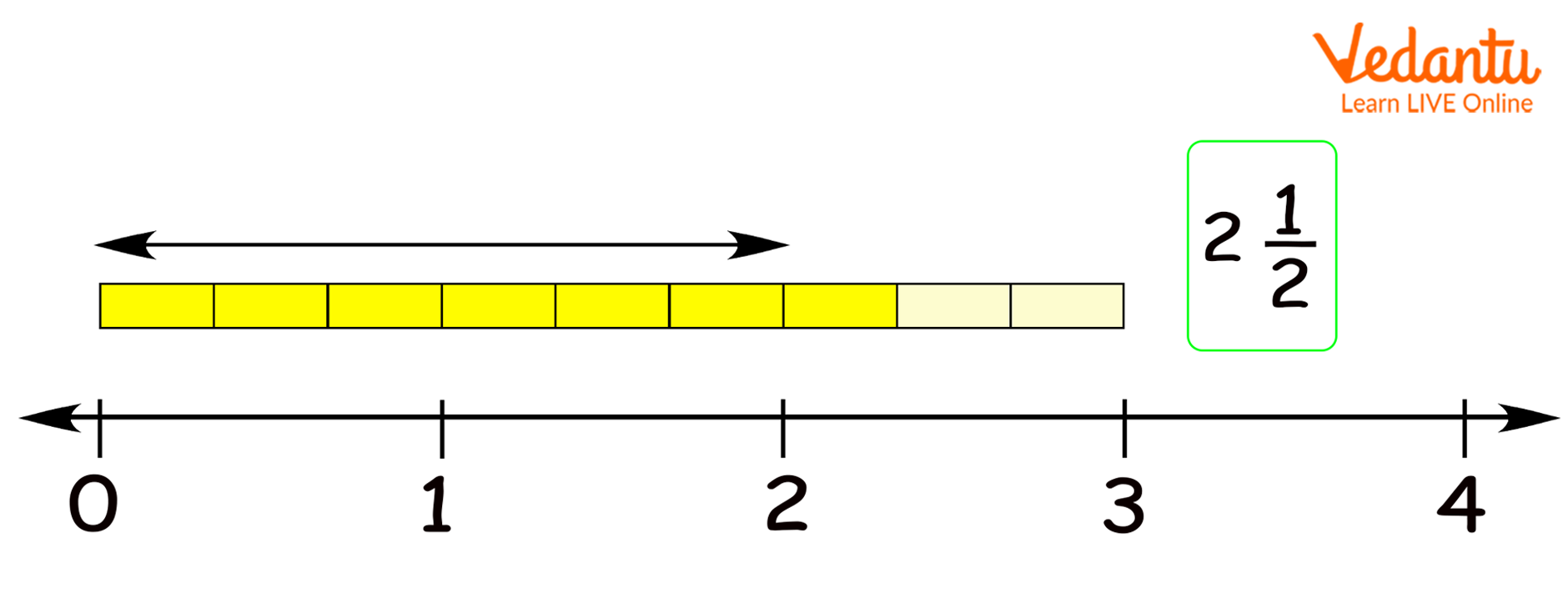
Some real-life examples of mixed numbers are presented in the diagram given below:
After gaining the basics of mixed numbers we will discuss the subtraction of these mixed numbers.
How do you Subtract the Mixed Numbers?
We can subtract the mixed numbers in the same manner as to how we add the mixed numbers. Let us check the operation of subtracting mixed numbers step by step. In this, we will be dividing the steps into two cases. In Case I, we will talk about how to subtract the mixed numbers with the same denominator. In Case II, we will discuss the steps involved in the subtraction of the mixed numbers with different denominators.
Case 1: Subtracting mixed numbers with the same denominators.
Follow the simple steps to subtract the mixed numbers with the same denominators:
Step 1: First subtract the whole numbers.
Step 2: Now convert the fractions into the improper fractions.
Step 3: Now subtract the fractions.
Step 4: You can change the improper fraction into mixed numbers if required
Step 5: Now write the mixed numbers in whole and also the fractions.
Also, cite the example to understand the steps better.
Example: 4 4⁄3 - 2 2⁄3
Step 1 - Subtract 4 from 2.
4 - 2 =2
Step 2 - Subtract the fractions:
4⁄3 - 2⁄3 = ⅔
Step 3 - Write the fraction with the whole.
4 4⁄3 - 2 2⁄3 = 2 2⁄3
Now, we will check Case 2 where the mixed numbers are subtracted with different denominators.
Case 2: Subtraction of the mixed numbers with different denominators.
Step 1: Firstly convert the mixed numbers with the different denominators.
Step 2: Now we have to find the common multiple of both the denominators.
Step 3: Convert the fractions as the common denominators.
Step 4: Now solve the fractions likewise.
Step 5: Convert the fractions into mixed numbers.
Let us check the example to understand with more clarity
Example 2: 6 1⁄2 - 1 3⁄4
Step 1 - Here we have to convert the mixed numbers into the form of improper fractions.
13⁄2 - 7⁄4
Step 2 - Then find the common multiple of both these denominators 2 and 4.
The Common multiple of 2 and 4 is 4.
Step 3 - Thereby convert the fractions as the common denominators.
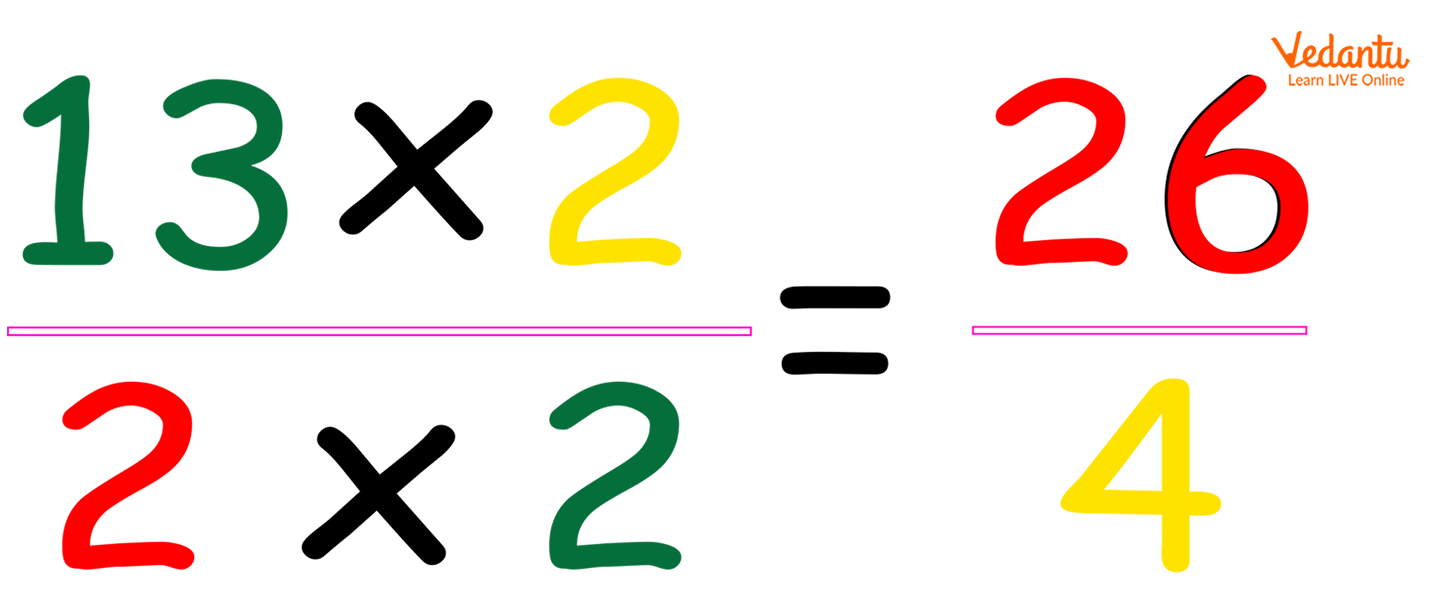
Step 4 - Now solve the fractions
26⁄4 - 7⁄4 = 19⁄4
Step 5 - After this convert the fraction into the mixed number form.
19⁄4 = 4 3⁄4
Did You Know?
We can multiply a fraction by any number but the value of the fraction will always remain the same.
As we come to the end of our discussion, we hope now it is clear what are mixed fractions and you can thereby solve the mixed fractions if it is in the subtraction form. You can practice as many sums as you like to be clearer on this part.
FAQs on Subtraction of Mixed Numbers Explained with Simple Methods
1. What is subtraction of mixed numbers?
Subtraction of mixed numbers means finding the difference between two numbers that each have a whole number and a proper fraction.
- A mixed number is written as a whole number and a fraction, such as 3 1/2.
- To subtract mixed numbers, subtract the whole numbers and fractions separately (after making denominators the same if needed).
- If the fraction of the first number is smaller, you may need to borrow or regroup from the whole number.
2. How do you subtract mixed numbers step by step?
To subtract mixed numbers, first subtract the fractions and whole numbers separately, regrouping if necessary.
- Step 1: Make the fractional parts have a common denominator.
- Step 2: Subtract the fractions.
- Step 3: Subtract the whole numbers.
- Step 4: Simplify the final answer.
- Example: 5 3/4 − 2 1/4 = (5 − 2) + (3/4 − 1/4) = 3 1/2.
3. How do you subtract mixed numbers with different denominators?
To subtract mixed numbers with different denominators, first convert the fractions to equivalent fractions with a common denominator.
- Find the least common denominator (LCD).
- Rewrite each fraction with the LCD.
- Subtract the fractions and then the whole numbers.
- Example: 4 1/3 − 2 1/6 → LCD is 6 → 4 2/6 − 2 1/6 = 2 1/6.
4. How do you subtract mixed numbers with borrowing?
You subtract mixed numbers with borrowing by regrouping 1 whole into a fraction when the top fraction is smaller than the bottom fraction.
- Example: 3 1/4 − 1 3/4.
- Since 1/4 is smaller than 3/4, borrow 1 from 3.
- 3 1/4 becomes 2 5/4.
- Now subtract: (2 − 1) + (5/4 − 3/4) = 1 1/2.
5. Can you give an example of subtracting mixed numbers?
An example of subtracting mixed numbers is 6 2/5 − 3 1/5 = 3 1/5.
- The denominators are already the same (5).
- Subtract fractions: 2/5 − 1/5 = 1/5.
- Subtract whole numbers: 6 − 3 = 3.
- Combine the results to get 3 1/5.
6. Is it easier to convert mixed numbers to improper fractions when subtracting?
Yes, converting mixed numbers to improper fractions can make subtraction easier, especially when borrowing is required.
- Convert each mixed number to an improper fraction.
- Find a common denominator if needed.
- Subtract the numerators.
- Example: 2 1/2 − 1 3/4 → 5/2 − 7/4 → 10/4 − 7/4 = 3/4.
7. What is the formula for subtracting mixed numbers?
There is no single formula, but the general rule is to subtract whole numbers and fractions separately after making denominators equal.
- (a b/c) − (d e/f)
- Step 1: Convert fractions to a common denominator.
- Step 2: Subtract fractions and whole numbers.
- Step 3: Regroup if the fraction is negative.
8. What are common mistakes when subtracting mixed numbers?
Common mistakes when subtracting mixed numbers include forgetting to find a common denominator and not borrowing correctly.
- Not using the least common denominator (LCD).
- Subtracting denominators directly (which is incorrect).
- Forgetting to regroup when needed.
- Not simplifying the final answer.
9. How do you subtract mixed numbers with unlike denominators and borrowing?
To subtract mixed numbers with unlike denominators and borrowing, first find a common denominator, then regroup if necessary.
- Example: 5 1/3 − 2 3/4.
- LCD of 3 and 4 is 12.
- Rewrite: 5 4/12 − 2 9/12.
- Borrow: 5 4/12 becomes 4 16/12.
- Subtract: (4 − 2) + (16/12 − 9/12) = 2 7/12.
10. How do you check your answer when subtracting mixed numbers?
You can check your answer by adding the difference to the smaller mixed number to see if you get the original larger number.
- If A − B = C, then check by verifying C + B = A.
- Example: If 4 1/2 − 2 1/4 = 2 1/4, then 2 1/4 + 2 1/4 = 4 1/2.
- If the sum matches the original number, the subtraction is correct.
