




Key Differences Between Sets, Relations, and Functions
Sets, relations, and functions are formal structures in mathematics used to classify objects, establish connections among elements, and describe rules associating elements of different collections.
Mathematical Definition and Description of Sets
Definition: A set is a well-defined collection of distinct objects, represented by listing its elements within curly brackets, for example, $A = \{1, 2, 3\}$, or by set-builder notation, such as $B = \{x \mid x \text{ is a prime } \leq 10\}$.
Cardinality of a set is denoted as $n(A)$ and represents the number of elements in set $A$.
The empty set (or null set) contains no elements, denoted as $\varnothing$ or $\{\}$.
A singleton set contains exactly one element.
- Finite and infinite sets
- Power set and its cardinality
- Universal and equal sets
- Subset and proper subset
If $A$ has $n$ elements, the power set $P(A)$ comprises all $2^{n}$ possible subsets of $A$.
Standard Set Operations and Algebraic Laws
Union ($A \cup B$), intersection ($A \cap B$), and difference ($A \setminus B$) are the primary operations on sets, with the universal set $U$ providing the context for complements $A' = U \setminus A$.
- Commutative, associative, distributive laws
- De Morgan's laws for complements
- Identity, null, and idempotent laws
De Morgan's laws state $(A \cup B)' = A' \cap B'$ and $(A \cap B)' = A' \cup B'$.
Structure of Ordered Pairs and Cartesian Products
An ordered pair $(a,b)$ consists of elements $a$ and $b$ from sets $A$ and $B$, where order matters, i.e., $(a,b) \neq (b,a)$ unless $a=b$.
The Cartesian product $A \times B$ is defined as the set $\{(a, b) \mid a \in A,\, b \in B\}$, which forms the foundation for defining relations and functions.
Definition and Classification of Mathematical Relations
Definition: Any subset $R$ of $A \times B$ is called a relation from $A$ to $B$; if $A = B$, $R$ is a relation on $A$.
- Domain and range of a relation
- Inverse and identity relations
- Empty, universal, and equivalence relations
Domain $D(R) = \{a \in A \mid \exists b \in B, (a,b) \in R\}$, and range $R(R) = \{b \in B \mid \exists a \in A, (a,b) \in R\}$.
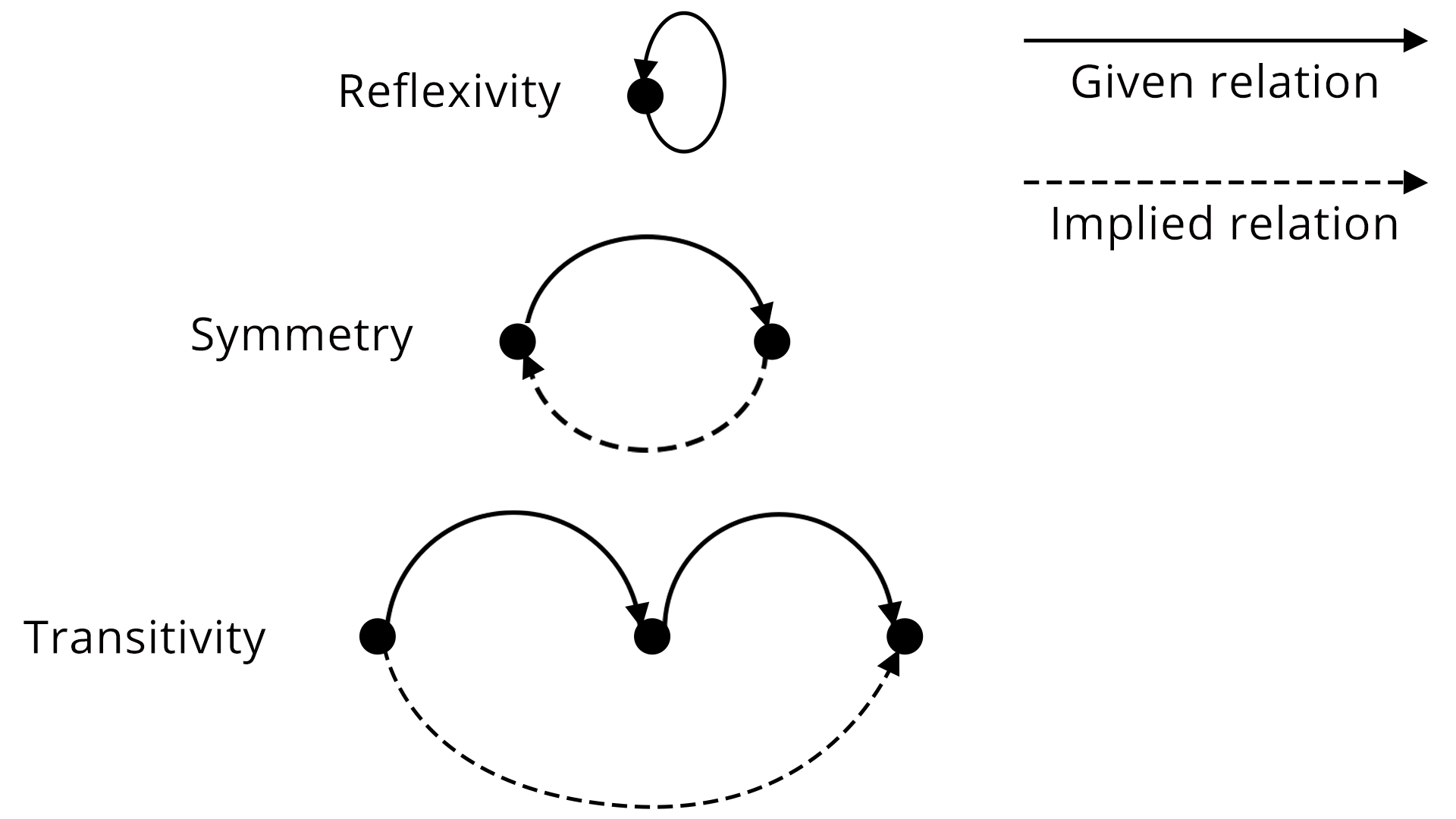
A relation is reflexive if $(a,a) \in R\, \forall a \in A$; symmetric if $(a,b)\in R \implies (b,a)\in R$; transitive if $(a,b)\in R$ and $(b,c)\in R \implies (a,c)\in R$. A relation is equivalence if it is reflexive, symmetric, and transitive.
For further relations question types, see Sets Relations And Functions Important Questions.
Mathematical Formulation of Functions and Mappings
Definition: A function $f$ from $A$ to $B$ (notation: $f : A \to B$) is a special relation where every $a \in A$ is associated with a unique $b \in B$, written $b = f(a)$.
- Domain, codomain, and range of a function
- Types: injective, surjective, bijective functions
- One-one, onto, many-one, into, constant functions
A function $f$ is injective if $f(a_{1}) = f(a_{2}) \implies a_{1} = a_{2}$ for all $a_{1}, a_{2} \in A$. It is surjective if for all $b \in B$, there exists $a \in A$ such that $f(a) = b$. It is bijective if both injective and surjective.
Constant functions map each element of $A$ to the same value in $B$. For in-depth functional forms, visit Functions And Its Types.
Principal Results Including Counting and Inclusion-Exclusion
Result: For two finite, possibly overlapping sets $A$ and $B$, the cardinality of their union is $n(A \cup B) = n(A) + n(B) - n(A \cap B)$. For three sets:
$n(A \cup B \cup C) = n(A) + n(B) + n(C) - n(A \cap B) - n(A \cap C) - n(B \cap C) + n(A \cap B \cap C)$
This counting principle is fundamental to problems in Permutations And Combinations and Probability.
- Inclusion-exclusion principle
- Number of subsets and possible relations
- Inverse of bijective functions
- Number of functions between finite sets
Worked Examples Based on Sets, Relations, and Functions
Example: Given $A = \{1, 2, 3\}$, $B = \{4, 5\}$, the Cartesian product $A \times B = \{(1,4), (1,5), (2,4), (2,5), (3,4), (3,5)\}$.
Direct substitution produces 3 elements in $A$, and 2 in $B$, so there are $3 \times 2 = 6$ ordered pairs.
Example: Let $R$ be the relation of divisibility from $A = \{3,5,7\}$ to $B = \{6,12,5,9\}$, i.e., $R = \{(a,b) | a \mid b\}$. By checking divisibility, $R = \{(3,6), (3,12), (3,9), (5,5)\}$.
Domain is $\{3,5\}$, codomain is $\{6,12,5,9\}$, and range is $\{6,12,5,9\}$.
Example: If $f(x) = \sin^{-1}x$, $g(x) = \frac{x^2-x-2}{2x^2-x-6}$, find domain of $f\circ g$. Solution: Solve $|g(x)| \leq 1$. This leads to $(x+1)^2 \leq (2x+3)^2$, or $3x^2 + 10x + 8 \geq 0$, i.e., $x \in (-\infty, -2] \cup \left[-\frac{4}{3}, \infty\right)$. Therefore, the domain is $(-\infty, -2] \cup \left[-\frac{4}{3}, \infty\right).$
For additional practice, consult Sets Relations And Functions Practice Paper.
Exam Cues and Typical Misconceptions
Exam Tip: When verifying if a relation is an equivalence relation, check all three properties (reflexivity, symmetry, transitivity) with full generality, not only for sample pairs.
A frequent error is confusing range and codomain: the range is always a subset of the codomain.
When evaluating the inverse of a function, ensure the original function is bijective; otherwise, an inverse does not exist as a function.
Always specify the reference universal set when discussing complements or operations involving complements.
For stepwise notes on all definitions and properties, refer to Sets Relations And Functions Revision Notes.
Understanding Sets, Relations, and Functions in Mathematics

 Share
ShareFAQs on Understanding Sets, Relations, and Functions in Mathematics
1. What are sets in mathematics?
Sets in mathematics are well-defined collections of distinct objects, considered as a whole.
- A set is denoted by capital letters (A, B, C, etc.) and its elements are listed in curly brackets: A = {1, 2, 3}.
- Common examples include the set of natural numbers, integers, or vowels in the English alphabet.
- Sets are foundational in mathematics and frequently appear in CBSE and exam questions.
2. What is the difference between relations and functions?
Relations describe the association between elements of two sets, while functions are special types of relations with unique output for every input.
- A relation pairs elements from set A with set B.
- A function pairs each element of set A with exactly one element of set B.
- Every function is a relation, but not every relation is a function.
- Mastering this difference is essential for CBSE board and entrance exam success.
3. What are the types of sets with examples?
There are several types of sets in mathematics, each defined by its properties.
- Null/Empty Set: Contains no elements, e.g., { } or ∅.
- Finite Set: Has a definite number of elements, e.g., {2, 4, 6}.
- Infinite Set: Contains uncountable elements, e.g., the set of all integers.
- Subset: Every element belongs to another set, e.g., {a, b} is a subset of {a, b, c}.
- Equal Sets: Contain exactly the same elements, e.g., {2, 3} and {3, 2}.
4. What are the main properties of relations?
Relations in mathematics have several important properties that help classify them.
- Reflexive Relation: Every element is related to itself.
- Symmetric Relation: If a is related to b, then b is related to a.
- Transitive Relation: If a is related to b and b to c, then a is related to c.
- Relations satisfying all three are called equivalence relations.
5. What defines a function as one-one (injective), onto (surjective), or bijective?
A function is classified based on how elements are mapped:
- One-one (Injective): Every element has a unique image, no two elements share the same output.
- Onto (Surjective): Every element in the output set is the image of at least one input.
- Bijective: The function is both injective and surjective, meaning a perfect pairing between sets.
6. What are the basic operations on sets?
Set operations are used to combine or relate sets in different ways.
- Union (A ∪ B): Combines all elements from both sets.
- Intersection (A ∩ B): Includes only elements present in both sets.
- Difference (A − B): Elements in A not in B.
- Complement (A'): Elements not in A, considering the universal set.
7. What is the domain, co-domain, and range of a function?
The domain, co-domain, and range are key concepts for describing functions.
- Domain: The set of all possible input values.
- Co-domain: The set in which all outputs must lie.
- Range: Actual set of outputs produced by the function.
8. How are sets used to represent real-life situations?
Sets can model groups, categories, and relationships in real-life scenarios.
- Classifying student groups based on subjects chosen.
- Representing survey data, such as those who like cricket or football.
- Organizing events with set operations for overlapping activities.
9. What are common Venn diagram representations of sets?
Venn diagrams visually represent relationships among sets.
- Circular diagrams illustrate union, intersection, and complement of sets.
- Two or three set Venn diagrams are commonly used for CBSE examinations.
- They simplify problem-solving by showing set operations pictorially.
10. Why is the study of relations and functions important?
Relations and functions are foundational concepts in mathematics, vital for advanced study and real-world problem-solving.
- They provide a way to model connections between variables.
- Understanding them is crucial for calculus and higher mathematics.
- They appear frequently in board and entrance exams like CBSE, JEE, and others.
11. Define universal set and give an example.
Universal set contains all objects under consideration for a particular discussion.
- It is denoted by the symbol U.
- Example: For the sets of vowels and consonants, the set of all English alphabets is the universal set.
12. How do you prove a function is bijective?
To prove a function is bijective, you must show it is both injective (one-one) and surjective (onto).
- Demonstrate that each element in the domain maps to a unique element in the co-domain (injective).
- Show that every element in the co-domain has a pre-image in the domain (surjective).
- If both conditions are met, the function is bijective.




















 Watch Video
Watch Video


