Properties of Parabola

A parabola is a graph of a function of quadratic type. It is usually of an approximate U shape or is mirror-symmetrical. A parabola can be referred to as an equation of a curve, such that a point on the curve is at an equal distance from a fixed point and a fixed line. This fixed point is the focus of the parabola, and the fixed line is called the directrix of the parabola. A point to note is that the fixed point does not lie on the fixed line. A locus of any point which is equidistant(at an equal distance) from a given point (focus) and a given line (directrix) is called a parabola.

General Equation of Parabola

The general equation of a parabola is: $y=a(x-h)^{2}+k$ or $x=a(y-k)^{2}+h$, where $(h,k)$ denotes the coordinates of the vertex. The standard equation of the parabola is $y^{2}=4ax$.

Standard Equations of Parabola

Here, we can see four standard equations of a parabola. These four standard forms are based on the axis and the orientation of the parabola. The transverse axis and the conjugate axis of these parabolas are referred to in different ways in each standard form parabola.

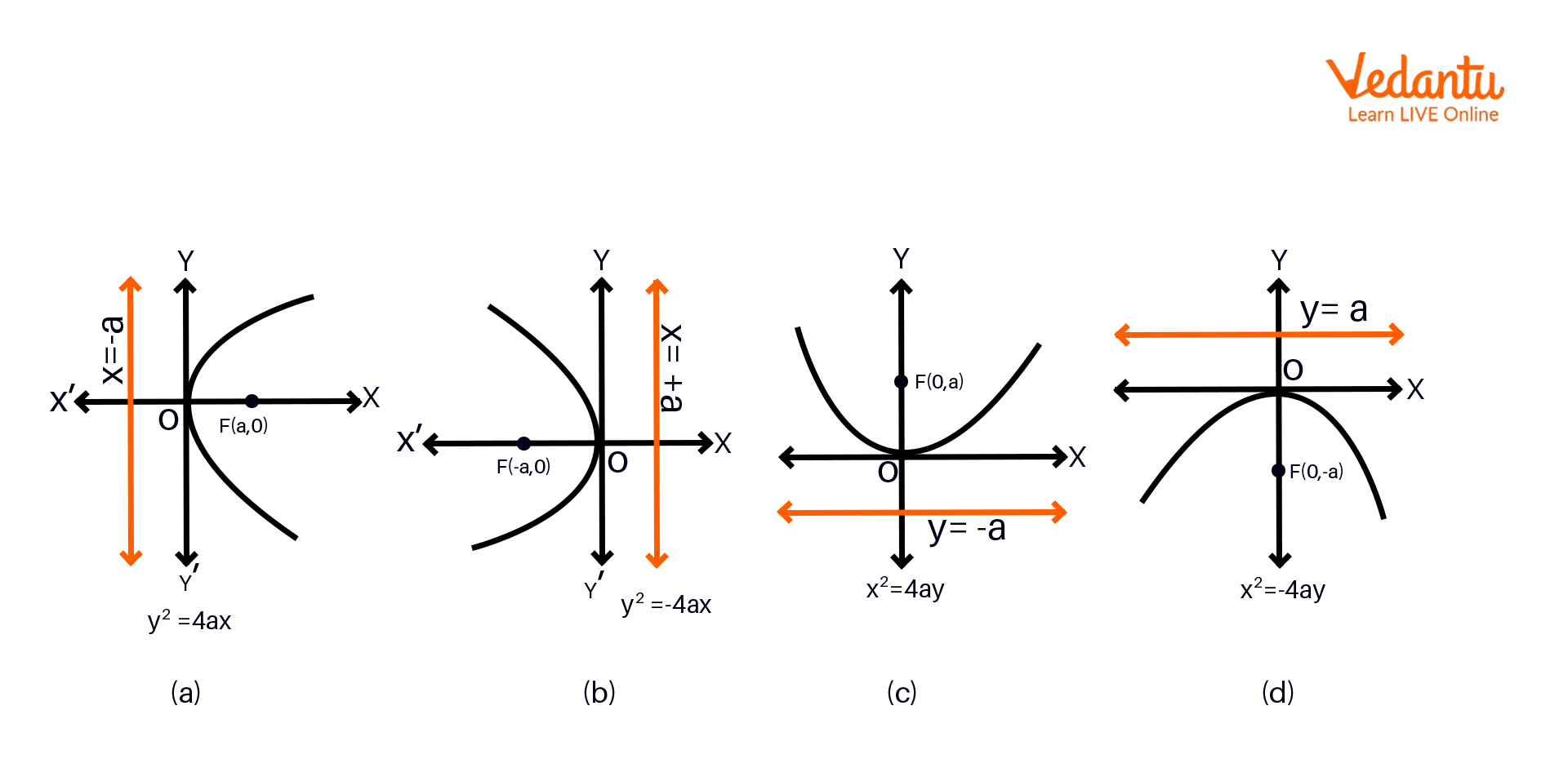
Four standard parabola curves

$y^{2}=4ax$

$y^{2}=-4ax$

$x^{2}=4ay$

$x^{2}=-4ay$

The following observations can be made from the standard form equations of parabolas:

• Parabola is symmetric concerning its axis. If the equation has the term of $y^{2}$, then the axis of symmetry will be along the x-axis in the curve, and if the equation has the term with $x^{2}$, then the axis of symmetry will be along the y-axis in the parabola curve.

• If the axis of symmetry is along the x-axis, then the parabola will open to the right if the coefficient of the x is positive and will open to the left if the coefficient of x is negative.

• If the axis of symmetry is along the y-axis, the parabola opens upwards if the coefficient of y is +ve and opens downwards if the coefficient of y is -ve.

Curves for the Four Standard Parabola

Four standard parabola equations have the following curves as shown in the respective figures below.

• The parabola $y^{2}=4ax$ represents the curve in figure no. a below.

• The parabola $y^{2}=-4ax$ represents the curve in figure no. b below.

• The parabola $x^{2}=4ay$ represents the curve in figure no. c below.

• The parabola $x^{2}=-4ay$ represents the curve in figure no. d below.

Standard Parabol

Important Terms Related to Parabola

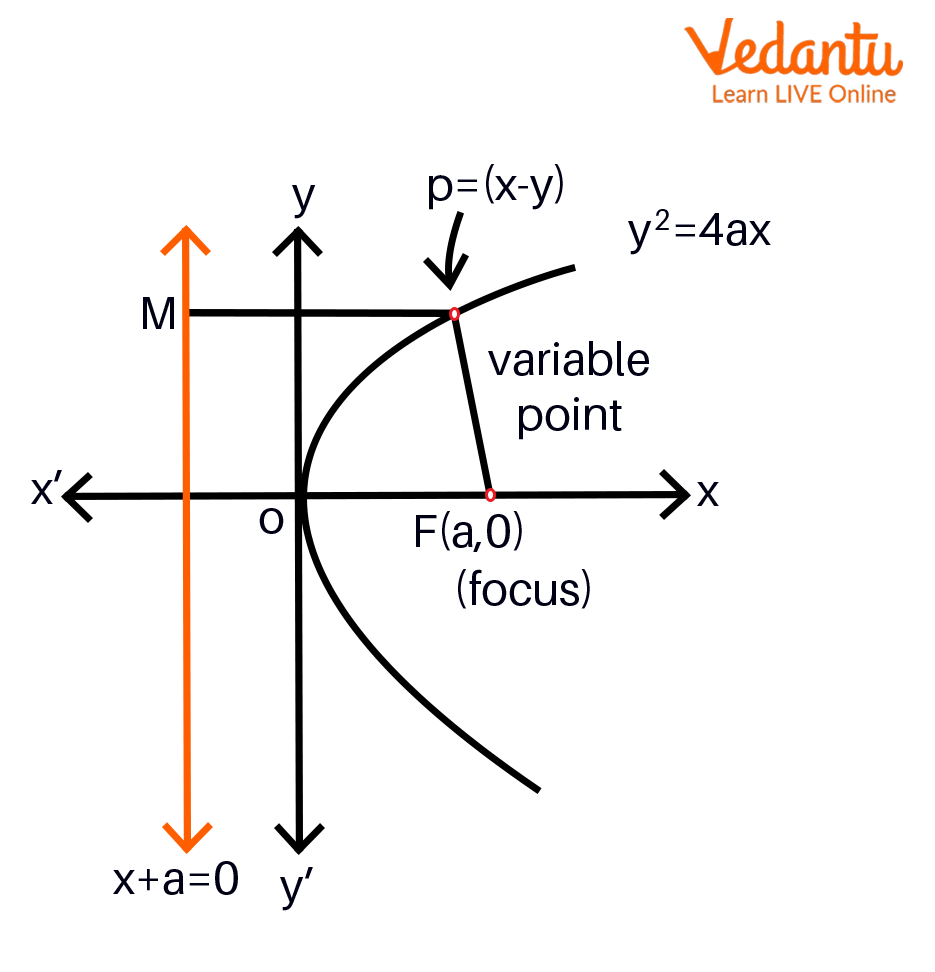
Some of the important terms and parts of a parabola are described here, taking into consideration the standard equation $y^{2}=4ax$.

• Focus: The point $(a, 0)$ is referred to as the parabola's focus, represented by $y^{2}=4ax$.

• Directrix: The line parallel to the y-axis passing through the point $(-a, 0)$ is called the directrix of the parabola represented by $y^{2}=4ax$. The directrix is always perpendicular to the axis of the parabola.

• Focal Chord: The focal chord is the chord of a parabola that passes through the parabola's focus. The focal chord intersects the parabola at two distinct points.

• Focal Distance: The distance of any point $(x_{1},y_{2})$ on the parabola from the focus is called the focal distance. The focal distance is equal to the perpendicular distance of this point on the parabola from the directrix.

• Latus Rectum: It is the focal chord perpendicular to the parabola's axis and passes strictly through the parabola's focus. The length of the latus rectum is evaluated as equal to $4a$. The endpoints of the latus rectum are $(a, 2a)$, and $(a, -2a)$ in this form of a parabola.

• Eccentricity Of Parabola (e = 1): It is the ratio of the distance of any point from the focus, that is the focal distance, to the perpendicular distance of the same point from the directrix. The eccentricity of the parabola is always equal to 1.

Properties of the Parabola

Parabola Formula give us an impression of the general form of the parabolic path in the two-dimensional plane. Some of the note-worthy properties of the parabola are as follows.

Terma Related to a Parabola

• The direction of the parabola is determined by the value of the constant term “a”.

• The coordinates of the vertex of the parabola are $(h,k)$, where $h = -b/2a$ and $k = f(h)$.

• The length of the Latus Rectum of the parabola is $= 4a$.

• The focus of the parabola is referred to by the coordinates $(h, k+ (1/4a))$

• The equation of the Directrix of the parabola is $y = k - 1/4a$

• The eccentricity of the parabola is always 1.

• The parabola is always symmetric about its axis.

• The axis and directrix are perpendicular to each other.

• The axis passes through the vertex and the focus of the parabola.

• The tangent at the vertex of the parabola is always parallel to the directrix.

• The vertex is the midpoint of these two points - focus and the point of intersection of the directrix and the axis.

Graph of Parabola

As we have discussed, the parabola is a U-shaped curve drawn for a quadratic function, $f(x) = ax^{2} + bx + c$. The graph of the parabola will be downward (or we can say opens down), when the value of a is -ve. The parabola graph is upward (or opens up) when the value of a is +ve.

Graph of Parabola

Here we are the universally accepted notion for the positive direction of the XY plane, and so the parabola opens up.

The following are its important parameters.

• Vertex is $(h,k)$

• We get $h = -b/2a$

• Thus vertex becomes $(-b/2a , f(-b/2a))$

• Again, we get $k=f(h)$

• The length of the Latus Rectum $= 4a$

• The focus of the parabola is $(h, k+ 1/4a)$

Area Under the Parabola

The axis of the parabola divides the parabola into two symmetric parts. The area under the parabola is calculated in the following steps.

• Here we take a parabola that is symmetric along the x-axis and has an equation $y^{2}=4ax $.

• This equation is simplified as $y=\sqrt{4ax}$.

• We will first find the area of the parabola in the first quadrant with respect to the x-axis along the limits from 0 to a.

• Now, we integrate the equation to get an answer.

• Then we double the value of the integrated area which offers the area of the whole parabola.

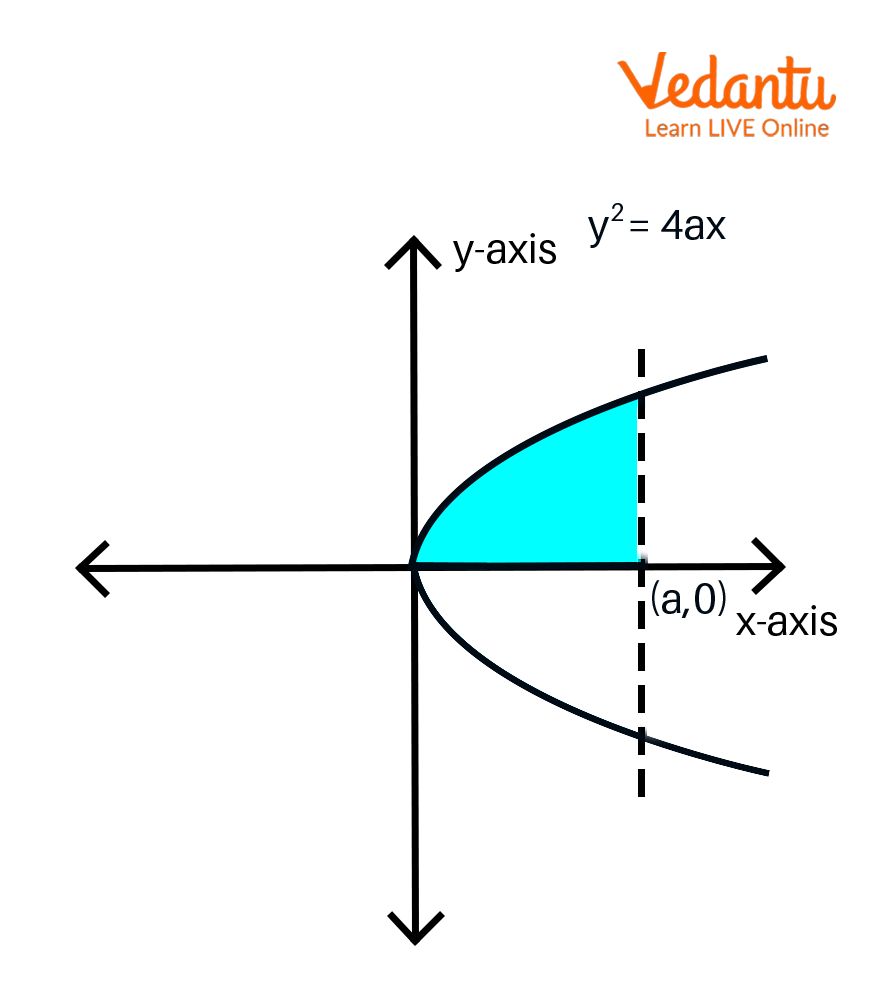
Area Under the Curve

The calculations for deriving the area of the parabola are as follows.

AREA

= $2\int_{0}^{a}\sqrt{4ax}.dx$

$= 4\sqrt{a}\int_{0}^{a}\sqrt{x}.dx$

$=4\sqrt{a}\int_{0}^{a}{{{x}^{\dfrac{1}{2}}}.dx}$

$=4\sqrt{a}\times \left[ \dfrac{{{x}^{\left( \dfrac{1}{2}+1 \right)}}}{\dfrac{1}{2}+1} \right]_{0}^{a}$

$=4\sqrt{a}\times \left[ \dfrac{{{x}^{\dfrac{3}{2}}}}{\dfrac{3}{2}} \right]_{0}^{a}$

$=4\times {{a}^{\dfrac{1}{2}}}\times \dfrac{2}{3}\left[ {{x}^{\dfrac{3}{2}}} \right]_{0}^{a}$

$=4\times {{a}^{\dfrac{1}{2}}}\times \dfrac{2}{3}{{a}^{\dfrac{3}{2}}}$

$=\dfrac{8}{3}{{a}^{2}}$

Therefore, the area of the parabola is $=\dfrac{8a^{2}}{3}$

Interesting facts

• The perimeter of the base of the double right circular cone from which the parabola is formed is called the Directrix.

• The Parabola is symmetric about its axis, and its Vertex is where the parabola intersects its axis of symmetry.

• The Vertex of the parabola is equidistant from its focus and its directrix.

• The Focus of the parabola does not lie on its directrix.

Solved Examples

1. The equation of a parabola is given as $y^{2}=16x$. Find the length of the latus rectum, focus, and vertex of the given parabola.

To find: Length of the latus rectum, focus, and vertex of the parabola

Given: Equation of a parabola is $y^{2}=16x$

Then we get the following

$4a = 16$

$a = 4$

Length of the Latus rectum

$= 4a$

$= 4 \times 4$

$= 16$

Now, the coordinates of the focus $= (a,0) = (4,0)$

Now, the coordinates of the vertex $= (0,0)$

2. Which equation represents a parabola that has a focus at point $(0, 0)$ and the directrix of the parabola is $y = 2$?

Given that the focus is given by the coordinates $(0, 0)$ and the directrix is $y = 2$.

Let us take a point $(x, y)$ on the parabola.

Its distance from the focus point $(0, 0)$ is $(x-0)^{2}+(y-0)^{2}$

Its distance from directrix $y = 2$ is $\left | y-2 \right |$

Therefore, the equation will be as follows

$(x-0)^{2}+(y-0)^{2} = \left | y-2 \right |$

Squaring on both sides.

$(x-0)^{2}+(y-0)^{2} = (y-2)^{2}$

${{x}^{2}}+{{y}^{2}}={{y}^{2}}-4y+4$

$x^{2} + 4y - 4 = 0$

Hence, the equation of the parabola with a focus at $(0, 0)$ and a directrix of $y = 2$ is

$x^{2}+ 4y - 4 = 0.$

Summary

• The parabola has an eccentricity equal to 1.

• The axis and directrix of the parabola are perpendicular to each other.

• The parabola's axis passes through the focus and the vertex of the parabola.

• The only tangent of the parabola parallel to its directrix is the one at its vertex.

• The vertex is the midpoint of these two points - focus and the point of intersection of the directrix and the axis.

Practice Problems

1. Find the equation representing a parabola that has a focus at point $(10, 15)$, and the directrix of the parabola is $y = 12$.

2. Find the vertex of the given parabola $y^{2}-4y=64x$.

3. Find the length of the latus rectum and the focus of the given parabola $y^{2}=256x$.