Perpendicular Bisector And Angle Bisector Theorem Definition Formula Proof And Solved Examples
We come to encounter a variety of shapes in geometry. Among them is a triangle. To address issues involving triangles, we have various theorems at our disposal. Perpendicular bisector and angle bisector theorem are two examples. These crucial triangle theorems will be covered in this essay. A line known as a bisector divides an angle or a line into two parts of equal size. The midpoint of a segment is always contained in the segment's bisector. The perpendicular bisector theorem will be discussed first.
What is a Perpendicular Bisector?
A line segment that crosses another line segment at a right angle and splits that another line into two equal portions at its middle is known as a perpendicular bisector.
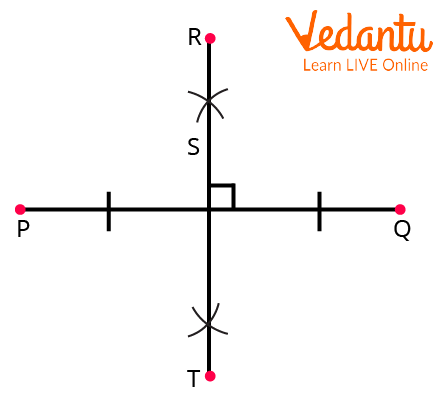
Perpendicular Bisector
What is the Perpendicular Bisector Theorem?
According to the perpendicular bisector theorem, every point on the perpendicular bisector is equally spaced from both of the line segment's endpoints.
Perpendicular Bisector Theorem
In the above figure,
\[\begin{array}{l}MT\; = \;NT\;\;\\MS\; = \;NS\;\;\\MR\; = \;NR\;\;\\MQ\; = \;NQ\end{array}\]
Perpendicular Bisector Theorem Proof
Take a look at the diagram below, where C is just a random point on AB's perpendicular bisector (which intersects AB at D):
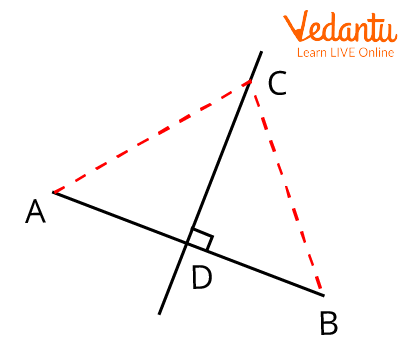
Perpendicular Bisector Proof
Compare the $\triangle ACD$ and $\triangle BCD$.
\[\begin{array}{l}AD = BD\\CD = CD(common)\\\angle ADC = \angle BDC = {90^ \circ }\end{array}\]
By the SAS rule of congruence, the triangle ACD and triangle BCD are congruent.
Hence proved.
What is Angle Bisector Theorem?
According to the Angle Bisector Theorem, the angle bisector of a triangle divides the other side in such a way that the ratio of the two line segments is equal to the ratio of the other two sides. Due to the angle bisector, the lengths of the other two triangle sides are equal to the relative lengths of the opposite side. All varieties of triangles can be analysed using the angle bisector theorem.
Angle Bisector Theorem Statement
The angle bisector theorem states that a triangle's angle bisector separates its opposite side into two pieces that are proportional to its other two sides.
Angle Bisector Theorem Proof
Angle Bisector Theorem Proof
By utilising trigonometry in this case, we can quickly demonstrate the angle bisector theorem. Using the law of sines, we can write the following in the triangles ABD and ACD (in the preceding diagram);
\[\begin{array}{l}\dfrac{{|AB\lvert}}{{|BD\lvert}}\; = \dfrac{{\;\sin \angle BDA}}{{\sin \angle BAD}}\;\;\; \ldots \left( 1 \right)\\\dfrac{{|AC|}}{{|DC|}}\; = \dfrac{{\;\sin \angle ADC}}{{\sin \angle DAC}}\;\;\; \ldots \left( 2 \right)\end{array}\]
Angles ∠ ADC and ∠ BDA are referred to as adjacent supplementary angles since they form a linear pair.
Due to the sine of supplementary angles being equal,
\[\sin \;\angle \;BDA\; = \;\sin \;\angle \;ADC\;\;\;\;\; \ldots ..\left( 3 \right)\]
Also,
\[\angle \;DAC\; = \;\angle \;BAD\;\](Since AD is an angle bisector)
Therefore,
\[\sin \;\angle \;BDA\; = \;\sin \angle \;ADC\;\;\;\; \ldots \left( 4 \right)\]
Since the RHS of equations 1 and 2 are equal, it follows that the LHS will likewise be equally based on equations 3 and 4.
\[\dfrac{{\left| {BD} \right|}}{{\left| {DC} \right|}} = \dfrac{{\left| {AB} \right|}}{{\left| {AC} \right|}}\]
Hence Proved.
Applications of the Perpendicular Bisector and Angle Bisector Theorem
A triangle's lengths can also be determined using the perpendicular bisector theorem in combination with other theorems.
Due to the fact that an angle bisector divides the side opposite the angle into two segments proportional to the triangle's other two sides, the Angle Bisector Theorem aids in determining the lengths of sides of triangles that are unknown.
Interesting Fact
Both angle bisector and perpendicular bisector theorems' converses are true as well.
Solved Examples of the Perpendicular Bisector and Angle Bisector Theorem
1. The perpendicular bisector of triangle ABC on line segment BC in a pyramid is line segment AD. Find the length of side AC if AB is 20 feet long and BD is 7 feet long.
Ans: It is assumed that AD is the line segment's perpendicular bisector on BC.
Therefore, any point on line segment AD is equally far from points B and C according to the perpendicular bisector theorem. Meaning that AB = AC.
Therefore,
\[AC\; = \;20\;feet\]
2. Can we state that the vertex between equal sides in any equilateral or isosceles triangle lies on the perpendicular bisector of the base?
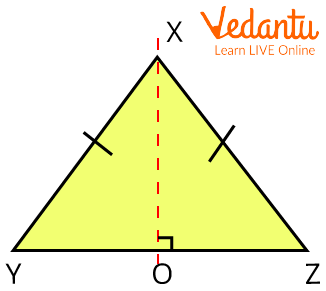
Triangle XYZ
Ans: From vertex X, create a perpendicular that intersects segment YZ at point O.
The inverse of the perpendicular bisector theorem is used to demonstrate that
\[OY = OZ\]
If \[XY\; = \;XZ\].
On the perpendicular bisector of the triangle's base, YZ is where vertex X is located.
3. Using the angle bisector theorem, determine the value of x for the given triangle.
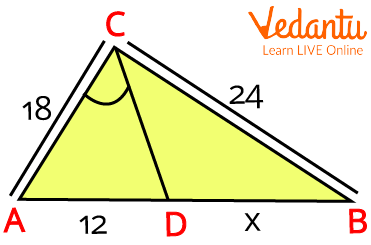
Triangle ABC
Ans: Given data,
$AD=12$, $AC=18$, $BC=24$, and $DB=X$.
By the angle bisector theorem,
\[\dfrac{{AD\;}}{{AC}} = \dfrac{{\;DB}}{{BC}}\]
Now replace the values, we get
\[\begin{array}{l}\dfrac{{12}}{{18}} = \dfrac{{\;X\;}}{{24}}\\X = \dfrac{{\;2\;}}{3}\left( {24} \right)\\X = \;2\left( 8 \right)\;\\X = \;16\end{array}\]
Therefore, the value of X is 16.
Important Points to Remember
The SAS congruence criterion can be used to demonstrate the perpendicular bisector theorem and its opposite.
In order to create something in the middle and an equal distance from each endpoint, the perpendicular bisector theorem is employed in the construction of buildings, bridges, and other structures.
Important Formulas from the Theorem
According to the perpendicular bisector theorem, if a bisector CD bisects the triangle ABC in two triangles, then
$\angle ADC = \angle BDC = {90^ \circ }$
According to the angle bisector theorem, for a triangle ABC having a bisector AD
\[\dfrac{{\left| {BD} \right|}}{{\left| {DC} \right|}} = \dfrac{{\left| {AB} \right|}}{{\left| {AC} \right|}}\]
Conclusion
The perpendicular bisector and angle bisector theorems and their explanations have been covered in-depth in this article. We may infer from the examination of these two theorems above that each of them is important to Mathematics and has a variety of implications. The theorems hold valid similarly.
FAQs on Perpendicular Bisector And Angle Bisector Theorem in Geometry
1. What is the perpendicular bisector in geometry?
The perpendicular bisector of a line segment is a line that divides the segment into two equal parts at a 90° angle. It has two key properties:
- It passes through the midpoint of the segment.
- It forms a right angle (90°) with the segment.
2. What is the perpendicular bisector theorem?
The Perpendicular Bisector Theorem states that any point on the perpendicular bisector of a segment is equidistant from the segment’s endpoints. If a point P lies on the perpendicular bisector of AB, then PA = PB. This theorem is commonly used to prove triangle congruence and solve distance problems.
3. What is the angle bisector theorem?
The Angle Bisector Theorem states that in a triangle, the angle bisector divides the opposite side in the ratio of the other two sides. In triangle ABC, if AD bisects ∠A and meets BC at D, then BD/DC = AB/AC. This theorem helps in finding unknown side lengths in triangles.
4. How do you construct a perpendicular bisector of a line segment?
To construct a perpendicular bisector, follow these steps:
- Draw a line segment AB.
- With a compass radius greater than half of AB, draw arcs above and below the segment from point A.
- Without changing the radius, draw arcs from point B to intersect the previous arcs.
- Join the intersection points of the arcs.
5. How do you use the angle bisector theorem to find a missing side?
To use the Angle Bisector Theorem, set up a proportion using side ratios. For example, in triangle ABC, if AD bisects ∠A and BD = 3 cm, DC = 2 cm, and AB = 6 cm, then:
- BD/DC = AB/AC
- 3/2 = 6/AC
6. What is the difference between a perpendicular bisector and an angle bisector?
The perpendicular bisector divides a line segment into two equal parts at 90°, while the angle bisector divides an angle into two equal angles. Key differences:
- Perpendicular bisector works on line segments.
- Angle bisector works on angles in triangles.
- Perpendicular bisector creates equal distances to endpoints.
- Angle bisector creates proportional side segments.
7. Why are points on a perpendicular bisector equidistant from the endpoints?
Points on a perpendicular bisector are equidistant from the endpoints because they form two congruent right triangles. If P lies on the perpendicular bisector of AB, then triangles PAA' and PBB' share:
- Equal halves of AB
- A right angle
- A common side
8. Does every triangle have angle bisectors and perpendicular bisectors?
Yes, every triangle has three angle bisectors and three perpendicular bisectors. Important points formed are:
- The angle bisectors meet at the incenter.
- The perpendicular bisectors meet at the circumcenter.
9. What is the formula for the angle bisector theorem?
The formula for the Angle Bisector Theorem is BD/DC = AB/AC in triangle ABC when AD bisects ∠A. This means the opposite side is divided in the same ratio as the adjacent sides. It can be rearranged to solve for unknown lengths using cross-multiplication.
10. What are common mistakes when using the perpendicular and angle bisector theorems?
Common mistakes include mixing up properties of the perpendicular bisector and the angle bisector. Frequent errors are:
- Assuming an angle bisector creates equal sides instead of a ratio.
- Forgetting the 90° condition in a perpendicular bisector.
- Writing the angle bisector ratio incorrectly (wrong order).
- Not checking that the point actually lies on the bisector.
