




How to Find the Perimeter Using Diagrams: Step-by-Step Method
Let's imagine that you have a rectangular yard, and you want to fence it to protect it from street animals and you also want to decorate it with beautiful grass and flowers. So now you need to calculate its area and perimeter. After reading this question, you might wonder what is the perimeter and area of a rectangle. Here, we will learn about it by using examples of the perimeter and area of a rectangle. We will complete all this learning, keeping in mind the geometrical properties of a rectangle. So let's get started.
What is a Rectangle with a Rectangle Diagram?
The rectangle is a closed quadrilateral, having four sides and four angles. The opposite sides of a rectangle are equal and parallel to each other. All the angles are equal and of $90^{\circ}$. The rectangle diagram is given below:
Rectangle diagram
Geometrical Properties of a Rectangle
A rectangle is a quadrilateral.
The opposite sides are parallel and equal to each other.
Each interior angle is equal to $90^{\circ}$.
The sum of all the interior angles is $360^{\circ}$.
The diagonals bisect each other.
The Perimeter of a Rectangle
The perimeter of any shape is the total distance around its sides. It is defined as the length of the boundary or the outline of any shape. Remember one thing, perimeter changes as the shape and measure of the dimensions change.
The perimeter of a rectangle is defined as the total distance around the rectangle. For example, Let's imagine that there is a rectangle which is made with wire whose length is l. The same wire can be reused to make a triangle. Considering that all sides are equal in length. The perimeter diagram is given below:
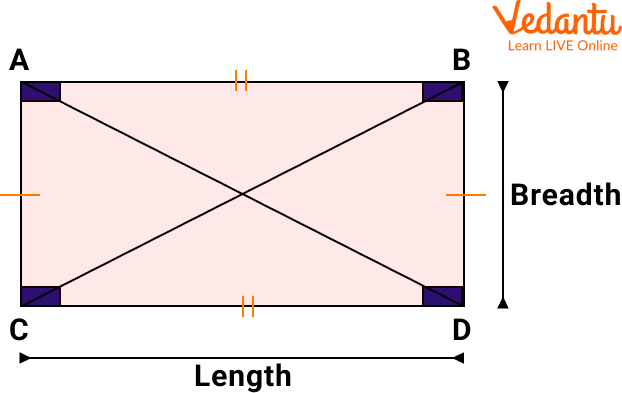
Perimeter Diagram
Rather than adding every side, we have some formula for calculating the perimeter of a rectangle. As the opposite sides of a rectangle are equal, its perimeter is given by length + breadth + length + breadth, which implies 2 (length + breadth). Thus, the formula to calculate the perimeter of the rectangle is:
$\mathrm{P}=2 \times(\mathrm{l}+\mathrm{b})$, where $\mathrm{I}$ is the length and $\mathrm{b}$ is the breadth of the rectangle.
Area of a Rectangle
The area of any shape can be defined as the space required by it to fit the number of square units. The area of a rectangle is defined as the space occupied by it. It is calculated by using the dimensions of the rectangle. The area of a rectangle is given as the product of its length and breadth, i.e.
$A=L \times B$, where $L$ refers to the length and $B$ refers to the breadth of a rectangle.
Application of the Perimeter and the Area in Daily Life
We need an area to calculate how much carpet is used to cover the floor.
We need a perimeter to calculate how much wire is required for the fencing.
While making swimming pools we need both perimeter and area to know the required dimension will fit in the area or not.
In farming, we use the area to calculate how much grain we can grow on the given land.
Solved Examples of the Perimeter and Area of a Rectangle
Q1. Find the perimeter of the figure shown below.

Perimeter Diagram
Ans: The above figure shows that the rectangle is 9 inches in length and 3 inches in breadth. Here, $\mathrm{I}=9$ and $\mathrm{b}=3$
The perimeter of the rectangle $=2(l+b)$
$=2(3+9)$
$=2(12)$
$=24 \text { inches }$
Therefore, the perimeter of a rectangle is 24 inches.
Q2. Find the area of the figure which is given below.

Rectangle Diagram
Ans: The above figure shows that the rectangle has a $5 \mathrm{~cm}$ length and $4 \mathrm{~cm}$ breadth.
Here, $l=5$ and $b=4$
Area of rectangle $=$ length $x$ breadth
$=5 \times 4$
$=20 \mathrm{~cm}^2$
Therefore, the area of a rectangle is $20 \mathrm{~cm}^2$.
Practice Questions
Q1. Find the perimeter and area of the rectangle of length 17 cm and a breadth of 13 cm.
Ans: Perimeter $=60 \mathrm{~cm}$
Area $=221 \mathrm{~cm}^2$
Q2. Find the perimeter of a rectangle whose length and width are 20 cm and 9 cm respectively.
Ans: Perimeter = 58 cm
Q3. A rectangular yard has a length equal to 10 cm and a perimeter equal to 60 cm. Find its width.
Ans: Width = 20 cm
Summary
So in this article, we have learned about the perimeter and area of a rectangle in a very enjoyable and learnable way. We learned that it only sounds tricky but it becomes very easy if paid a little attention. In this article, we have learned about the definitions of rectangle, perimeter, and area, along with the rectangle diagram and the perimeter diagram. We also studied the formula to calculate the area and perimeter of a rectangle, using some examples and practice problems.
FAQs on Perimeter Diagram: Definition, Formula & Solved Examples
1. What is the basic definition of a perimeter in geometry?
In geometry, the perimeter is defined as the total length of the boundary of a closed, two-dimensional shape. Imagine walking along the edge of a park; the total distance you cover to return to your starting point is its perimeter. It is a one-dimensional measurement, typically expressed in units like centimetres (cm) or metres (m).
2. What are the formulas for calculating the perimeter of a square and a rectangle?
Calculating the perimeter for common shapes involves simple formulas:
- For a square: Since all four sides are equal, the formula is P = 4 × side.
- For a rectangle: Since opposite sides are equal, the formula is P = 2 × (length + width).
3. How do you calculate the perimeter of a circle, and what is it called?
The perimeter of a circle has a special name: the circumference. It is calculated using the formula C = 2πr, where 'C' is the circumference, 'r' is the radius of the circle, and π (pi) is a mathematical constant approximately equal to 3.14159.
4. How is the concept of perimeter used in real-life examples?
Understanding perimeter is crucial for many practical tasks. For example, you would need to calculate the perimeter to:
- Determine the amount of fencing needed to enclose a garden or a yard.
- Measure the length of a decorative border for a room or a picture frame.
- Calculate the total distance of one lap around a running track or a sports field.
5. What is the fundamental difference between perimeter and area?
The main difference lies in what is being measured. Perimeter measures the length of the outer boundary of a shape (a linear distance). In contrast, area measures the total amount of surface or space enclosed within that boundary. For instance, the perimeter of a field is the length of its fence (measured in metres), while the area is the amount of grass inside the fence (measured in square metres).
6. How can you find the perimeter of an irregular polygon?
For an irregular polygon (a shape with straight sides of different lengths), there is no special formula. To find the perimeter, you simply add together the lengths of all its individual sides. This method works for any closed shape with straight edges, regardless of how many sides it has.
7. Is it possible for two different shapes to have the same perimeter but different areas?
Yes, it is entirely possible. This highlights the key difference between the two measurements. For example, a rectangle with a length of 9 cm and a width of 3 cm has a perimeter of 24 cm and an area of 27 cm². A square with sides of 6 cm also has a perimeter of 24 cm, but its area is 36 cm². Both have the same boundary length but enclose different amounts of space.

















