An Introduction to Circle
A circle is a two-dimensional shape made up of points that are stretched out from a given point (centre) on the plane by a fixed or constant distance (radius). The fixed point is referred to as the circle's origin or centre, and the fixed distance between each point and the origin is referred to as the radius. Calculating the perimeter and area of a circle is one of the earliest ways to learn how to work with pi. Find out how to calculate these measurements in this article that breaks down the formulas used for calculating these values.
A circle
What is the Perimeter of a Circle?
The boundary or overall arc length of a circle's perimeter is known as its perimeter. A circle's circumference is the term used to describe its edge. Therefore, since the perimeter of a circle provides information on its circumference, the formula is also referred to as the circumference of a circle.
The Perimeter of Circle Formula
The circle's radius acts as one of the three variables in the perimeter of a circle formula, along with two constants.
Perimeter of a circle $=2 \pi r=\pi d$ units
Here,
$r=$ radius of the circle
$d=$ diameter of the circle
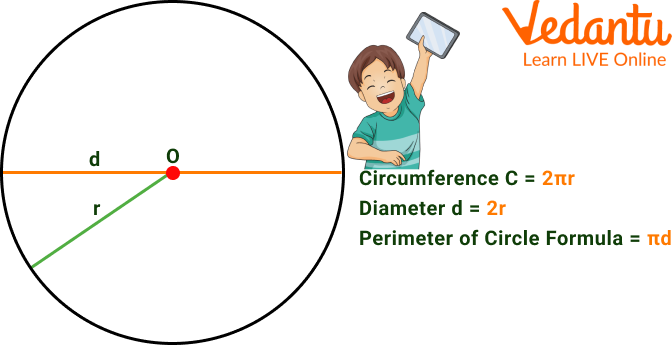
Perimeter of Circle Formula
How to Find the Area of the Circle?
The area of a circle is the space occupied by the circle in a two-dimensional plane. Alternatively, the space occupied within the boundary/circumference of a circle is called the area of the circle.
The circle area formula is $A=\pi r^2$.
To calculate the area of the circle, we must know its radius or its diameter. It is calculated by multiplying $\pi$ by the radius squared: $A=\pi r^2$
Here, r is the radius of the circle.
We can also calculate the area of a circle based on its diameter.
We already know that the radius can be expressed as the diameter divided by two:
$D=2 r$
$r=\dfrac{D}{2}$
If we substitute this expression for the radius in the formula for the area of the circle, we obtain the formula as a function of the diameter:
$A=\pi\left(\dfrac{D}{2}\right)^2$
$A=\pi\left(\dfrac{D^2}{4}\right)$
Where $D$ is the diameter of the circle.
Circle Area Formula
The image below shows the area of the circle formula, with $r$ as the radius and $d$ as the diameter.
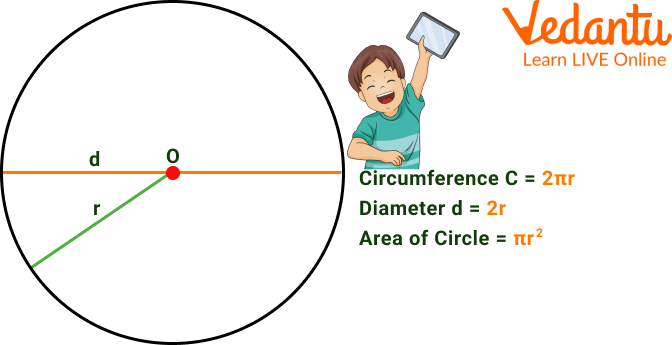
Circle Area Formula
Solved Examples
Q 1. What is the area of a circular park with a diameter of 8 feet?
Ans: Given that the diameter of the circular park is 8 feet.
Thus, the radius of the park is half the diameter. That is, the radius is 4 feet. Use the formula for the area of a circle, $A=\pi r^2$, where $r$ is the circle's radius. Substitute 4 for $r$ in the formula.
$A=\pi(4)^2$
$A=\pi(16)$
$A=3.14(16)$
$A=50.24 f t^2$
Therefore, the park's area is $50.24 \mathrm{ft}^2$.
Q 2. What is the perimeter of a circle pizza if the area is $25 \mathrm{~cm}^2$?
Ans: The circle area formula is:
$A=\pi r^2$
We substitute the area for the value of $25 \mathrm{~cm}^2$ that gives us the statement:
$25=\pi r^2$
Then we isolate $r$ and operate to obtain its value:
$r =\sqrt{\dfrac{25}{\pi}}$
$r =\sqrt{7.95}$
$r =2.82 \mathrm{~cm}$
Put the value in the perimeter of the circle formula:
$P=2 \pi r$
We substitute the value of the radius in the circumference of a circle formula:
$P=2 \pi(2.82)$
$P=2(3.14)(2.82)$
$P=17.71 \mathrm{~cm}$
The circle's perimeter is $17.71 \mathrm{~cm}$.
Practice Questions
Q 1: What is the perimeter of a circle knowing its diameter is 2m?
Ans: 6.28 m
Q 2: Find the area of a circle with a radius of 20 cm.
Ans: $1256.63 \mathrm{~cm}^2$
Summary
We discussed here in the article the perimeter and area of a circle. The space a circle takes up on a two-dimensional plane is known as the area of the circle. Alternately, the area of the circle is the area included inside the circumference or perimeter of the circle. $A=\pi r^2$, where $r$ is the circle's radius, is the formula for calculating a circle's surface area.
The length of the circle's edge determines its circumference. This implies that a circle's circumference and perimeter are equal. The circle's circumference will equal the length of the rope that precisely encircles its edge.
FAQs on Perimeter and Area of Circle
1. What are the major parts of a circle?
The list of the different circle parts includes tangent, chord, radius, diameter, minor arc, major arc, minor segment, major segment, minor sector, and major sector.
2. What is a half-circle called in geometry?
Half of a circle is called a semicircle in geometry. The circle is divided into two equally sized semi circles by diameter.
3. What are the properties of the circle?
Properties of a circle:
Congruent circles have equal radii.
The circles with various radii also seem to be similar to one another.
The length of the chords that are equally spaced from the centre is the same.
The circle's points are evenly spaced apart from one another.
The diameter is the circle's longest chord.
A circle's diameter splits it into two equal arcs. The arcs are all semicircles.
Two circles are congruent if their radii exactly match each other's values.
Concentric circles are two or more circles with various radii and a common centre.
