Fraction to Percent

Introduction

In our day to day life, many a time we compare two quantities. We generally use fractions and percent for the comparison. The fraction refers to how many parts of a given whole quantity. While, percentage or percent refers to how many parts out of 100 quantities.

What is Fraction?

The term fraction represents how many parts of a given whole quantity or, in general, it describes how many parts of a certain size divided by the whole quantity.

Fraction consists of Numerator which is written above the line and Denominator which is written below the line.

The numerator indicates a number of equal parts, and the denominator indicates how many of those parts make up a whole. The denominator of a fraction can never be zero because zero parts can never make up a whole.

For example, In the simple fraction \[\frac{1}{2}\], the numerator ‘1’ indicates that the fraction represents 1 equal part, and the denominator ‘2’ indicates that 2 parts make up a whole.

Fraction to Percentage

A fraction can be a portion or any quantity of a whole, which could be any number, a specific value, or a portion itself. Fractions and percentages both represent parts of a whole. To convert a fraction into a percentage, the fraction must be multiplied by 100.

Fractions are represented as numerical values that define parts of a whole. For example, half of a total is represented as $\dfrac{1}{2}$ in fractional form. Fractions consist of a numerator (the number on the top) and a denominator (the number on the bottom).

Fraction to Percentage Conversion

What is Percent?

The term percent represents how many parts out of 100 quantities. In other words, Percentages are the numerators of the fractions with denominator 100.

The word ‘Percent’ has been derived from Latin word ‘per centum’ which means ‘per hundred’.

The percentage is a dimensionless pure number.

The percent is denoted using the sign % meaning hundredths.

For example, 5% means 5 out of one hundred or Five hundredth.

It can be written as: \[5\% = \frac{5}{{100}} = 0.05\]

Percentage Formula

Percentage formula is used to find the share or amount of something in terms of 100.

The Percentage Formula is given by:

Percentage =\[\frac{{{\text{Given value}}}}{{{\text{Total value}}}} \times \] 100

How to Convert a Percentage into a Number?

The percentage formula is used to find the share of a whole in terms of 100. Using this formula, you can represent a number as a fraction of 100. If you observe carefully, all the three ways to get percentage shown above can be easily calculated by using the formula given below:

Percentage= (Value/Total Value)×100

How Fractions and Percentages are Used for Comparing Two Quantities?

To understand this let us consider an example, In the annual exam reports of two friends Henna and Mona, Henna got 320 marks out of 400 i.e. \[\frac{{320}}{{400}}\]and her friend Mona got 350 marks out of 500 i.e. \[\frac{{350}}{{500}}\]. If we compare the marks obtained by them then Mona has secured more marks than Henna. But, only by seeing their obtained marks, we cannot decide who has performed better in their annual exam because the maximum marks out of which they got the marks are not the same. For this, we have to convert their obtained marks given in fraction to their equivalent percentage.

How to Convert Fraction to Percent?

The following steps are followed to convert fraction to percent:

Step 1: Convert the given fraction into its equivalent decimal number (refer Note).

Step 2: The obtained decimal number is multiplied by 100, to get the required percent value.

Note: Fractions are converted to their equivalent decimal number using the following steps:

Step 1: The numerator of fraction is divided by its denominator.

Step 2: The quotient obtained after division is the decimal equivalent of a given fraction.

Solved Examples

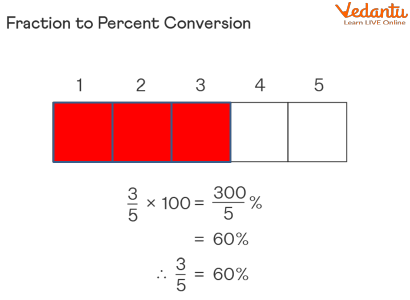
Q.1. Convert the fraction \[\frac{2}{5}\] to a percent.

Solution:

Step 1: Convert the given fraction\[\frac{2}{5}\] into its equivalent decimal number. i.e.

⇒ \[\frac{2}{5}\]= 0.4

Step 2: Multiply the obtained decimal by 100. i.e.

⇒ 0.4 \[ \times \]100 = 40%

Therefore, the required percent value of fraction \[\frac{2}{5}\] is 40%

Q.2. Out of 40 students in a class, 8 are absent. What percent of the students are absent?

Solution: Given, total number of students in class = 40. And, Number of absent students = 8.

Therefore, percentage of absent students in the class = \[\frac{8}{{40}}\]\[ \times \]100 = 20%

Q.3. In the annual exam reports of two friends Henna and Mona, Henna got 320 marks out of 400 and her friend Mona got 350 marks out of 500. Who has performed better?

Solution: First we will convert their obtained marks into its percentage equivalent.

Therefore, percentage of marks obtained by Henna = \[\frac{{320}}{{400}} \times \]100 = 80%

And percentage of marks obtained by Mona = \[\frac{{350}}{{500}} \times \] 100 = 70%

On comparing their percentage of marks obtained, Henna has performed better than Mona.

Q.4. An alloy contains 33% aluminium. What quantity of alloy is required to get 132 g of aluminium?

Solution:

Let the quantity of alloy required be x g

Then 33 % of x = 132 g

⇒ \[\frac{{33}}{{100}} \times X = 132g\]

⇒ \[X = \frac{{132 \times 100}}{{33}}g\]

⇒ x = 400 g

Therefore, the amount of alloy required to get 132 g of aluminium is 400 g.

Tips and Tricks

1. If the denominator of the fraction is 100, then you can simply put the numerator as the solution. Just remove the denominator from the fraction and add a % symbol.

2. If the denominator is not 100 but a number like 25 or 50 or 10, which when multiplied by a minor or simple number will give 100 as a product, the process can be simpler.

Multiply the entire fraction with the whole number, which, when multiplied by the denominator, gives the product 100.

Since the denominator is 100, the numerator can be written with a % sign.

• For example, when converting $\dfrac{9}{25}$ into a percentage:

$\dfrac{9}{25} \times \dfrac{4}{4}=\dfrac{36}{100}$

$\dfrac{36}{100}=36 \%$

Thus, the percentage form becomes 36%

You can also simply divide the numerator and the denominator and then multiply the quotient with 100.

Summary

Fractions represent parts of a whole. Percentages refer to a number or ratio that can be represented as a fraction of 100. Thus, essentially percentages and fractions both represent a certain division of an object or number. To convert a fraction into a percentage, the numerator must be multiplied by 100, and then the new numerator (product of the old numerator and 100) must be divided by the denominator. The quotient found becomes the percentage form of the fraction.