What is Division?

Kids, I hope you have seen your teacher distribute chocolates among your friends so everyone gets the same amount of chocolates. Do you wonder how they know how many chocolates each student should get so that every student can get an equal amount of chocolates? Yes, it is done using division.

Division breaks down a large group into smaller parts. Division can also be separated into two parts, areas, or groups. Every arithmetic operation has its unique symbol. In division, the sign is ‘÷’ or ‘/’ or ‘_’.

For example, we can write,

$\begin{array}{l}20 \div 5 = 4\\\dfrac{{20}}{5} = 4\end{array}$

A decimal point will be added if a smaller value is divided by a larger one. The division is the opposite of multiplication.

What is the Maths Division?

There are four basic arithmetic operations, i.e., addition, subtraction, multiplication, and division. Today, we will discuss division or, to be more precise, 20 divisions. It is when more significant numbers are broken down into smaller groups keeping the number of items constant. In division, there are four main parts.

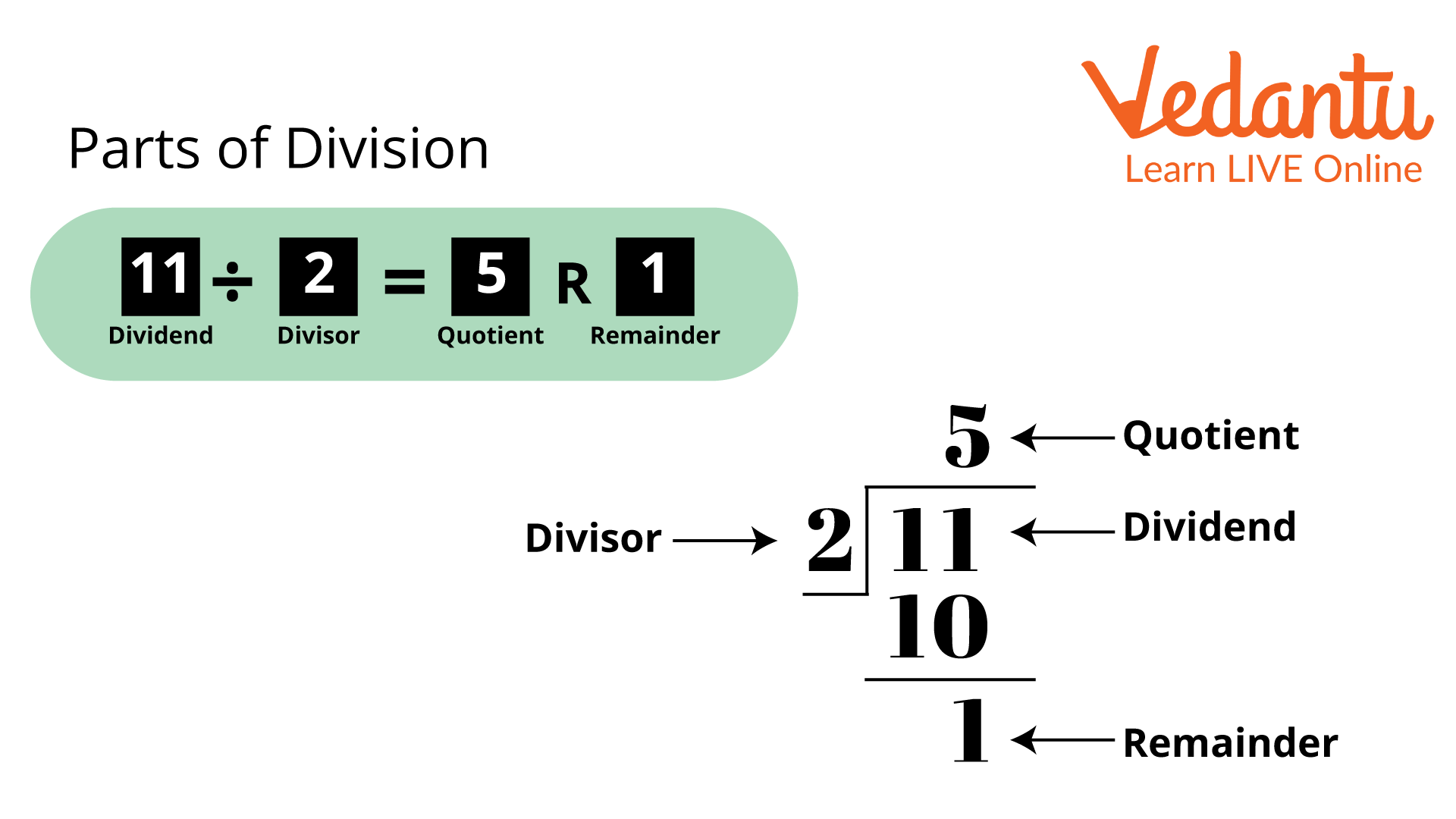
Parts of Division

In this image, as you can see, 11 is divided by 2.

11 is the dividend, 2 is the divisor, 5 is the quotient, and 1 is the remainder.

Formulas to Solve Division

To solve division sums, we need to follow a fundamental yet important formula given below:

∴ $Dividend{\rm{ }} = {\rm{ }}\left( {Divisor{\rm{ }} \times {\rm{ }}Quotient} \right){\rm{ }} + {\rm{ }}Remainder$

This general formula is known as the division formula.

The formula allows us to check the values of the remainder and quotient after division. In the given equation, we can change the quotient, remainder, and divisor values to see if the result and the dividend are the same or fix it otherwise.

How to Solve Division Sums?

Now we will learn how to solve division sum practically.

However, to get a clear view, let us take an example where we will divide 75 by 5.

• First, we need to draw the division symbol $\left){\vphantom{1{}}}\right.\!\!\!\!\overline{\,\,\,\vphantom 1{{}}}$ and write the divisor, in this case, it is 5 on the left side, and the dividend is 75 inside the division symbol.

• Now take the first digit of the dividend from the left, i.e., 7 and check that number is greater than or equal to the divisor. If it is less than the divisor, then the first two digits of the dividend are considered.

• After that, divide it by the divisor, then write the result as the quotient on top. In this case, the quotient of $7 \div 5$ is 1.

• Now, subtract the result of the divisor and the quotient's written digit.

• Subtract $\left( {5 \times 1} \right)$ from the dividend's first digit, then enter the results. In this case, the difference is 7 - 5 = 2.

• Now, if present, we have to write down the next digit of the dividend. The following number is 5.

• Repeat the same process until the remainder is less than the divisor.

• In division, generally, its quotient is considered as the result.

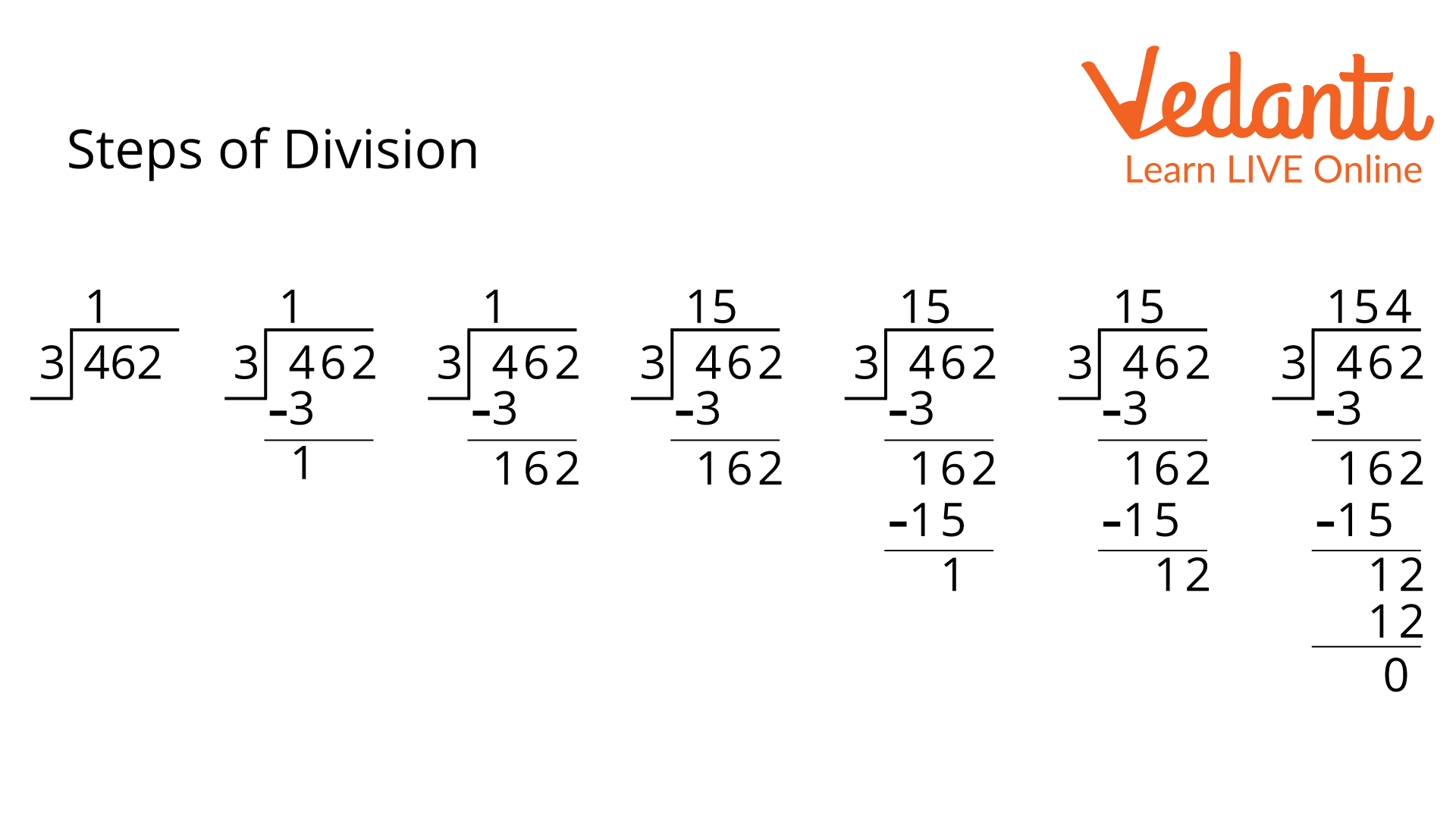
Steps of Division

Division of 20

According to a few basic division rules, one’s digit of 20 is 0. Then it can conclude that it is always divisible by 2 and 5. The divisibility rule of 2 states that if one’s place digit is even, then the number is divisible by 2. Here, the number is 20 and its unit place is 0, so 20 is divisible by 2. And the divisibility rule of 5 states that if the unit place of the number is 0 or 5, then it is divisible by 5. So, here 0 is at the unit place of 20, so, it is divisible by 5.

Division Examples with Answers

For a better understanding of division, let's look at a few examples to understand division better.

Example 1:

Perform the division: 121 and 11.

Solution:

According to question $121 \div 11$.

In the given question, we must know the multiplication table of 11.

Now using the multiplication table, $121 \div 11 = 11$.

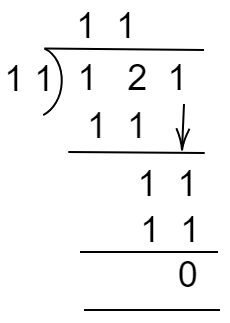
Steps of $121 \div 11$

Therefore, the quotient is 11.

Example 2:

Perform the division: 400 and 20.

Solution:

According to the question, $400{\rm{ }} \div {\rm{ }}20$.

To solve the given question, we must know the multiplication table of 20.

Now using the multiplication table, $400{\rm{ }} \div {\rm{ }}20$.

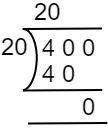
Steps of $400{\rm{ }} \div {\rm{ }}20$

Therefore, the quotient is 20. Example 3:

How many chocolates will each of the kids get if Ria has 20 kids and she buys 80 chocolates for both of them?

Solution:

According to the question, we know the number of kids = is 20 and the number of chocolates = 80.

Thus, the number of chocolates for each kid $ = {\rm{ }}80{\rm{ }} \div {\rm{ }}20$.

To solve the given question, we must know the multiplication table of 20.

Now using the multiplication table, $80{\rm{ }} \div {\rm{ }}20 = 4$.

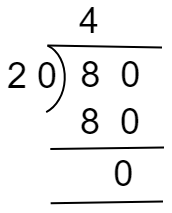
Steps of $80{\rm{ }} \div {\rm{ }}20$

Therefore, the quotient is 4.

Hence, each kid will get 4 chocolates.

Conclusion

After reading the article, it is clear that division requires knowledge of multiplication tables. Working with money is one of the division's most common applications. It can also be used to count everyday items. If we need to divide 10 chocolates between 2 children, we will use the arithmetic process of division.