Courses

Courses for Kids

Free study material

Store

Talk to our experts

1800-120-456-456

Maths

Factors of 156

Factors of 156

Reviewed by:

Rama Sharma

Latest Updates

Explore Now :

JEE Mains 2025 Question Papers

Check Now :

Rank Predictor JEE Main 2025

Predict Now :

Marks Vs Percentile JEE Mains 2025

Factor of 156: An Introduction

The factors of $156$ are the numbers that completely divide $156$ and yield zero as a remainder. In addition, these divisors result in a quotient of whole numbers. These divisors, as well as whole number quotients, are referred to as factors. The factors of number $156$ can be expressed in positive form as well as in negative form. Similarly, the pair factors of the number $156$ can be represented using the positive and negative forms.

What are the Factors of $156$ ?

In Mathematics, the numbers that divide $156$ completely without leaving any remainder are the factors of $156$ . In other words, the factors of $156$ are the numbers multiplied in pairs, resulting in the original number $156$ . Since the product of two negative numbers is a positive number, $156$ has negative and positive factors, but we will use only positive ones.

Let's start by checking for the factors of $156$ . We start with $1$ and check $2, 3, 4, 5, 6, 7$ up to $78$ (half of $78$ ) to see if any numbers can divide $156$ and leave zero as the remainder, then the corresponding divisor and quotient will be treated as the factors of $156$ .

$156 \div 1 = 156$

$156 \div 2 = 78$

$156 \div 3 = 52$

$156 \div 4 = 39$

$156 \div 5 =31.2 (not completely divisible, this is not a factor)

$156 \div 6 = 26$

$156 \div 12 = 13$

$156 \div 13 = 12$

$156 \div 26 = 6$

$156 \div 39 = 4$

$156 \div 52 = 3$

$156 \div 78 = 2$

$156 \div 156 = 1$

Therefore, the Factor of $156$ : $1, 2, 3, 4, 6, 12, 13, 26, 39, 52, 78 $a n d$ 156$(itself).

Negative Factors of $156$

It is possible to have negative factors of 156 in mathematics. Therefore, if we just reverse the positive numbers into their opposites, those negative numbers would likewise be factors of $156 : - 1, - 2, - 3, - 4, - 6, - 12, - 13, - 26, - 39, - 52, - 78$ , and $- 156$

Prime Factor of $156$

A prime number is an integer greater than $1$ whose only factors are $1$ and itself. Prime Factors of $156$ are all the prime numbers that, when multiplied together, equal $156$ .

$156$ is divisible by the prime number $2$ which results in $78$ . The same step can be applied one more time, and the resultant value will be $39$ . Continuing, the number $39$ is divisible by the prime number $3$ , and the result after division will be $13$ . The result $13$ cannot be divided further as it is a prime number.

Hence the prime factors of $156$ are $2, 2, 3, 13$ .

Prime Factorization of $156$

The method used to determine which prime numbers can be multiplied to produce the original number is known as prime factorization. The prime factorization of $156$ is $2 \times 2 \times 3 \times 13$ .

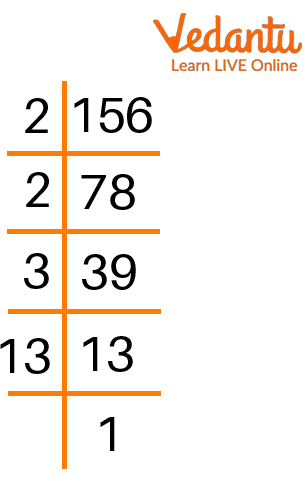
Prime Factorization of 156

Here, $156$ is an even composite number, which can be further divided into its prime factors. Thus, $156$ is written as the product of $12$ and $13$ .

Here, $13$ is a prime number, and $12$ is a composite number that can again be split as $4 \times 3$ and equal to $2 \times 2 \times 3$ .

Thus, $156$ is written as $2 \times 2 \times 3 \times 13$ .

Therefore, the prime factorization of $156$ is $2 \times 2 \times 3 \times 13$ or $2^{2} \times 3 \times 13$ , where $2, 3 a n d 13$ , are prime numbers.

Factor Tree of $156$

The factors of $156$ in tree form are

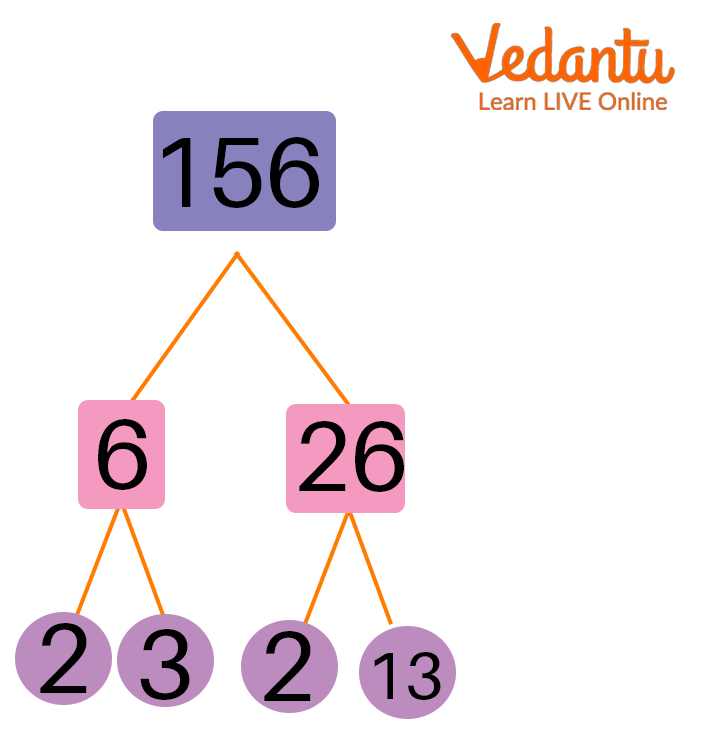
Factor Tree of 156

Pair Factor of $156$

In maths, a factor pair is defined as a set of two factors, which, when multiplied together, give the number.

A factor pair is a combination of two factors that can be multiplied to equal $156$ .

Positive Pair Factors of $156$ :

$1 \times 156 = 156$ ; $(1, 156)$

$2 \times 78 = 156$ ; $(2, 78)$

$3 \times 52 = 156$ ; $(3, 52)$

$4 \times 39 = 156$ ; $(4, 39)$

$6 \times 26 = 156$ ; $(6, 26)$

$12 \times 13 = 156$ ; $(12, 13)$

We can also obtain negative pair factors as the product of two -ve numbers:

$- 1 \times - 156 = 156$ ; $(- 1, - 156)$

$- 2 \times - 78 = 156$ ; $(- 2, - 78)$

$- 3 \times - 52 = 156$ ; $(- 3, - 52)$

$- 4 \times - 39 = 156$ ; $(- 4, - 39)$

$- 6 \times - 26 = 156$ ; $(- 6, - 26)$

$- 12 \times - 13 = 156$ ; $(- 12, - 13)$

Solved Examples

Example 1: Example 2: Calculate the mean of all the factors of $156$ .

Solution: We are aware that factors of $156 = 1, 2, 3, 4, 6, 12, 13, 26, 39, 52, 78 a n d 156$ .

The mean is equal to the total number of terms plus their sum.

$m e a n = \frac{(1 + 2 + 3 + 4 + 6 + 12 + 13 + 26 + 39 + 52 + 78 + 156)}{12} = \frac{392}{12}$

The average of all the $156$ factors is, therefore $32.667$ .

Example 2: Is $1$ the greatest common factor (G.C.F) of $156$ and $165$ ?

Solution: Factors of $156 = 1, 2, 3, 4, 6, 12, 13, 26, 39, 52, 78 a n d 156$ .

Factors of $165 = 1, 3, 5, 11, 15, 33, 55 a n d 165$ .

Therefore, the common factor of $156$ and $165 = 1, 3$ .

Greatest common factor (G.C.F) of $156$ and $165 = 3$ .

No, $1$ is not the greatest common factor (G.C.F) of $156$ and $165$ .

Example 3: What is the sum of the prime factors of $156$ ?

Solution: To find the sum of the prime factors of $156$ , we will first look at the factors of $156$ .

Factors of $156 = 1, 2, 3, 4, 6, 12, 13, 26, 39, 52, 78 a n d 156$

Of these numbers, the ones that are only divisible by $1$ and themselves are $2, 3 a n d 13$ . Thus, the prime factors of $156$ are $2, 3 a n d 13$ . The last step is to add these up.

$S u m = 2 + 3 + 13 = 18$

We get that the sum of the prime factors of $156$ is $18$ .

Practise Question

1. What is the greatest common factor (G.C.F) of $156$ and $157$ ?

2. How many factors of $156$ are there?

3. Find the common factor of $156$ and $39$ ?

Answer

1. $1$

2. $12$

3. $1, 3, 13, 39$

Conclusion

The factors of the number $156$ are $1, 2, 3, 4, 6, 12, 13, 26, 39, 52, 78 a n d 156$ .

The prime factorization of the number $156$ is $2 \times 2 \times 3 \times 13$ or $2^{2} \times 3 \times 13$ .

FAQs on Factors of 156

1. Find the first ten multiples of $156$ .

When $156$ is multiplied by an integer, the result is a multiple of $156$ . Let's multiply from $1$ to $10$ to find the first $10$ times $156$ :

$156 \times 1 = 156$

$156 \times 2 = 312$

$156 \times 3 = 468$

$156 \times 4 = 624$

$156 \times 5 = 780$

$156 \times 6 = 936$

$156 \times 7 = 1092$

$156 \times 8 = 1248$

$156 \times 9 = 1404$

$156 \times 10 = 1560$

Therefore, the first ten multiples of $156$ are $156, 312, 468, 624, 780, 936, 1092, 1248, 1404$ , and $1560$ .

2. Find the greatest common factor of $156$ and $52$ .

The first step in determining the GCF of $156$ and $52$ is to list the factors of each number.

The factors of $156$ : $1, 2, 3, 4, 6, 12, 13, 26, 39, 52, 78 a n d 156$ itself.

The factors of $52$ : 1,2,4,13,26, and 52 itself.

Therefore, we can conclude that $52$ is the greatest common factor or divisor among all of them because it is the largest number that divides equally into each.

3. Is $156$ a composite number or a prime number?

Actually, the number $156$ is composite. The total factors for the $156$ are $12$ : $1, 2, 3, 4, 6, 12, 13, 26, 39, 52, 78 a n d 156$ . Given what we already know, a prime number only has one factor—the number itself—and is referred to as a prime number. Composite numbers, on the other hand, have more than these two factors. Although $156$ is not a perfect square and prime number.