An average is a number that is selected to represent a list of numbers in everyday life; it is frequently the sum of the numbers divided by the number of numbers in the list the arithmetic mean. For example, 5 is the average of the numbers 2, 3, 4, 7, and 9, which add up to 25. Depending on the circumstance, an average could also be another statistic like the median or mode.
What is Average in Math:
The mean value, which is the definition of the average, is the ratio of the sum of the values in a certain set to all of the values in the set. The average is essentially the mean of the variables that are represented by x. It is also denoted by the sign "μ".
Average
Formula of Average in Maths:
It is fairly simple to calculate the average of a set of numbers or values. The only thing left to do is to add up all the numbers and divide the total by the number of values provided. As a result, the following is the average formula with example:
Average: Sum of Values obtained/ Total Number of Values
Assume that we have provided n different values, such as \[{\rm{x_1}}\],\[{\rm{x_2}}\] ,\[{\rm{x_3}}\]………\[{\rm{x_a}}\].
Following data will have the average as:
Average equals \[\frac{{[{\rm{x_1}} + {\rm{x_2}}...... + {\rm{x_a]}}}}{{\rm{a}}}\]
How to Calculate Average in Maths?
Find Sum of Numbers in Step 1:
Finding the total of all the given numbers is the first step in calculating the average of a set of numbers.
Find Number of observations in Step 2:
The next step is to determine how many numbers are there in the dataset.
Calculating the Average in Step 3:
In order to arrive at the average, divide the total by the number of observations.
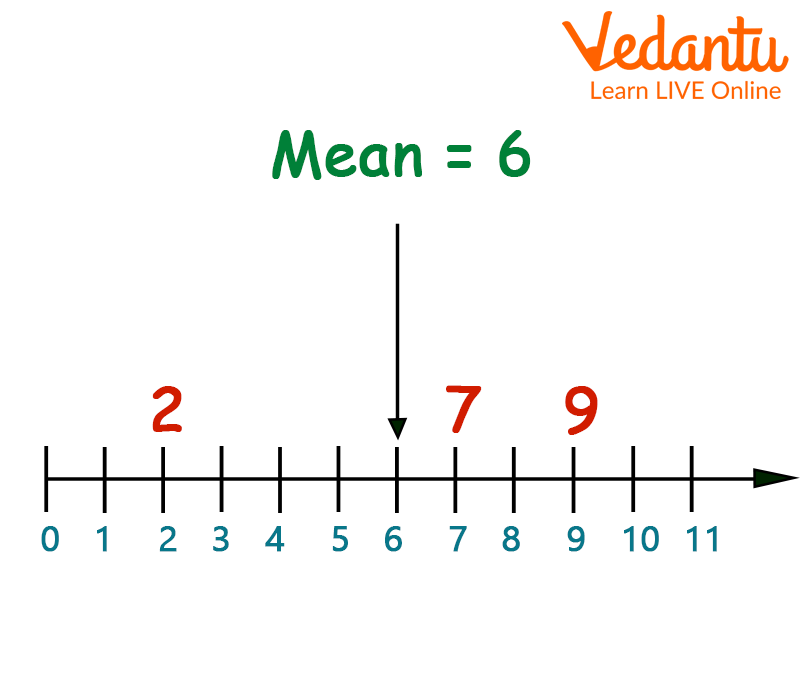
Average of 2,7,9.
Solved Average Examples:
Example 1: In a group of men with heights of 5.5, 5.3, 5.7, 5.9, 6, 5.10, 5.8, 5.6, 5.4, and 6. then measure the average height.
Ans:
Men's heights are as follows: 5.5, 5.3, 5.7, 5.9, 6, 5.10, 5.8, 5.6, 5.4, and 6.
Average is calculated as the sum of all males' heights divided by the total number of males.
A \[ = \frac{{[5.5 + 5.3 + 5.7 + 5.9 + 6 + 5.10 + 5.8 + 5.6 + 5.4 + 6]}}{{10}}\]
A \[ = \frac{{5.63}}{{10}}\]
A \[ = 5.63\]
Therefore , the average height is 5.63 units.
Example 2: If a team of nine students has members that are 12, 13, 11, 12, 13, 12, 11, 12, 12 Then determine the team's average student age.
Ans:
Given that kids range in age from 12, 13, 11, 12, 13, 12, 11, and 12,
Average: Students' combined ages divided by the total number of students
A \[ = \frac{{[12 + 13 + 11 + 12 + 13 + 12 + 11 + 12 + 12]}}{9}\]
A \[ = \frac{{108}}{9}\]
A \[ = 12\]
Consequently, a team's average age of students is 12 years old.
Example 3: Find the average of the first ten natural numbers.
Ans: As we know, the first ten natural numbers are 1,2,3,4,5,6,7,8,9,10.
Average \[ = \frac{{1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10}}{{10}}\]
\[ = \frac{{55}}{{10}}\]
\[ = 5.5\]
Thus,Average \[ = 5.5\]
Conclusion
We have seen the average chapter in maths. The mean value, which is the definition of the average, is the ratio of the sum of the values in a certain set to all of the values in the set.In everyday life, a single number is chosen to stand in for a group of other numbers.
FAQs on Average
1. How do I calculate the average and why is the average important?
The average of a set of numbers can be calculated by finding the sum of the numbers divided by the total number of values (n) in the set. For example, suppose we want to find the average of 1, 5, 4, 7, and 13. We simply find the sum of the numbers: 1 + 5 + 4 + 7 + 13 = 30, and as there are five numbers, we divide 30 by 5 to get 6. Average can be easily calculated using the average calculator.
Average is important because:
Average helps us to summarize a large amount of data into a single value.
Average indicates some variability around any single value within the original data.
2. Why do we calculate the average and what do you mean by average?
The term average is generally used frequently in everyday life to express an amount that is typical for a group of people or a group of things. Averages are useful because they summarize a large amount of data into a single value.
Average indicates that there is some variability around this single value within the original data.
We can easily calculate the average using the average calculator. The result that we get when we add two or more numbers together and divide the sum by the total number of terms is known as average. For example, suppose we want to find the average of 1, 6, 3, and 2. We simply find the sum of the numbers: 1 + 6 + 3 + 2 = 12, and as there are four numbers (n = 4), we divide 12 by 4 to get 3.
3. What are the advantages of average?
It is Fast and easy to calculate.
Sensitive to extreme value.
4. Does Averages only in mathematics?
The averages are also used in the statistics and various companies and institutes to determine the values on which decisions are made.
5. What purposes do averages serve?
Averages are used to condense a vast number of data points into a single value. It is a visual depiction of all the data set's available numbers.
6. Does the mean mean the most?
You are probably most familiar with the mean [sometimes known as the average], but there are additional central tendency measures, including the median and the mode.
