Factors of 132

When we discuss the factor of 132, we truly mean all the positive and negative integers that can be divided into 132 with zero remainder. The result of taking the number 132 and dividing it by one of its factors would be another factor of 132.

Let's examine how to identify and list each of the 132 elements.

These numbers can be written as either individual factors or factor pairs. We present them both in this case. This is a specific number's mathematical decomposition.

How to Find Factors of 132?

First, we will divide 132 by the smallest prime number, 2. Then we will find the smallest prime that divides the quotient evenly. The process will continue until we get a quotient equal to 1. In this situation, the factors are 1, 2, 3, 4, 6, 11, 12, 22, 33, 44, 66, 132, and the negatives -1, -2, -3, -4, -6, -11, -12, -22, -44, -66, -132 all of which can exactly divide 132. Factors are numbers that divide without leaving any remainder.

Prime Factors of 132

Sometimes, the prime factors of 132 and the prime factorisation of 132 are used interchangeably, which is strictly incorrect. Read this section carefully to understand the difference between the prime factors of 132 and the prime factorisation of 132.

The prime factorisation of 132 is 2 x 2 x 3 x 11. This is a simple and unique list of prime factors of 132, together with their multiplicities. 132 = 2 x 2 x 3 x 11.

The prime factors of 132 are the prime numbers that divide 132 exactly, with a remainder or modulo 0, in terms of Euclidean division.

2, 3, and 11 are the prime factors of 132.

The prime factorisation does not include 1, but it does include every copy of every prime factor. Now you know the decomposition of 132.

How to Find Prime Factors of a Number?

The prime factorisation can be done by two methods:

1. Division

2. Factor tree

The Division Method

The steps for determining the factors of any number are the same as those for determining the prime factors of that number.

• To discover the number's smallest prime factor, divide it by the smallest prime number, 2, then by 3, then by 5, and so on.

• Divide the quotient once again by the smallest prime.

• Continue doing so until, after further division, the quotient equals 1.

• Last but not least, show the number as the sum of all the prime components.

\[2 \times 2 \times 3 \times 11\] is the prime factorisation of 132. A composite number, 132. Composite numbers like 132 have at least two factorisations, in contrast to prime numbers, which only have one.

What is a Factor Tree?

A factor tree is a graphic representation of the possible factors of a number and its sub-factors. It is intended to make factorisation simpler. It is made by first determining the factors of a number and then the factors of the original number.

Once you get a large number of prime factors, which is the prime factorisation of the original number, the process recursively continues. Make sure to keep in mind the second component in a factor pair when building the tree. Now, see below the factor tree of 132.

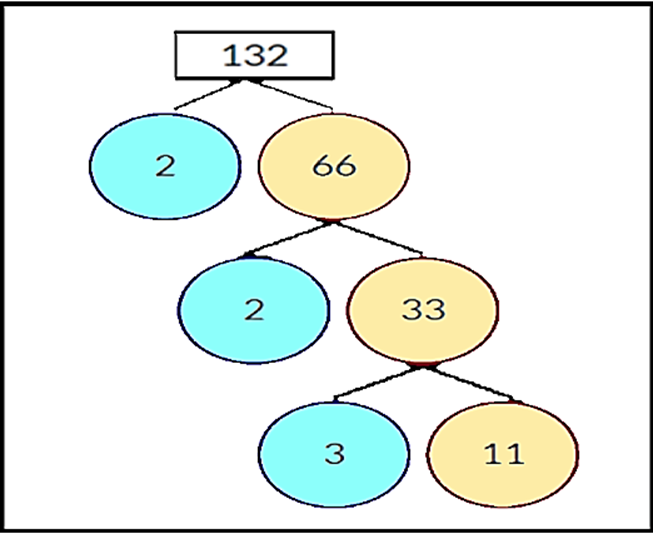
Factor tree of 132

Finding the Factors of a Number

The following steps can be used to determine how many factors there are in a given number.

• First, factor the provided number into primes, or describe it as the product of primes.

• Write the prime factorisation in exponent form.

• Increase each exponent by one.

• Multiply each of the results. This product displays how many factors there are in the given integer.

Number of Factors of 132

We know that if a number can be expressed as a product of prime numbers, then by using the power of the prime factor, we can find the number of factors of that number.

Suppose \[N = X^{a}Y^{b}Z^{c}\], where X, Y, and Z are prime factors of N.

The number of factors of N is (a+1)(b+1)(c+1).

The prime factorization of 132 is \[132 = 2 x 2 x 3 x 11 = 2^{2} x 3 x 11\].

So the number of factors of 132 is \[(2+1)(1+1)(1+1) = 3 x 2 x 2 =12\].

The number of positive factors of 132 is 12.

Solved Examples

Example 1: Find the common factors of 132 and 151.

Sol: 1, 2, 3, 4, 6, 11, 12, 22, 33, 44, 66, and 132 are the factors of 132.

The factors 151 are 1 and 151.

As 151 is a prime number, the common factor of 132 and 151 is 1.

Example 2: What are the common factors of 132 and 143?

Sol: 132 factors are 1, 2, 3, 4, 6, 11, 12, 22, 33, 44, 66, and 132.

1, 11, 13, and 143 are 143 factors.

Thus, the common factors of 132 and 143 are 1 and 11.

Example 3: Find the 132 and 66 common factors.

Sol: 1, 2, 3, 4, 6, 11, 12, 22, 33, 44, 66, and 132 are the factors of 132.

1, 2, 3, 6, 11, 22, and 66 are the factors of 66.

Therefore, 1, 2, 3, 6, 11, 22, and 66 are the common factors of 132 and 66.

Conclusion

Despite being closely related, the terms "factors," "prime factors," and "prime factorisation of 132" have different meanings and cannot, strictly speaking, be used interchangeably.

A hundred and thirty-two has the following factors: 132, 66, 44, 33, 22, 12, 11, 6, 4, 3, 2, 1 and negatives of all these factors. The first three prime factors of 132 are 2, 3, and 11. Additionally, the prime factorisation of 132 is 2 x 2 x 3 x 11. A prime factor of 132 is not 1, so keep that in mind.

Key Features

• 132 is not a prime number but a composite number, and it can be written as the product of prime numbers:

• The prime factorisation of the composite number 132:
  132 = 2 × 2 × 3 × 11

• The factors are 1, 2, 3, 4, 6, 11, 12, 22, 33, 44, 66, 132, and the negatives -1, -2, -3, -4, -6, -11, -12, -22, -44, -66, -132 all of these can exactly divide 132

List of Related Articles

• Prime factorization

• Factors of a number

• How to find the number of factors

• Prime factor

Practice On Your Own

Q 1: Find the common factors of 142 and 132.

Ans: The common factors of 134 and 142 are 1 and 2.

Q 2: Find the common factors of 132 and 420.

Ans: The common factors of 132 and 420 are 1,2,3,4,6 and 12.