Finding the Factors of 13

The numbers that divide 13 exactly without leaving a residual are known as its factors. There are no decimals or fractions that can be factors of 13, only positive or negative numbers. The pair factors of 13, for instance, might be \[\left( 1,13 \right)\] or \[\left( -1,-13 \right)\]. The outcome of multiplying the negative pair factors is the original number. It means that the product of \[-1\] and \[-13\] is 13. The sum of the factors of 13 is \[1+13=14\]. The list of 13 factors, pair factors and prime factors, will be covered in this article using both the division technique and the prime factorisation method.

Factors of an Integer

A factor is an integer divided by the original number into equal parts without the remainder. Every number greater than one has at least two factors. The answer is another factor if a number is divided by a factor. The two factors are referred to as factor products. The product of every factor pair corresponds to the number. The first factor pair is always 1 and counts itself.

Examples:

• Factors of 29 are 1 and 29.

• Factors of 31 are 1 and 31.

What is the Factor of 13?

There are only 2 factors for prime numbers, which are 1 and itself. Therefore, the only ways to divide these integers without leaving a remainder are by 1 and the number itself. Since 13 is a prime number, it has only 2 factors. Therefore, all factors of 13 are 1 and 13.

Factors of 13 by Division Method

The numbers that divide exactly by 13 without leaving a remainder are known as the factors of 13. This implies that the factors are those numbers that divide 13 exactly.

\[13\div 1=13\]

\[13\div 13=1\]

We can see that the number 13 is divisible by 1 and 13. As a result, all of these integers are called the factors of 13.

13 Prime Factorisation

The term "prime factorisation" refers to representing a number as the product of its prime factors. 13 is a prime number, which means it has only 2 factors. We know that the factors of 13 are 1 and 13. Thus, the prime factorisation of 13 is \[1\times 13\].

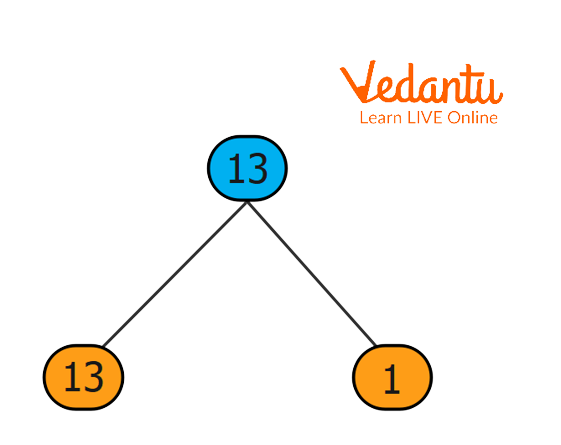
13 Prime Factorisation

Factors Pairs of 13

A pair of integers that when multiplied together results in the product value of 13 is the pair factor of 13. Both a positive and a negative pair can be represented by the pair factor of 13. 13 only has one pair factor because it is a prime number. The following is a list of the 13 pair factor values:

In pairs, the factors of 13 are \[\left( 1,13 \right)\]

and \[\left( -1,-13 \right)\].

Interesting Facts

• 13 isn't a perfect square number. The square of 13 is 169.

• 13 is both the lowest multiple and the biggest factor of 13.

• A prime number and a composite number have a common factor, which is 1.

Solved Important Questions

1. Find out the common factors of 13 and 31.

Solution: A factor is an integer that is divided by the original number into equal parts without the remainder. A number that divides each of the provided numbers perfectly is a common factor of two or more numbers. Hence, factors of 13 and 31 are 1 and 13 and 1 and 31, respectively. Therefore, the common factor of 13 and 31 is 1.

2. Find the product of all the factors of 13.

Solution: We know that the factors of 13 are 1 and 13.

The product of the factors is \[1\times 13=13\].

3. Is 3 a factor of 13?

Solution: We know that 13 is a prime number, which means it has only 2 factors. Therefore, the factors of 13 are 1 and 13. So, 3 is not a factor of 13.

Practice Questions

1. Is 13 a perfect square?

1. Yes

2. No

Ans: A

2. By which number is 13 divisible?

1. 3

2. 6

3. 13

4. 9

Ans: C

Conclusion

This article summarises the prime factorisation of 13, all factors of 13 and pair factors of 13. We know that the factors of 13 are 1 and 13 and the prime factorisation of 13 is $1\text{ }\times \text{ }13$ where 13 is a prime number. The positive and negative pair factors are $\left( 1,\text{ }13 \right)$ and $\left( -1,\text{ }-13 \right)$, respectively.