




How to Identify Equal Chords and Calculate Their Distances
Well, we see many round objects in daily life like coins, clocks, wheels, bangles, and many more. In this article, we will learn about the equal chords theorem i.e. the equal chords of a circle are equidistant from the center of the circle. And then will learn its converse too. After that, we discussed the theorem regarding the intersection of equal chords. At last, we will learn the diameter is the largest chord of the circle and we will solve examples to understand the concepts more easily.
Perpendicular Bisector of a chord
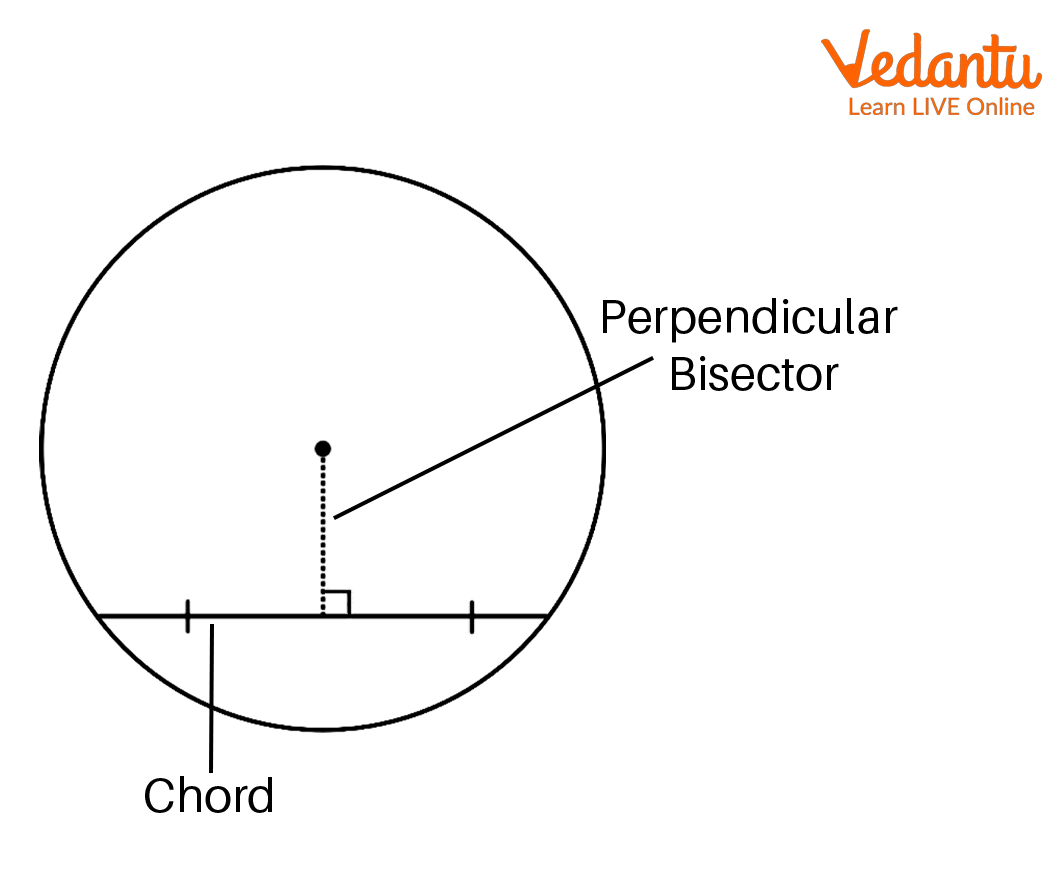
Perpendicular Bisector of the Chord
Here, two points are joined to form a line segment which we call as Chord of the circle. The longest chord of a circle is called the diameter. When a line crosses the line at \[{90^ \circ }\](perpendicular) and cuts in half (bisector) is called the perpendicular bisector of the chord. Also, this perpendicular bisector of the chord passes through the center of the circle. To represent a perpendicular line is ‘\[ \bot \]’. Thus, the perpendicular drawn from the center of a circle to a chord bisects the chord.
Chords and their Distance from the Center
As we know that there are infinite numbers of points on a line segment. We take a circle with center O having chord AB as shown below:

Chord and their Distance from the Center
Next, to find the distance between the chord and the center O, if we join the infinite points on the line segment AB with O then we will get infinite line segments of different lengths. As we can see, line ON is perpendicular to AB and it has the shortest length i.e. \[ON \bot AB\]. This means the shortest length ON is the distance between O and AB. Thus we can say that the length of a perpendicular from a point to a line is the distance between the point from the line.
Equal Chords and their Distance from the Center Theorem
Statement: Equal chords of a circle (or of congruent circles) are equidistant from the center (or centers).
Given: We have a circle with center O. AB and CD are chords that are equal i.e. AB = CD. Also, OX and OY are perpendiculars to AB and CD respectively
To prove: OX = OY

Equal Chords and their Distance from the Center Theorem
Proof:
Draw OA and OC as shown in the figure.
As we know, perpendicular from the center to the chord bisects the chord.
Since, \[OX \bot AB\]
\[ \Rightarrow AX = BX = \frac{{AB}}{2}\] -------- (1)
Similarly for \[OY \bot CD\]
\[ \Rightarrow CY = DY = \frac{{CD}}{2}\] ---------- (2)
Next, given that AB = CD
\[ \Rightarrow \frac{{AB}}{2} = \frac{{CD}}{2}\]
Using equations (1) and (2), we will get,
\[ \Rightarrow AX = CY\] -------- (3)
In \[\Delta AOX\] and \[\Delta COY\],
As both are right-angled triangles i.e. \[{90^ \circ }\]
\[ \Rightarrow \angle OXA = \angle OYC\]
\[ \Rightarrow OA = OC\] (Both are the radii of the circle)
\[ \Rightarrow AX = CY\] (From (1))
So, RHS rule we can say that, \[\Delta AOX \cong \Delta COY\]
\[ \Rightarrow OX = OY\] (From CPCT rule)
Hence it is proved that equal chords of a circle are equidistant from the center.
The Converse of this Above Theorem
Statement: Chords equidistant from the center of a circle are equal in length.
Given: We have a circle with center O. Also, AB and CD are chords of the circle where OX and OY are the distances from the center i.e. \[OX \bot AB\] (\[AX = BX = \frac{{AB}}{2}\]) and \[OY \bot CD\] (\[CY = DY = \frac{{CD}}{2}\]) respectively. And, OX = OY.
To prove: The chords are equal i.e. AB = CD

Converse of Equal Chords and their Distance from the Center Theorem
Proof:
Draw OA and OC as shown in the figure.
In \[\Delta AOX\] and \[\Delta COY\]
As both are right-angled triangles i.e. \[{90^ \circ }\]
\[ \Rightarrow \angle OXA = \angle OYC\]
\[ \Rightarrow OA = OC\] (Both are the radii of the circle)
\[ \Rightarrow OX = OY\] (Given)
So, from RHS rule we can say that, \[\Delta AOX \cong \Delta COY\]
\[ \Rightarrow AX = CY\] (From CPCT rule) ------- (1)
Next, perpendiculars from the center to the chord bisect the chord of the circle.
So, for the chord AB:
\[\therefore \] \[OX \bot AB\]
\[ \Rightarrow \] X bisects AB
\[ \Rightarrow AX = BX = \frac{{AB}}{2}\] ------ (2)
And, for the chord CD:
\[\therefore \]\[OY \bot CD\]
\[ \Rightarrow \] Y bisects CD
\[ \Rightarrow CY = DY = \frac{{CD}}{2}\] ------ (3)
Lastly, from (1), we have:
\[\therefore AX = CY\]
\[ \Rightarrow \frac{{AB}}{2} = \frac{{CD}}{2}\] (From (2) and (3))
\[ \Rightarrow AB = CD\]
Hence it is proven.
The Intersection of Equal Chords
Statement: If two equal chords of a circle intersect within the circle. Prove that, the segments of one chord are equal to the corresponding segments of another chord.
Given: AB = CD and both the chords intersect at point E in the circle.
To prove: AE = ED and CE = BE

The Intersection of Equal Chords
Proof:
First, join points O and E.
Then, draw a line OM from the center to the chord AB.
\[ \Rightarrow OM \bot AB\]
\[ \Rightarrow \]M bisects AB, which means M is the midpoint on AB.
\[ \Rightarrow AM = MB\] ---------------- (1)
Similarly, draw a line ON from the center to the chord CD.
\[ \Rightarrow ON \bot CD\]
\[ \Rightarrow \]N bisects CD, which means N is the midpoint on CD.
\[ \Rightarrow CN = ND\] ----------------- (2)
Now, we will see the proof:
As we have given AB = CD
\[ \Rightarrow \frac{1}{2}AB = \frac{1}{2}CD\]
\[ \Rightarrow AM = ND\]
\[ \Rightarrow MB = CN\]
\[ \Rightarrow MB = AM = ND = CN\] ------------------- (3)
In \[\Delta OME\] and \[\Delta ONE\]
\[ \Rightarrow \angle OME = \angle ONE = {90^ \circ }\] ( By construction)
\[ \Rightarrow OE = OE\] (Common side)
As the distance from the center is equal if the chords (AB=CD) are equal, we have
\[ \Rightarrow OM = ON\]
\[\therefore \Delta OME \cong \Delta ONE\] (RHS rule)
\[ \Rightarrow ME = EN\] ( CPCT rule) ----- (4)
Next, from (1) and (3), we will get,
\[ \Rightarrow AM = ND\]
Add (4) on both sides, we will get,
\[ \Rightarrow AM + ME = EN + ND\]
\[ \Rightarrow AE = DE\] ---------- (5)
And, subtract (5) from AB=CD
\[ \Rightarrow AB - AE = CD - DE\]
\[ \Rightarrow BE = CE\]
Hence, it is proven.
Interesting Facts
The radius of the circle bisects the chord at \[{90^ \circ }\].
When two radii join the two ends of a chord, they form an isosceles triangle.
The converse of intersecting equal chords: Two intersecting chords of a circle make equal angles with the diameter that passes through their point of intersection then the chords are equal.
When a line is drawn through the center of a circle that bisects the chord is perpendicular to the chord.
Important Questions
1. A circular road of radius 20m. Three girls A, S and D are sitting at equal distances on its boundary, each having a toy telephone in their hands to talk to each other. Find the length of the string of each phone.
Solution:
We are given that, OS = 20m and AS = SD = DA =?
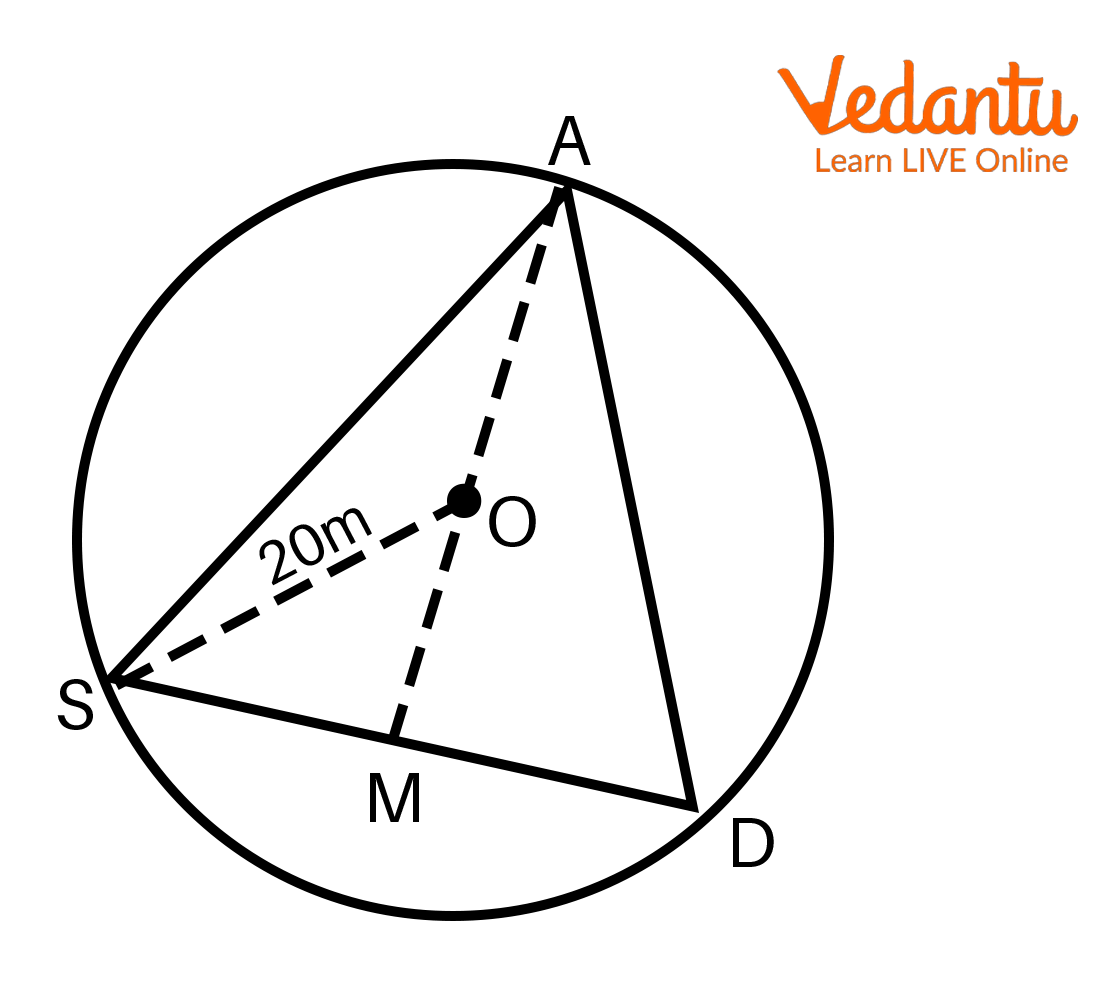
Circular Road of Radius 20 m
From this, we can say that \[\Delta ASD\] is an equilateral triangle.
\[ \Rightarrow OS = OA = OD = 20\]
As AM is the median and altitude of \[\Delta ASD\]
\[ \Rightarrow \]M is the midpoint of SD --------- (1)
And point O is the centroid.
\[\therefore \]O divides AM in 2:1
\[ \Rightarrow \frac{{OA}}{{OM}} = \frac{2}{1}\]
\[ \Rightarrow \frac{{20}}{{OM}} = \frac{2}{1}\]
\[ \Rightarrow OM = 10m\]
Next, from this we can see that \[\Delta OMS = {90^ \circ }\]
\[ \Rightarrow O{S^2} = O{M^2} + S{M^2}\]
\[ \Rightarrow {(20)^2} = {(10)^2} + S{M^2}\]
\[ \Rightarrow S{M^2} = 300\]
\[ \Rightarrow SM = 10\sqrt 3 m\]
From (1) we can say that,
\[ \Rightarrow SM = DM = 10\sqrt 3 m\]
\[ \Rightarrow SD = 2SM = 2 \times 10\sqrt 3 \]
\[ \Rightarrow SD = 20\sqrt 3 \]m
Thus, we have \[AS = SD = AD = 20\sqrt 3 \]m.
2. In this circle with center O, the radius is 8 cm and XY=PQ=12 cm. Find the lengths of OS and OT.
Solution:
According to the given information, we will get,

A Perpendicular on the Chord
Given: OY=OQ=8 cm ------- (1)
And, XY = 12 cm
According to the figure,
\[ \Rightarrow XS + SY = SY\]
Also, the perpendicular drawn from the center to the chord bisects the chord
\[ \Rightarrow XS = SY\]
Next, \[SY + SY = XY\]
\[ \Rightarrow SY = \frac{1}{2} \times XY\]
\[ \Rightarrow SY = \frac{1}{2} \times 12\]
\[ \Rightarrow SY = 6\] cm ----- (2)
In \[\Delta OSY\], using Pythagoras Theorem,
\[ \Rightarrow O{Y^2} = S{Y^2} + O{S^2}\]
\[ \Rightarrow O{S^2} = O{Y^2} - S{Y^2}\]
\[ \Rightarrow O{S^2} = {8^2} - {6^2}\]
\[ \Rightarrow O{S^2} = 28\]
\[ \Rightarrow OS = 2\sqrt 7 \]cm -------- (3)
According to the question, XY=PQ
\[ \Rightarrow OS = OT\] ( Equal chords of a circle are equidistant from the center)
\[ \Rightarrow OT = 2\sqrt 7 \] cm -------- (4)
Thus, the length of OS and OT is \[2\sqrt 7 \] cm.
3. If a line intersects two concentric circles (circles with the same center) with center O at A, B, C and D. Prove that AB = CD.
Solution:
We have taken point E which joins from the center. According to the given information, we get the following figure:

Two concentric circles
As \[OE \bot AD\]
\[ \Rightarrow AE = ED\] ----- (1)
And, \[OE \bot BC\]
\[ \Rightarrow BE = EC\] ----- (2)
From (1) – (2), we will get,
\[ \Rightarrow AE - BE = ED - EC\]
\[ \Rightarrow AB = CD\]
Thus, it is proved.
Conclusion
The article summarizes the theorem of equal chords and their distances from the center i.e. equal chords are equidistant from the center and then it's converse too. Then we learned the theorem of the intersection of equal chords too. Also, this article has solved examples to understand the concepts easily and see that the largest chord of the circle is known as the diameter.
Practice Questions
1. We have two circles of radii 5 cm and 3 cm which intersect at two points and the distance between their centers is 4 cm. Find the length of the common chord.
A. 3 cm
B. 6 cm
C. 4 cm
2. Equal chords of a circle make equal angles at the center of a circle. Is this statement true?
A. Yes
B. No
C. Can’t determined
Answers:
1) B
2) A
FAQs on Equal Chords and Their Distances from the Centre
1. What is the relationship between equal chords and their distance from the center of a circle?
The core relationship is defined by a key theorem in geometry: Equal chords of a circle are equidistant from the center. This means if you have two or more chords within the same circle that have the exact same length, the perpendicular distance from the center of the circle to each of these chords will be identical.
2. What can be said about two chords in a circle that are equidistant from the center?
This is the converse of the main theorem. If two chords in a circle are equidistant (at the same perpendicular distance) from the center, then the chords must be equal in length. This principle works both ways and is fundamental to solving many problems related to circles as per the CBSE 2025-26 syllabus.
3. How does the length of a chord change as it moves closer to the center of a circle?
As a chord moves closer to the center of a circle, its length increases. The longest possible chord in any circle is the diameter, which passes directly through the center. Conversely, the farther a chord is from the center, the shorter its length becomes.
4. Is a radius of a circle considered a chord? Explain why or why not.
No, a radius is not a chord. A chord is defined as a line segment whose two endpoints both lie on the circumference of the circle. A radius, on the other hand, is a line segment that connects the center of the circle to a single point on the circumference. Therefore, it does not meet the definition of a chord.
5. Do equal chords of a circle subtend equal angles at the center?
Yes, this is another important theorem related to chords. Equal chords of a circle subtend equal angles at the center. If you draw lines from the endpoints of two equal chords to the center of the circle, the two triangles formed will be congruent (by SSS congruence criterion), and thus the angles at the center must be equal.
6. How do you calculate the distance of a chord from the center using its length and the circle's radius?
You can calculate this distance using the Pythagorean theorem. The process involves these steps:
- Draw a perpendicular line from the center to the chord. This line represents the distance you want to find.
- This perpendicular line bisects the chord, dividing it into two equal halves.
- A right-angled triangle is formed with the radius as the hypotenuse, half the chord's length as one side, and the distance from the center as the other side.
- Apply the Pythagorean theorem: (Radius)² = (Distance)² + (½ Chord Length)². You can then solve for the distance.
7. If two chords are not equal, what can we infer about their distances from the center?
If two chords are unequal in length, we can infer that they are at unequal distances from the center. Specifically, the longer chord is closer to the center, and the shorter chord is farther from the center. This is a direct consequence of the relationship between a chord's length and its proximity to the circle's center.
8. Why does the perpendicular from the center to a chord bisect it, and how is this principle used in theorems about equal chords?
The perpendicular from the center bisects a chord because it creates two congruent right-angled triangles. When you draw the perpendicular and connect the radii to the chord's endpoints, you get two triangles sharing a common side (the perpendicular distance) and having equal hypotenuses (the radii). By the RHS (Right-angle-Hypotenuse-Side) congruence rule, the triangles are congruent, proving the chord is bisected. This principle is crucial for proving theorems about equal chords because it allows us to use the Pythagorean theorem to create a direct mathematical link between a chord's length and its distance from the center.
9. Can you provide a real-world analogy to understand why chords closer to the center are longer?
Imagine a large, circular pizza. The diameter is the longest possible straight cut you can make, and it passes through the exact center. If you make other straight cuts (chords) across the pizza, you'll notice that the cuts made closer to the center are much longer than the small cuts you might make near the edge. This provides a simple, visual analogy for the geometric principle that chords nearer to the center are always longer.






























