




How to Find the Center of a Circle With Examples
A circle, in particular, is a simple closed curve that splits the plane into two areas: interior and exterior. In common usage, the term "circle" can refer either to the figure's boundary or the entire figure, including its interior; in strict technical everyday language, the circle is only the border, and the entire figure is called a disc. The center of a circle is the point where all the lines that form the boundary meet. The origin of circle is a point from which all distances to it are measured. In this article, we will be exploring origin of circle and its implications.

Center of a Circle
What is the Center of a Circle?
The point inside a circle that is equally spaced from all other points on the circle is considered the center of a circle.
It is a point inside the circle which is at an equal distance from all the points on its circumference.
The center of a circle is often referred to as the origin of a circle.
A circle's radius-The radius of a circle is the distance between the circle's center and any point on its circumference.
It is usually represented by the letters 'R' or 'r'.
A circle's diameter- The diameter is the length of the line passing through the center and touching two points on the circle's boundary.
A Circle's Chord-A straight line joining two points on the circumference of the circle is the chord of the circle.
The diameter of a circle is defined as the circle's longest chord.
How to Find the Center of a Circle?
Following is the method to find the origin of a circle by drawing chords.
1. Draw a chord in a circle (ab)

Chord in a Circle
2. Draw another chord parallel to the previous chord (XY)
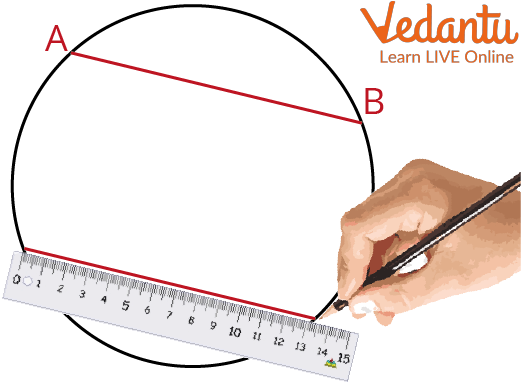
Another Chord
3. Join points a and y Using a ruler
4. Join points b and x Using a ruler
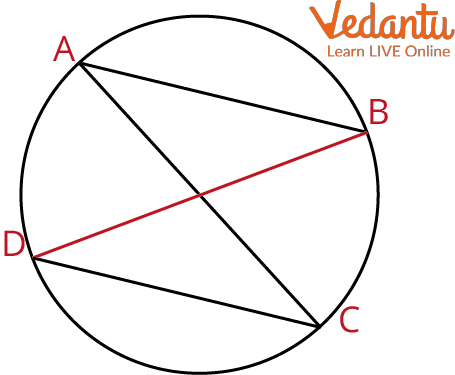
Join the Points
5. The point where the lines intersect is the center of the circle.
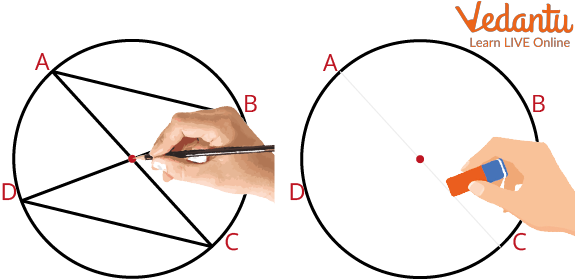
The Lines Intersecting is the Center of the Circle
Solved Example
Example 1: Find the area of a circle whose radius is 28 cm.
Ans: Given,
Radius of circular region = r = 28 cm
Area of a circle = $\pi\,r^2$
= $\dfrac{22}{7}\times 28 \times 28$
= $22\times 4\times21$
= 1848 sq. cm
Therefore, the area of the circular region is 1848 sq. cm.
Example 2: Tell whether the given statement is true or not: If the endpoints of the diameter of the circle are given, then to find the coordinates of the center we use the mid-point formula.
Ans: True, if the endpoints of the circle's diameter are given, then to find the coordinates of the center we use the mid-point formula.
Practice Questions
Q1. Find the diameter of a circle whose radius is 10 cm.
Ans: 20cm
Q2. The radius of a circle is 2 cm. What is the diameter of a circle whose radius is 3 times that of the given circle?
Ans: 12cm
Summary
So, from the article, we know that a circle is made up of all points in the same plane that are equidistant from one another. The center of a circle is the point equidistant from all points on the edge of the circle. It is also the point at which the circle's circumference (the line that defines the edge of the circle) intersects its diameter (the distance across the circle). The center of a circle is important in geometry because it is used to define many other geometric concepts, such as radius, chord, and arc.
FAQs on Center of a Circle: Definition & Formula
1. What is the center of a circle?
The center of a circle is a fixed point inside the circle that is equally distant from every point on the circumference. This point is crucial for defining the circle and calculating measurements like the radius and diameter.
2. How do you find the center of a circle given its equation?
To find the center of a circle from its equation in standard form, $(x - h)^2 + (y - k)^2 = r^2$, the center is at the point $(h, k)$, where $h$ and $k$ are the coordinates for the center.
3. What is the significance of the center in a circle?
The center of a circle is significant because it determines all main properties of a circle, including:
- Radius
- Diameter
- Symmetry
4. Can you construct the center of a circle using a compass and straightedge?
Yes, you can find the center of a circle by drawing two different chords, creating perpendicular bisectors for both, and marking their intersection point, which will be the center. This geometric method works for any size circle.
5. How does the center relate to the radius of the circle?
The radius is the constant distance from the center of the circle to any point on the circumference. Knowing the center is essential to measure or draw the radius accurately, as every radius must start from the center.
6. In coordinate geometry, how is the center of a circle represented?
In coordinate geometry, the center of a circle is represented by coordinates $(h, k)$, where $h$ is the x-coordinate and $k$ is the y-coordinate. These values specify the exact center of the circle on a Cartesian plane.
7. What is the formula for the equation of a circle using its center?
The standard equation of a circle with center $(h, k)$ and radius $r$ is: $$(x - h)^2 + (y - k)^2 = r^2.$$ This formula uniquely defines the circle and its center on a coordinate plane.
8. Why is the center of a circle important in real-life applications?
The center of a circle is important in various real-life applications, such as:
- Designing wheels and gears
- Plotting circular gardens
- Creating round tables
9. How do you identify the center of a circle on a graph?
On a graph, the center of a circle can be identified by looking at the coordinates $(h, k)$ in the equation or by finding the midpoint that is equidistant from all points along the circle’s boundary.
10. Can a circle have more than one center?
No, a circle cannot have more than one center. By definition, every circle has exactly one unique point from which all points on its circumference are equally distant. This makes the center a defining feature of a circle.
11. What is the relationship between the center of a circle and its diameter?
The diameter of a circle passes through the center of the circle and connects two points on the circumference. The length of the diameter is always twice the radius, so $d = 2r$ where $d$ is diameter and $r$ is radius.
12. How can you locate the center if only part of a circle is visible?
If only a part of a circle is visible, you can draw at least two chords within the visible section, create perpendicular bisectors for each, and their intersection point estimates the center of the circle even without the full shape.























