Question

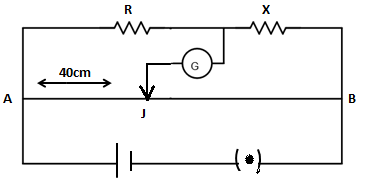
Write the principle on which the working of a meter bridge is based. In an experiment on meter bridge, a student obtains the balance point at the point J such that, as shown in figure. The values of R and X are both doubled and then interchanged. Find the new position of the balance point. If the galvanometer and battery are also interchanged how will the position of balance point be affected?

Answer 1

Hint: Meter Bridge is the simplest practical application of Wheatstone bridge. Initial balance point of Wheatstone bridge substitute in the balance equation. By doubling the value of R and X in the balance equation, a new balance point is calculated.

Complete step by step answer:
Meter bridge working is based on the principle of Wheatstone bridge. After taking out a suitable resistance R from the resistance box, the jockey is moved along the wire AB till there is no deflection in the galvanometer. This is the balance condition of the Wheatstone bridge. If P and Q are the resistance of the parts AJ and JB of the wire, then for the balanced condition of the bridge, we have
\[\dfrac{P}{Q} = \dfrac{R}{X}\]
Now, let us write the information given in the question.
Balance point\[AJ = 40cm\], now R and X are doubled and interchanged then the new balance point we have to find.
Let us use the balancing condition for Wheatstone bridge \[\dfrac{P}{Q} = \dfrac{R}{X}\]
Initial balance point is 40cm.
\[\dfrac{R}{X} = \dfrac{{40}}{{100 - 40}} = \dfrac{{40}}{{60}}.....\left( 1 \right)\]
Now, according to the question, when the vales of both the X and \[R\]are doubled and interchanged, the balance point (L) is calculated below.
$\Rightarrow$ \[\dfrac{{2X}}{{2R}} = \dfrac{L}{{100 - L}}....\left( 2 \right)\]
Let us equate equation (1) and (2).
$\Rightarrow$ \[\dfrac{{40}}{{60}} = \dfrac{L}{{100 - L}}\]
Taking cross multiplication we get,
$\Rightarrow$ \[60L = 40\left( {100 - L} \right)\]
On multiply the bracket term and we get,
\[60L = 4000 - 40L\]
Let us subtract we get,
\[ \Rightarrow L = 40cm\]
Hence, the new balancing point is the same as earlier.
If the galvanometer and battery are also interchanged there will be no effect on the position of balance point.

Note: The deflection of galvanometer not getting affected by interchanging position of battery and galvanometer. In a slide wire, if a balance point is obtained at L cm from the zero ends, then the unknown resistance X is calculated as by below expression.
$X = \dfrac{{\left( {100 - L} \right)}}{L}R$