Question

Work done for the process shown in the figure is:


(A) $1\,J$
(B) $1.5\,J$
(C) $4.5\,J$
(D) $0.3\,J$

Answer 1

Hint From the given figure, the detailed figure is drawn, then the solution can be determined. In the detailed diagram it forms one rectangle and one right angled triangle. By finding the area of the two shapes and adding the two areas is equal to the work done.
Useful formula:
The area of the rectangle is given as,
${A_r} = l \times b$
Where, ${A_r}$ is the area of the rectangle, $l$ is the length of the rectangle and $b$ is the breadth of the rectangle.
The area of the right-angled triangle is given as,
${A_t} = \dfrac{{ab}}{2}$
Where, ${A_t}$ is the area of the right angle triangle, $a$ is the base of the triangle and $b$ is the height of the triangle.

Complete step by step solution
Given that,
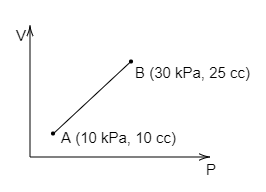
The initial condition of the volume is, ${V_1} = 10\,cc$.
The final condition of the volume is, ${V_2} = 25\,cc$.
The initial condition of the pressure is, ${P_1} = 10\,kPa$.
The final condition of the pressure is, ${P_2} = 30\,kPa$.
The work done of the process is given by the following figure.

From the above diagram, the area of the rectangle is given by,
${A_r} = l \times b$
By substituting the length and the breadth of the rectangle from the above diagram, then the above equation is written as,
${A_r} = 10 \times 15$
By multiplying the terms in the above equation, then the above equation is written as,
${A_r} = 150\,kPa.cc$
From the above diagram, the area of the triangle is given by,
${A_t} = \dfrac{{ab}}{2}$
By substituting the base and the height of the triangle from the above diagram, then the above equation is written as,
${A_t} = \dfrac{{20 \times 15}}{2}$
By multiplying the terms in the above equation, then the above equation is written as,
${A_t} = \dfrac{{300}}{2}$
By dividing the terms in the above equation, then the above equation is written as,
${A_t} = 150\,kPa.cc$
The work done is the sum of the two areas, then the work done is given as,
$W = 150 + 150$
By adding the terms in the above equation, then the above equation is written as,
$W = 300\,kPa.cc$
Then the above equation is written as,
$W = 0.3\,J$

Hence, the option (D) is the correct answer.

Note: The work done of the object is directly proportional to the force of the object and the distance between them. As the force of the object and the distance between them increases, then the work done of the object is also increasing. As the force of the object and the distance between them decreases, then the work done of the object is also decreasing.