
Which one the following has the smallest dipole moment?
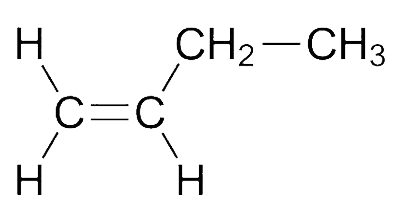
A. $1 - $Butene
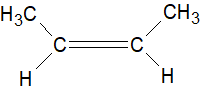
B. Cis$ - 2 - $Butene
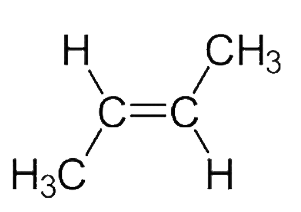
C. Trans$ - 2 - $Butene
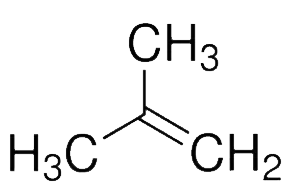
D. $2 - $methyl-propene
Answer
222k+ views
Hint: In compounds where there is visible charge separation, a dipole moment can be demonstrated. Therefore, we can assert that ionic and covalent bonding both produce the dipole moment. Dipole moments are also influenced by the different electronegativity of the two atoms that are chemically connected.
Complete Step-by-Step Explanation:
The polarity of a chemical bond formed between two atoms in a molecule is often measured by a bond dipole moment. It provides us with the idea of an electric dipole moment, which is typically used to measure the separation of the positive and negative charges in a system. Dipole moments have both a magnitude and a direction, making them vector quantities. Due to the ability of a vector quantity, it can also have the value zero since two bond dipoles with opposing charges can cancel one another out.
Dipole moment is also influenced by a compound's structural characteristics or more specifically that is by the bond angle. Bond angle is zero for symmetrical structures and has some value for asymmetrical structures.
In the given options, we notice that trans\[ - 2 - \]Butene molecule shows zero dipole moment because as there is just one ethyl group connected which is increasing the \[{e^ - }\]density on the \[C = C\], the dipole moment in \[1\] will be the smallest.
Since there are \[2C{H_3}\] groups present \[II\], being cis, has a greater dipole moment.
Due to the arrangement of the $C{H_3}$groups, the dipole moment in the option$C$, Trans$ - 2 - $Butene is $O$and to the presence of $2C{H_3}$groups on one carbon of $c = c$,
And in the option$D$, $2 - $methyl-propene exhibits the highest dipole moment.
Thus, the correct option is (C) Trans\[ - 2 - \]Butene
Note: It should be noted that the product of the charge's magnitude and the separation between the positive and negative charge centers yields the dipole moment. The Greek letter \[\mu \] is used to signify it. In mathematics, it is written as: \[\mu = Q \times r\].
Complete Step-by-Step Explanation:
The polarity of a chemical bond formed between two atoms in a molecule is often measured by a bond dipole moment. It provides us with the idea of an electric dipole moment, which is typically used to measure the separation of the positive and negative charges in a system. Dipole moments have both a magnitude and a direction, making them vector quantities. Due to the ability of a vector quantity, it can also have the value zero since two bond dipoles with opposing charges can cancel one another out.
Dipole moment is also influenced by a compound's structural characteristics or more specifically that is by the bond angle. Bond angle is zero for symmetrical structures and has some value for asymmetrical structures.
In the given options, we notice that trans\[ - 2 - \]Butene molecule shows zero dipole moment because as there is just one ethyl group connected which is increasing the \[{e^ - }\]density on the \[C = C\], the dipole moment in \[1\] will be the smallest.

Since there are \[2C{H_3}\] groups present \[II\], being cis, has a greater dipole moment.

Due to the arrangement of the $C{H_3}$groups, the dipole moment in the option$C$, Trans$ - 2 - $Butene is $O$and to the presence of $2C{H_3}$groups on one carbon of $c = c$,

And in the option$D$, $2 - $methyl-propene exhibits the highest dipole moment.

Thus, the correct option is (C) Trans\[ - 2 - \]Butene
Note: It should be noted that the product of the charge's magnitude and the separation between the positive and negative charge centers yields the dipole moment. The Greek letter \[\mu \] is used to signify it. In mathematics, it is written as: \[\mu = Q \times r\].
Recently Updated Pages
Types of Solutions in Chemistry: Explained Simply

States of Matter Chapter For JEE Main Chemistry

Know The Difference Between Fluid And Liquid

Difference Between Crystalline and Amorphous Solid: Table & Examples

Conduction Explained: Definition, Examples & Science for Students

Balancing of Redox Reactions - Important Concepts and Tips for JEE

Trending doubts
JEE Main 2026: Application Form Open, Exam Dates, Syllabus, Eligibility & Question Papers

Derivation of Equation of Trajectory Explained for Students

Hybridisation in Chemistry – Concept, Types & Applications

Understanding the Angle of Deviation in a Prism

How to Convert a Galvanometer into an Ammeter or Voltmeter

Degree of Dissociation: Meaning, Formula, Calculation & Uses

Other Pages
NCERT Solutions For Class 11 Chemistry Chapter 7 Redox Reaction

JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

Hydrocarbons Class 11 Chemistry Chapter 9 CBSE Notes - 2025-26

Thermodynamics Class 11 Chemistry Chapter 5 CBSE Notes - 2025-26

NCERT Solutions ForClass 11 Chemistry Chapter Chapter 5 Thermodynamics

Equilibrium Class 11 Chemistry Chapter 6 CBSE Notes - 2025-26




