Question

Which of the following distance time graph is representing the uniform accelerated motion of body:
A)

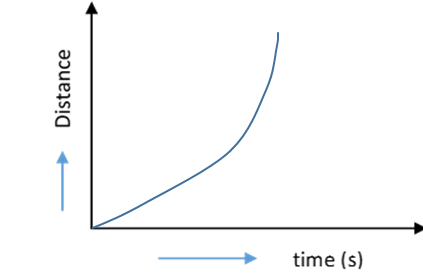
B)







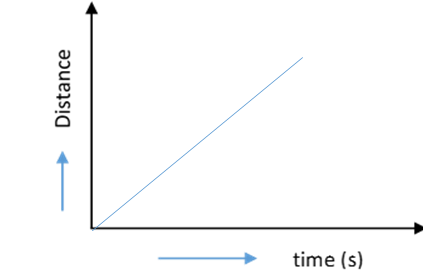
C)







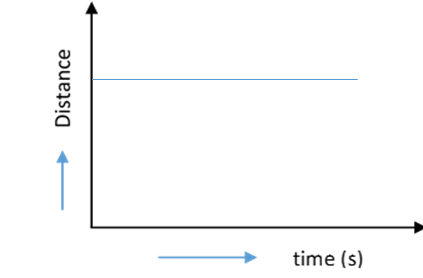
D) $\text{None of these}$

Answer 1

Hint: The distance time graph is representing the uniform accelerated motion of the body. Uniform Acceleration is derivative of v with respect to time. Here v is the velocity. When the body is provided constant acceleration, then it is uniformly accelerated motion. So, the constant external force is applied by the body, then direction of acceleration is change of velocity.

Complete step by step solution:
In accelerated motion the distance time graph is not a straight line. The graph is parabola when there is a uniform accelerated motion and Graph is irregular when there is non-uniform acceleration.
For a body to undergo an accelerated motion, the velocity time graph is a straight line. This means that the velocity will vary linearly with respect to time. However, the same is not true for displacement-time graphs. The displacement curve with respect to time will be most likely a parabolic curve. This is because the double derivative of displacement with respect to time is not zero.
Option A is correct. This is because change in distance per second is not constant. So, derivative will not be zero and uniform acceleration is performed.
Option B is incorrect. This is because change in distance per second is constant so if we take the derivative of this to get acceleration, the whole function becomes zero. Therefore, it is not representing the uniform acceleration in this case.
Option C is also incorrect. This is because distance is not changing with time so even the first derivative makes it zero. Therefore, there is no point in talking about acceleration.
When the slope of time is increasing, the velocity of the body also increases and so that the body is in accelerated motion.

Therefore, Option A is the correct answer.

Note: Velocity is the first derivative of distance with respect to time and acceleration is the second derivative of distance. So, neither displacement should be constant nor should change in displacement be constant.